Dialogiske tilgange: Samtaletræk
Dialogisk undervisning kan udvikles ved hjælp af forskellige og tilpasningsdygtige pædagogiske tilgange. Modellen ”samtaletræk” giver underviseren mulighed for at bruge forskellige måder at samtale på og inddrage eleverne.
Modellen ”samtaletræk” som støtte til dialogiske interaktioner
Modellen illustrerer forskellige aspekter af dialogisk undervisning, hvor der er fokus på, at en elevs matematiske bidrag bygger på andre elevers bidrag. Dette resulterer i en fælles udvikling af meningsfulde matematiske ideer. Modellen ”samtaletræk” kan anvendes som inspiration til at fremme dialogisk undervisning. (Kilde 1)
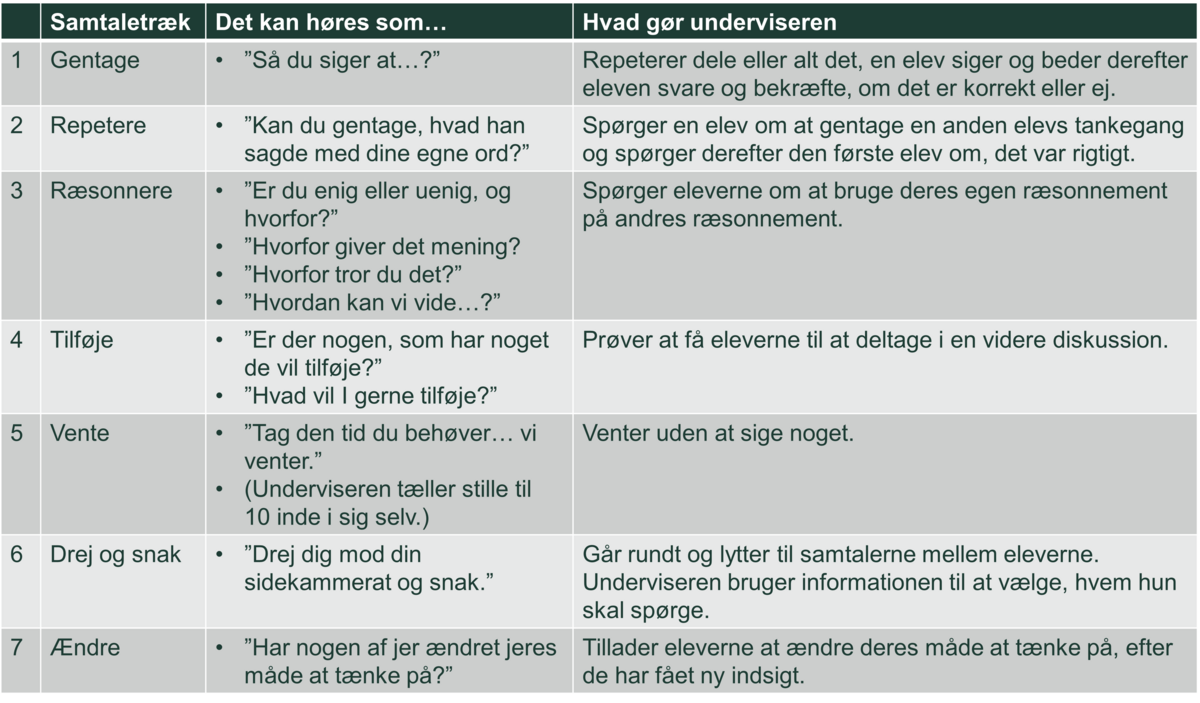
Nedenfor gives også et kort oprids af hvert samtaletræk:
Samtaletræk 1: Gentage
Nogle gange kan elever have svært ved at formulere deres tanker. Underviseren kan bruge gentagelse som et redskab til at håndtere uklarheder i elevernes forklaringer og forsøge at skabe klarhed om, hvordan eleverne tænker. Dette kan også hjælpe andre elever med at forstå en klassekammerats forklaring. Underviseren kan helt eller delvist gentage det, en elev siger, og bede eleven om at bekræfte, om det er korrekt eller ej. Samtidig får eleverne tid til at tænke, hvilket gør det lettere for dem at følge med i det matematiske indhold.
Samtaletræk 2: Repetere
Underviseren kan udvide gentagelsestrækket til også at involvere klassekammerater. Ved at spørge en elev, om vedkommende kan gentage, hvad en anden elev har sagt, og derefter straks følge op med at spørge den første elev, om de kan bekræfte det sagt, f.eks. ”Er det rigtigt? Var det det, du sagde?” Dette samtaletræk giver eleverne tid til at forstå den idé, der bliver diskuteret.
Samtaletræk 3: Ræsonnere
Efter en elev har fremsat en påstand, f.eks. at ”6 er et ulige tal” og underviseren er sikker på, at eleverne har hørt denne påstand og haft tid til at overveje den, kan hun fortsætte dialogen for at tydeliggøre, hvordan eleverne ræsonnerer omkring den. Underviseren anvender ”ræsonnere” -trækket til at udforske en påstand, f.eks.:
Underviser (U): Er du enig eller uenig i, at 6 er et ulige tal?
Elev (E): Jeg er uenig.
U: Kan du fortælle os, hvorfor du er uenig? Hvordan har du tænkt (ræsonneret)?
E: I går talte vi om, at lige tal kan deles i to lige store dele, og jeg tænker, at det kan 6, og det giver to dele med 3 i hver del. Så må det være et lige tal.
Underviseren har ikke støttet nogen af påstandene, men bruger samtaletrækket til at starte en diskussion omkring ideer. Når eleverne bedre forstår emnet, er det vigtigt, at underviseren forbinder de relevante ideer (elevernes forskellige måder at udtrykke den samme ide) for at hjælpe eleverne med at opnå en fælles og korrekt forståelse af ulige og lige tal. Ligesom med gentagelsestrækket er formålet også her at bede eleverne forklare, hvordan de tænker. Dette kan give indsigt i deres tænkning og hjælpe dem med at engagere sig i hinandens tankeprocesser.
Samtaletræk 4: Tilføje
Underviseren forsøger at inddrage flere elever i diskussionen og spørger, om de andre elever har nogen kommentarer. I det følgende eksempel anvender underviseren først gentagelsestrækket for at tydeliggøre to påstande. Derefter anvender underviseren tilføjelsestrækket:
Underviser (U): Vi har to forskellige ideer her i klassen om tallet 6. August, du siger, at 6 er et ulige tal, fordi du kan dele det i 3 lige store dele, ikke sandt?
August: Ja.
U: Og Anne, du siger, at det er et lige tal, fordi du kan dele det i to lige store dele. Er det rigtigt?
Anne: Ja.
U: Okay, hvad med jer andre? Hvem vil tilføje noget til diskussionen? Er I enige eller uenige med August og Annes ideer? Fortæl, hvad I tænker, eller tilføj noget til andres kommentarer.
Over tid kan dette træk bidrage til, at eleverne bliver mere villige til at dele deres egne tanker og ideer i diskussioner. Det kan også være med til at etablere en norm for at se sammenhænge mellem matematiske ideer og bygge videre på dem.
Samtaletræk 5: Vente
Samtaletrækket handler om at være stille og give eleverne tid til at tænke. I det ovenstående eksempel, hvor underviseren bruger tilføje-trækket, venter læreren, og efter 45 sekunder har flere elever rakt hånden op. Ved at vente giver underviseren mulighed for, at flere elever kan deltage. Vente-trækket kan således bringe vigtige bidrag fra flere elever ind i diskussionen og signalerer samtidig en forventning om, at alle elever har vigtige idéer, de kan bidrage med.
Samtaletræk 6: Drej og snak
Samtaletrækket indebærer, at underviseren beder eleverne om at dreje sig eller vende sig mod deres sidekammerat for at diskutere et spørgsmål eller en påstand. Eleverne får mulighed for at tydeliggøre deres ideer ved at dele dem med hinanden og bliver dermed orienteret mod hinandens tænkemåder. Mens eleverne diskuterer, går underviseren rundt og lytter til deres samtaler. Derved opnår underviseren indsigt i, hvad eleverne forstår, og hvordan de tænker. Denne indsigt kan underviseren bruge til at udvælge de elever, som hun skal henvende sig til i klassens samtale.
Samtaletræk 7: Ændre
Samtaletrækket giver eleverne mulighed for at ændre deres måde at tænke på undervejs. Eleverne får chancen for at revurdere og justere deres tænkemåde baseret på nye input i undervisningen. At ændre svar eller påstand undervejs, efter at have fået ny indsigt, bliver dermed en naturlig del af elevernes læringsproces.
Disse samtaletræk kan skabe et interaktivt og dynamisk læringsmiljø, hvor elevernes matematiske tanker og forståelse udvikles gennem dialog og refleksion. Ikke alle træk vil være til stede i alle samtaler – kun nogle af trækkene. Dette er tænkt som inspiration til at berige samtalerne, så de i højere grad kan styrke elevernes udvikling af matematisk opmærksomhed.
til: DAGTILBUD
emne: MATEMATISK OPMÆRKSOMHED OG DIALOGISKE INTERAKTIONER
UDGIVET: 2024
Forfatter
Birgitte Henriksen
Ph.d-studerende
DPU, Aarhus Universitet/Københavns Professionshøjskole
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Til overvejelse
- Hvilke af modellens ”samtaletræk” bruger du i undervisning i matematisk opmærksomhed?
- I hvilken udstrækning kan du anvende modellen ”samtaletræk” til at inspirere dialogisk samspil i undervisning i matematisk opmærksomhed?
Kilder
- Wæge, K. (2015). Samtaletrekk – et redskap i matematiske diskusjoner. Tangenten (2) 2015.