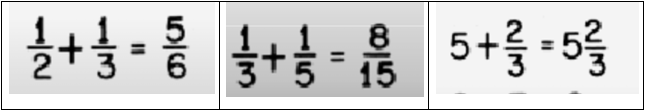Spændende udkast til opgaver med brøker til forskellige EUD-uddannelser
Nedenfor er ni udkast til opgaver, som kunne være inspirerende og lærerige for elever på forskellige typer erhvervsuddannelser. Vi skriver ”udkast”, da de er lavet som inspirationsmateriale, hvor lærerne kan tage idéen og herudfra justere i fx teksten og lave sit eget materiale udformet på en facon, som passer bedst til en bestemt elevgruppe.
Eksempel 1: Ændring af løn for en deltidsansat
Eksemplet er fra virkeligheden, dog er navnene på kirkerne og lønsatsen ændret for anonymisering. Erhvervsfagligt ligger casen inden for handels- og kontorområdet. Casen er, at Stefanuskirken har en kordegn ansat, som ikke er på fuld tid. I løbet af budgetåret får kordegnen nye opgaver, og lønnen skal derfor tilrettes i det løbende budget. Da en arbejdsuge i Danmark er på 37 timer, giver dette anledning til nogle pragtfuldt ”skæve brøker” – 37.-dele. For at lede eleverne gennem sådanne udregninger foreslår vi en specifik rækkefølge i opgaven/beregningen, så eleven også løbende forstår, hvad der sker.
Intro til opgaven - Overordnet om kordegnens løn:
I overenskomsten for kordegne er der forskellige trin, løngrupper (LG), som man indplaceres på, alt efter hvilke funktioner man har i den konkrete kirke. Disse løngrupper er ikke et fast beløb men et interval (derfor ordet ”top”), hvor man igen kan indplacere en kordegn alt efter dennes tidligere erfaring mm.
I Stefanuskirken har man en overenskomstansat kordegn (LG2, top), hvor den årlige grundløn (pr. 1/4-2022) for fuld tid er kr. 393.903,00. I tillæg får kordegnen et rådighedstillæg på kr. 35.270,63 og et OK18-tillæg på kr. 850,58.
- Udregn hvad den årlige løn er, inkl. tillæg, hvis kordegnen er på fuld tid: ______
(Svar: Addition af de tre beløb: $393.903,00 + 35.270,63 + 850,58 = 403.024,21$)
- I tillæg får kordegnen pension, som udgør 18% af den årlige løn, og et årlige ferietillæg på 1,5%. Udregn den årlige løn, inkl. pension og årligt ferietillæg, hvis kordegnen er på fuld tid: ______
(Svar: Udregnes f.eks. som: $403.024,21 \cdot 1,18 \cdot 1,015 = 515.040,00$)
- Kordegnen er dog ikke ansat på fuld tid, men 28 timer per uge. Udregn kordegnens årlige løn, der svarer til 28 timer per uge: ______
(Svar: Udregnes f.eks. som: $515.040,00 \cdot \frac{28}{37} = 389.760,00$ kr.)
- Stefanuskirken har en nabokirke, Christianskirken, som låner Stefanuskirkens kordegn 3 timer per uge til personregistrering. Udregn det årlige beløb, Christianskirken skal betale til Stefanuskirken for lån af kordegnen: ______
(Svar: Udregnes f.eks. som: $389.760,00 \cdot \frac{3}{28} = 41.760,00$ kr.)
- Kordegnen får midt på året mulighed for at gå op i tid til 32 timer per uge per 1. august. Udregn kordegnens samlede løn for resten af året: _____
(Svar: Udregnes f.eks. som: $515.040,00 \cdot \frac{5}{12} \cdot \frac{32}{37} = 185.600,00$ kr.)
Når man laver sådanne opgaver, er det relevant at inddrage en diskussion af antal betydende cifre, og hvad der er tradition for i et budget forskellige steder. Skriver man fx det præcist udregnede tal med to betydende cifre, eller rundes der af i et budget i den konkrete virkelighed?
Eksempel 2: Brøker til at blive klogere på sportens verden
Mange elever er interesserede i sport og er måske tæt på eksperter inden for en sportsgren. Når man ser TV med sport, kommer der nogle gange nogle statistikker frem fra kampen, f.eks. som efter 1. sæt af Holger Runes kamp mod østrigeren Dominic Thiem i Paris Masters turneringen i 2023. Man ser her, at der indgår en masse brøker i beskrivelsen af, hvordan sættet er forløbet. Ikke alle elever vil være interesserede i tennis, men de kan være interesserede i andre sportsgrene, hvor der er tilsvarende statistikker, som man kan drøfte med eleverne – få dem til at drøfte med hinanden.
I det konkrete eksempel fra tennis ser vi, at Holger Rune vandt første sæt 6-4. Man kan her diskutere, på hvilke områder Rune var bedre end Thiem. TV2 har angivet med gult, hvem der har præsteret bedst, men ikke hvor meget bedre. For eksempel har Thiem vundet flest point fra baglinjen, 15 ud af 33, mod Runes 12 ud af 27, men hvis man ser på procenterne, er tallene henholdsvis 45% (0,45) og 44% (0,44). Brøkerne i bunden er rent faktisk meget tæt på hinanden. Vi ser dog også, at ift. hvem der har vundet flest net points, så står de lige, da 4 point ud af 6 er det samme som 8 ud af 12.
Hvor er så den største forskel? Rune har flest vindere, 16 ud af i alt 25 – dvs. 64% (0,64), hvorimod Thiem har færrest uprovokerede fejl (altså fejl, der alene skyldes, at man selv har spillet dårligt, ikke at man er blevet presset til at lave en fejl – en såkaldt provokeret fejl), 10 ud af i alt 24 – dvs. 42% (0,42). I deres kamp var det tilsyneladende bedre at lave vindere end at undgå at lave fejl – det vandt Rune (bl.a.) på. Et kuriosum her kunne være, at hvis man ser nærmere på brøkerne for netpoints, som jo matematisk set var ens, da $\frac{4}{6}=\frac{8}{12}$, så kunne man evt. konkludere, at Runes modighed belønnes. Rune har prøvet dobbelt så mange gange som Thiem og rent faktisk fået flere points her, så selvom deres succesrate var ens, kan det i selve kampen være blevet belønnet at prøve at være offensiv frem for defensiv. Det vil sige, nogle gange er 4/6 og 8/12 ikke helt ens. Sådanne data kan bruges til at motivere elever til at lære om brøker og om brøkers betydning.
Eksempel 3: Brøker i demokratiets verden
ET TÆNKT EKSEMPEL FRA KOMMUNALVALG
Eksemplet her viser, hvordan forholdstalsvalg opgøres, og mandater fordeles i kommunalvalg i Danmark efter den såkaldte d’Hondske metode. Den er opkaldt efter en belgisk jurist ved navn Victor D’Hondt (1841-1901). Overordnet fordeles mandaterne først på listeforbund og kandidatlister. Derefter fordeles de vundne mandater inden for listerne. Fordelingen af mandater sker ved, at stemmetallene fra valget divideres med henholdsvis 1, 2, 3, 4 osv. Det vil sige, at man finder brøktallene for det hele (1/1), det halve (½), en tredjedel (1/3), en fjerdedel (1/4) osv.
Det største af alle disse nye brøktal afgør, hvem der vinder det første mandat. Det andetstørste brøktal afgør det andet mandat. Det tredjestørste brøktal afgør det tredje mandat. Og så fremdeles.
Man kan i den forbindelse diskutere, om metoden favoriserer henholdsvis større eller mindre partier.
For at sikre at eleverne finder en opgave om valg relevant, vil vi opfordre til, at man fx bruger lokale tal; det kunne være valg til TR-repræsentant, elevråd, egen kommune eller andet. Nedenfor har vi konstrueret et eksempel ud fra en tænkt situation, hvor 4000 borgere har stemt til kommunalvalg i en kommune, og vi viser nogle muligheder ved et tænkt eksempel med 4000 borgere.
Forestil jer, at stemmetallene ser sådan ud:
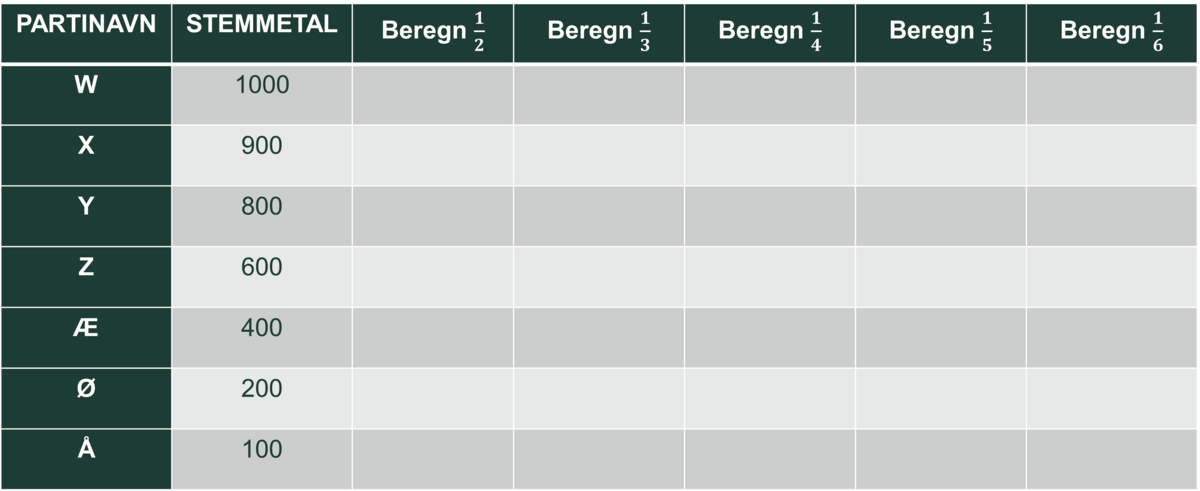
Spørgsmål 1: Er det korrekt, at 4000 borgere har stemt? Har I brugt nogle smarte metoder til at kontrollere, om der var 4000 stemmer?
Til alle danske kommunalvalg beregner man brøktallene for at finde ud af, hvem der skal i kommunalbestyrelsen.
Spørgsmål 2: Tænk over, hvilke brøktal som I lettest kan beregne i hovedet. Regn dem ud i hovedet, og skriv dem ind i dette skema med en blå farve. Snak også om, hvilke smarte metoder I brugte.
Spørgsmål 3: Beregn resten af brøktallene, og skriv også dem med rødt i skemaet:
Spørgsmål 4:
Tænk over, hvordan tallene i tabellen kan stilles op i rækkefølge efter størrelse. I kan skrive det ind her:
Spørgsmål 5:
Hvilke partier er i kommunalbestyrelsen:
Hvis der er 8 medlemmer?
Hvis der er 16 medlemmer?
Hvis der er 24 medlemmer?
Besvarelser
Besvarelse af spørgsmål 2:
Besvarelse af spørgsmål 3:
Besvarelse af spørgsmål 4:
Besvarelse af spørgsmål 5:
Find ud af, hvilke partier der er i kommunalbestyrelsen.
Hvis der er 8 medlemmer:
Hvis der er 16 medlemmer:
Hvis der er 24 medlemmer:
Eksempel 4: Bilsalg
I december 2021 var ¼ af alle bilsalg elbiler. Hvad kunne det fx være af antal – og hvordan ser det ud nu?
For hver hybridbil blev der solgt tre dieselbiler. Hvad kunne det fx være af antal – og hvordan ser det ud nu?
Om eksempel 5-8
De følgende eksempler 5 – 8 viser, at der kan knytte sig mange forskellige sproglige udtryk til brøker inden for forskellige erhvervsfaglige områder. Det er vigtigt at have særligt fokus på de sproglige udtryk, der anvendes i de erhvervs- og EVU-kurser, som eleverne stiler imod. I de følgende opgaver kan I samtale netop med fokus på sproget, og der indgår ikke specifikke tal og beregninger.
Eksempel 5: Metal
Disse ord med relation til brøker bliver af og til brugt i metalfaget. Hvilke af dem har I mødt?
Målforhold
Forholdstal
Procent
Decimalregning
Ægte brøk
Blandede tal
Eksempel 6: Handel & konto
Disse ord med relation til brøker bliver af og til brugt i handel & kontor. Hvilke af dem har I mødt?
Promille
Priskurant
Akkordløn
Bruttoavance
Den samlede indkøbsoplevelse / den forventede indkøbsoplevelse skal gerne være højere end 1.
Indekstal
Fx en butik kalkulerer fast faktor 2,75. Beregn salgspris når kostpris på kjole eksklusive moms er 440 kr.
Fx beregn indekstal for 3 måneder i år og sidste år. Er det gunstigt?
Eksempel 7: Bygge og anlæg
Disse ord med relation til brøker bliver af og til brugt i bygge og anlæg. Hvilke af dem har I mødt?
Akkordløn
Skitse i 1:20
Tegn i målforhold og mål på tegning
Eksempel 8: Metoder til procentberegning, som voksne anvender
Blandt 160 AMU-kursister i et studie af Lindenskov (1996) fandtes der 8 forskellige metoder til løsning af:
’En skjorte er nedsat med 30% fra 249,75 kr. Hvor meget skal du betale?’
I kan i undervisningen bede eleverne om at se, om de kan finde på mange metoder, fx på otte metoder?
Eksempel 9: Brøker i verdensrummet
Dette eksempel omhandler, at Voyager 1 blev sendt afsted fra Cape Canaveral i 1977 ud i rummet. Ombord er bl.a. en forgyldt kobberskive som en tidskapsel om livet og kulturen på jorden, og på disken er der skrevet tre brøkudtryk:
Få evt. elever til at overveje, hvorfor man sendte brøkudtryk ud i verdensrummet, og hvorfor netop disse tre.
Kilder
- Lindenskov, L. (1996). “Det er fordi jeg mangler billeder…” AMU-kursisters oplevelser og potentialer i faglig regning og matematik. København: Arbejdsmarkedsstyrelsen.
- NASA: Voyager - The Golden Record (nasa.gov) Voyager - The Golden Record (nasa.gov)
til: ERHVERVSSKOLE
emne: BRØKER PÅ ERHVERVSSKOLER
UDGIVET: 2024