Fire situationer, der kan repræsenteres med brøker
Brøker anvendes til forskellige ting – noget som også kan virke forvirrende på elever:
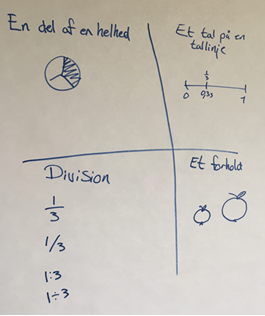
- Brøker som angivelse af en del af en helhed
- Brøker som et tal – et rationalt tal, der kan repræsenteres som et punkt på en tallinje
- En division og dens resultat
- En måde at sammenligne størrelsen af to mængder på – et forhold
Figuren til højre illustrerer de fire ovennævnte situationer.
Nederst i højre hjørne åp figur 2 illustreres forhold med æbler. Man kan også benytte en ligebenet trekant i stedet for æblerne for at illustrere forhold. Nogle elever vil bedst forstå det med æblerne, andre med trekanterne, og vi anbefaler at vise både matematikeksempel som fx trekanterne og hverdagseksempel som fx æblerne.
Forskellige repræsentationer, der betyder det samme, er svært, men kan være lærerige og brugbare
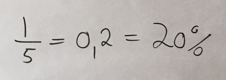
Når brøker kommer ind i billedet, ændrer det radikalt elevernes syn på tal. Rent læringspsykologisk må der ske en stor forandring af elevernes talbegreb, og det kalder den schweiziske psykolog Jean Piaget (1896 – 1980) akkomodation. Forandringen er radikal i og med, at der nu skal to tal til at angive ét tal! Og som om det ikke skulle være nok, så bruges der mange forskellige symboler til at skrive disse tal. Til højre ses et eksempel på tre forskellige symboler til at skrive det samme tal, nemlig som brøk med tæller og nævner, som decimalbrøk og som procent.
I tillæg til de illustrationer, som blev gengivet på posteren, kan man også anvende $\frac{20}{100}$ og $\frac{2}{10}$ osv.
Ud over at man ved brøker bruger to tal til at angive et enkelt tal, så gør brøker det også muligt, at samme tal kan skrives på mange forskellige måder som tæller og nævner, og elever kan blive i tvivl om, om det faktisk er det samme tal. For eksempel er $\frac{1}{6}$ helt det samme tal som $\frac{2}{12}$ og $\frac{3}{18}$ og i øvrigt også alle mulige andre brøker, der kan skrives som $\frac{a}{6a}$, hvor nævneren er seks gange så stor som tælleren.
Som en yderligere kompleksitet i symbolbrugen ved brøker kan stregen mellem tæller og nævner både tegnes som vandret brøkstreg og på skrå med /. Den sidste gør det muligt at skrive en brøk på en linje digitalt, men den er ikke praktisk, hvis tæller eller nævner har flere led. Når den skrå linje anvendes, skal der tillige anvendes parenteser rundt om tæller og nævner for at sikre, at udtrykket repræsenterer den rigtige brøk.
I matematik i dag foretrækker man den vandrette brøkstreg. Det er praktisk, fordi man så kan repræsentere brøker, hvor tæller eller nævner består af flere led. Brøkstregen tegnes blot så lang, som der er brug for. Man kan dog også i anden litteratur se brøker betegnet med skrå brøkstreg; muligvis af layout-hensyn. Dog skal den skrå brøkstreg ikke forstås som en divisionsstreg/divisionstegn. Det er det ikke – selvom man kan læse på mange hjemmesider, at en brøk bare er en division.
I parentes bemærket: Når det drejer sig om symbolet for division, ændrer det sig også gennem tiden og i forskellige kulturer. I engelsktalende lande bruger man ofte et minustegn med en prik over og en prik under som symbol på division (også illustreret i Figur 2). I ældre tid i Danmark var det symbolet for subtraktion.
Vi anbefaler, at man fx lægger mærke til, hvilken opskrivning ens elever bruger – og se det som fordel for holdet, hvis dine elever har forskellige opskrivningsmetoder, fx hos flygtninge med undervisningserfaring fra andre skolesystemer.
Forskellige symboler for brøker historisk og deres brug i dagligsproget
I Egypten i oldtiden accepterede man kun stambrøker (enhedsbrøker) med 1 som tæller og så også to tredjedele. Stambrøkerne blev dengang skrevet som en mund øverst og nævneren nedenunder.

Derudover er der også det mundtlige, naturlige sprog / dagligsproget – hvilke udtryk bruger vi, når vi taler om brøker eller læser noget med brøker højt? For eksempel hedder ¼ en fjerdedel eller en kvart på dansk, mens ½ ikke hedder en toendedel, men blot en halv.
Når vi bruger brøker til at beskrive familierelationer, bruger vi kun det naturlige sprog – ikke symboler eller billeder. For eksempel bruger man udtrykket ”halvsøster/halvbror” til at beskrive, at man har netop én fælles forælder, og udtrykket ”halvkusine/halvfætter” til at beskrive en person, om hvem vores forældre er fætter/kusine (ogle kalder også dette for grandfætter/grandkusine, men den rigtige betydning af grandfætter/grandkusine er, at disse er ens forældres fætre/kusiner). Halvkusine/halvfætter kan også være en relation til en halvsøskende; og tilsvarende med ”kvartkusine/kvartfætter”, hvor ens forældre er halvfætre/halvkusiner. Pudsigt nok bruges ordenstallene på engelsk til at beskrive disse familierelationer som henholdsvis ”second cousin” og ”third cousin". Det er også sproglige konventioner, som må læres i tillæg til det begrebslige indhold i brøker.
Forskellige repræsentationer kan bruges til at afgøre, hvor store brøker er i forhold til andre brøker
Fra forskningen ved man, at mennesker bruger forskellige metoder og repræsentationer til at sammenligne størrelsen af forskellige brøker. Clarke og Roche (2009) fandt, at elever bruger en række forskellige repræsentationer og tankegange:
- Nogle oversætter brøksymboler eller den mundtligt udtalte brøk til en fysisk repræsentation.
- Nogle oversætter brøksymboler eller den mundtligt udtalte brøk til en tegnet illustration, fx hvor en enhed er tegnet som en rektangulær blok eller som en cirkelformet pizza.
- Nogle ser kun på tællerne og sammenligner deres størrelser – denne metode giver korrekt svar, hvis og kun hvis nævnerne er ens.
- Nogle ser kun på nævnerne og sammenligner deres størrelser – denne metode giver korrekt svar, hvis og kun hvis
- tællerne er ens
- og elevens ved, at store nævnere giver mindre brøker end små nævnere.
- Nogle sammenligner med et kendemærke, fx større eller mindre end ½.
- Nogle genfortolker brøkerne, så de får samme nævner (i skolematematik kaldes det ofte 'omskriver til fællesnævner'), hvorefter tællernes størrelse sammenlignes.
- Nogle ser på absolut forskel mellem tæller og nævner (nævner – tæller), og konkluderer fx at $\frac{5}{6}$ har samme størrelse som $\frac{7}{8}$, fordi tælleren er 1 mindre end nævneren i begge brøker.
Derfor anbefaler Prediger m.fl. (2022), at man som lærer lægger sig på sinde, at der ikke er én bestemt rækkefølge (targeted steering trajectories), som er den ’rigtige’ at følge i sin undervisning, og som passer til alle elever. Man må som lærer prøve at få indblik (ved at lytte, iagttage og samtale) i elevernes opfattelser og metoder og tilpasse sin undervisning, så elevernes opfattelser og metoder på en effektiv måde kan ledes frem til undervisningens mål. Bruger dine elever fx nogle af repræsentationerne og metoderne a) til g), så kan I på holdet tage udgangspunkt i det.
Fra Martin m.fl. (2012) ved man, at illustrationer på papir eller skærm er gode som støtte for elevers forståelse af brøker, og at fysiske repræsentationer er endnu bedre end illustrationer på papir eller skærm til at styrke forståelsen af brøker. Vores anbefaling er derfor, at I som lærere kombinerer symbolske repræsentationer både med illustrationer og fysiske repræsentationer for at styrke forståelsen af brøker, modellering med brøker og regning med brøker. De fysiske repræsentationer kan eventuelt være taget fra den konkrete erhvervsuddannelse, som ens elever uddanner sig til.
Dette hænger også sammen med, at man ifølge Duval (2006) bruger fire typer repræsentationer, som kaldes semiotiske registre:
- det skriftlige naturlige sprog
- det mundtlige naturlige sprog
- det symbolske register
- det billedlige register
Duval mener, at for virkeligt at mestre et matematisk begreb må man kunne oversætte mellem disse registre, dvs. at man kan springe fra den ene form for repræsentation til den anden. I den forbindelse kan elektroniske værktøjer som fx en lommeregner også bruges til at udregne brøker.
Brugen af enheder
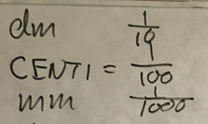
For erhvervsuddannelserne er der et yderligere element, der er vigtigt, nemlig at stambrøkerne (dem hvor tælleren er 1) også angiver størrelsen af en enhed. Fx SI-enheder hos elektrikere. Hvis vi taler om længdeenheden 1 meter, så betyder $\frac{1}{10}$, at der er tale om decimeter (dm), mens $\frac{1}{100}$ gør, at vi taler om centimeter (cm) osv. Dette er yderligere en komplikation.
Forholdsregning

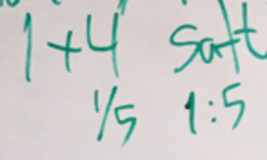
Mange – ikke kun elever – oplever forvirring omkring, hvordan man beskriver forhold, for eksempel når man køber en flaske koncentreret saft, og der står, at der skal fortyndes 1:5 for, at den er drikkeklar. Hvad betyder det? Skal 1:5 forstås som division, altså at der skal være 1/5 saft og derfor 4/5 vand? Dette er ikke korrekt. Kolonet i 1:5 skal her læses som 1 del saft og 5 dele vand. Dvs. der er rent faktisk 1/6 saft i den færdige blanding.
For at undgå misforståelser skriver nogle producenter somme tider 1+5 som i Figur 6. Set fra et rent matematisk synspunkt er det ukonventionelt at beskrive et forhold som 1+5, men måske er 1+5 enklere at forstå intuitivt. Den angiver, at 1 del saft (f.eks. en kop) skal blandes (”plusses”) med fem kopper vand. Men dette angiver jo netop, at den færdige blanding består af 6 kopper væske, hvoraf en kop er saft; dvs. 1/6.
I forhold til saft er det i praksis ikke så farligt, hvis man blander forkert, og smag og behag er i øvrigt forskellig. Er saften enten for tynd eller for stærk, hælder man enten mere saft eller mere vand i beholderen. Det er straks meget mere alvorligt, hvis det handler om en cementblanding eller en medicinopløsning. Her må der ikke regnes forkert.
Rent faktisk er det så vanskeligt, at man indimellem finder forkerte beregninger i officielle dokumenter med instruktioner om at lave opløsninger. Se eksempel nedenunder.
Her opfattes 1:10 (forkert) som 1/10.
Måske på grund af vanskeligheden med at forstå blandingsforhold ser man nogle gange, at det simpelthen siges med ord. Et eksempel ses på tv2.dk den 7. januar 2024 (https://nyheder.tv2.dk/samfund/2024-01-07-vintervejret-er-saa-voldsomt-at-kommune-bruger-grus-i-stedet-for-salt), som rapporterer, at der på grund af den hårde frost ikke længere blev strøet salt i Aarhus Kommune, da saltet er virkningsløst ved disse temperaturer. I stedet strør man en blanding af salt og sand. I teksten på TV2 står der: ”Blandingsforholdet hedder tre sand til en salt". Skal dette skrives med kolon, vil der være salt til sand i blandingsforhold 1:3. Dvs. ¼ salt og ¾ sand.
Også i brugsanvisning til kemiske produkter i husholdningen bruger producenter nu om dage almindeligt hverdagssprog, som fx 1 del eddikesyre til 2 dele vand i Figur 8.

Brøker med bogstaver
Nogle gange ser man brøker med bogstaver. Det ser man fx i formler, og så kan man tænke længe over, hvilken indflydelse det har, hvis bogstaverne i nævneren kan erstattes med meget store eller meget små tal. Og det samme med tællerens bogstaver.
Kilder
-
Christiansen, T., Bagh, T., & Andersen, K. (2024). Egypten i oldtiden – videnskab. Den Store Danske på lex.dk. Hentet 4. januar 2024 fra https://denstoredanske.lex.dk/Egypten_i_oldtiden_-_videnskab.
-
Clarke, D., & Roche, A. (2009). Students’ fraction comparison strategies as a window into robust understanding and possible pointers for instruction. Educational Studies in Mathematics 72(1), 127–138.
-
Duval, R. A. (2006). Cognitive Analysis of Problems of Comprehension in a Learning of Mathematics. Educ Stud Math 61, 103–131.
-
Martin T., Svihla, V., & Smith, C. P. (2012). The role of physical action in fraction learning. Journal of education and human development 5(1), 1–17.
-
Prediger, S., Quabeck, K., & Erath, K. (2022). Conceptualizing micro-adaptive teaching practices in content-specific ways: Case study on fractions. Journal on Mathematics Education 13(1), 1–30.
til: ERHVERVSSKOLE
emne: BRØKER PÅ ERHVERVSSKOLER
UDGIVET: 2024
