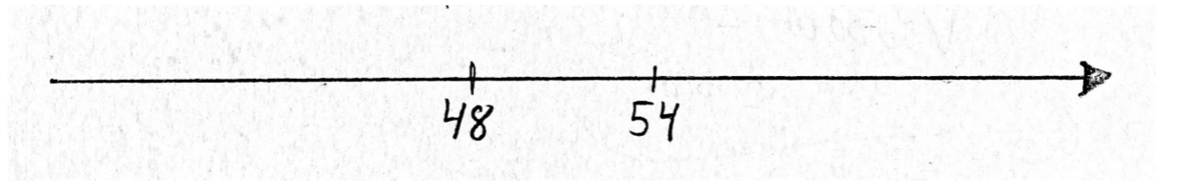Addition og subtraktion - Hvordan?
En række forskningsresultater underbygger argumenter for, at undervisning i beregninger med flercifrede tal bør sigte på, at eleverne kommer til at kunne bruge regnestrategier fleksibelt og/eller på, at elever selv deltager i udviklingen af metoder til at regne med flercifrede tal (se også Hvad siger forskningen?). Sådanne tilgange til undervisning i beregninger står i modsætning til undervisning, hvor eleverne får vist en algoritme, som de efterfølgende træner.
Mange matematiklærere føler sig imidlertid ikke så godt hjulpet til at undervise i fleksibelt brug af regnestrategier og i udvikling af metoder til beregninger. Hvordan kan en sådan form for undervisning se ud, og hvilken progression kan den følge? Denne tekst beskriver de grundlæggende træk i en række forskeres bud på undervisning i flercifret addition og subtraktion (kilde 1, 2 og 3).
-
En regnestrategi er den måde, man håndterer de tal, der indgår i en beregning, med henblik på at finde frem til et resultat (kilde 1).
-
At en person kan bruge regnestrategier fleksibelt vil sige, at personen råder over forskellige mulige strategier til beregninger og kan vælge en strategi, der er hensigtsmæssig for hende/ham i en bestemt beregning (kilde 1).
-
En metode til at regne med flercifrede heltal opfattes i denne sammenhæng som en på forhånd fastlagt strategi og skrivemåde, der kan bruges generelt i forbindelse med en regningsart.
Problemer fra elevernes hverdag
Undervisning i flercifret addition og subtraktion kan begynde, når eleverne både har viden om flercifrede tal og erfaringer med etcifret addition og subtraktion. Undervisningen bygger i høj grad videre på disse erfaringer.
Problemer fra elevernes hverdag er et godt udgangspunkt (kilde 2). Udgangspunktet er altså ikke regneudtryk med talsymboler, men hverdagsproblemer, som læreren formidler mundtligt til klassen, og som eleverne kan leve sig ind i. På den måde kommer undervisningen til at belyse, hvad det er for typer af problemer, addition og subtraktion kan bidrage til at løse. Samtidig kan selve problemer give ideer til, hvordan man kan tænke for at løse dem.
I forbindelse med addition drejer en typisk problem sig om at ’lægge til’, og i forbindelse med subtraktion drejer et typisk problem sig om at ’trække fra’. Der er imidlertid flere typer problemer, der er forbundet med addition og subtraktion - se evt. oversigten over de såkaldte additive situationer i temaet ’At regne med etcifrede tal’.
Eksempel, sammenligning, addition:
- Ole har 54 kroner. Heidi har 48 kroner mere end Ole. Hvor mange penge har Heidi?
Eksempel, sammenligning, subtraktion:
- Ole har 54 kroner, og Heidi har 48 kroner. Hvor mange penge har Ole mere end Heidi?
TIL OVERVEJELSE I FAGTEAMET
- Har I ideer til problemstillinger fra hverdagen, der involverer addition med flercifrede tal, og som elever i 2. klasse vil kunne ’se for sig’? Se evt. oversigten i teksten ’Additive og multiplikative situationer’ fra temaet ’At regne med etcifrede tal
En model af problemet
For at løse et beregningsproblem kan eleverne støtte sig op ad konkrete materialer eller tegninger. Det kan fx dreje sig om klodser, der repræsenterer 1´ere og 10´ere eller om åbne tallinjer. I første omgang kan eleverne bruge materialet eller tegningen til at lave en model af problemet. Derefter kan de bruge materialet eller tegningen til at finde resultatet ud fra den viden og kunnen, de har i forvejen. Det er typisk, at eleverne i begyndelsen bruger materialet på en måde, som ligger tæt op ad det problem, de løser.
Eksempler
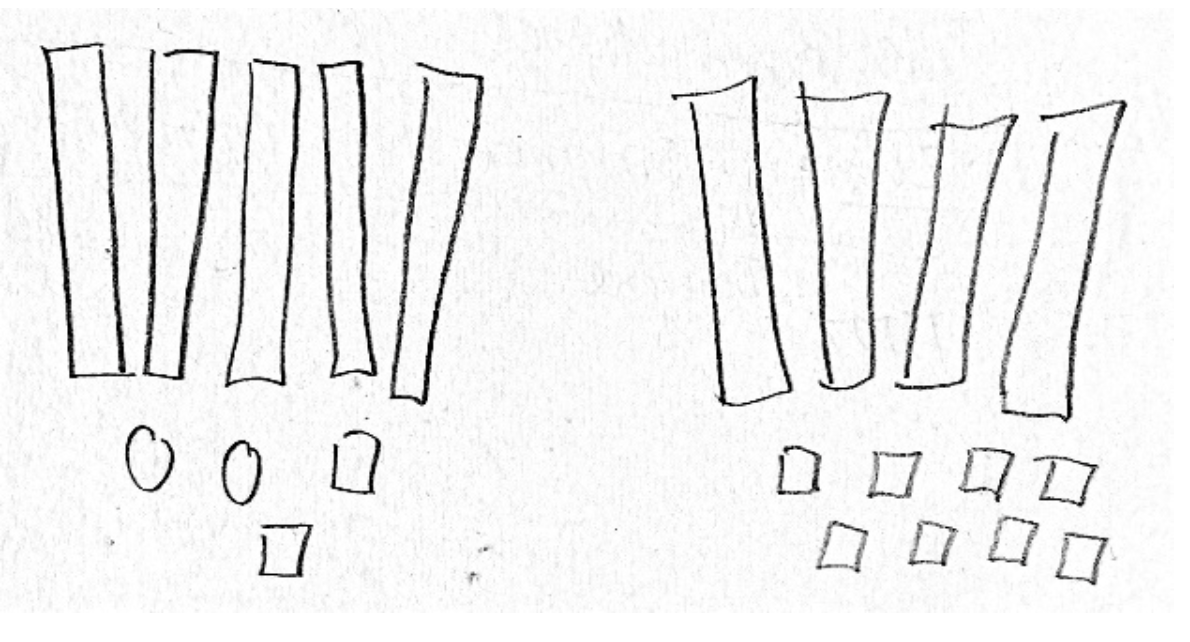
Materialet herunder kan fx bruges til at lave modeller af begge problemer fra eksemplet i forrige afsnit.
- Ole har 54 kroner. Heidi har 48 kroner mere end Ole. Hvor mange penge har Heidi?
En elev kan fx forestille sig, at der kommer 48 kroner ’oven i’ de 54 kroner. Måske udnytter hun materialet og sin viden om 10´ere og tæller ’fire tiere op’: 64, 74, 84, 94. Derefter tæller hun 1´ere: 95, 96, … 102.
- Ole har 54 kroner, og Heidi har 48 kroner. Hvor mange penge har Ole mere end Heidi?
En elev kan fx tænke: Ole har en 10´er mere end Heidi, men Heidi har 4 enere mere end Ole.
Hvis jeg lægger 10 til Heidis bunke og trækker 4 fra, har de lige mange, altså $54 - 48 = 10 - 4 = 6$.
En tegningen af en åben tallinje kan også bruges til at lave modeller af begge problemer fra eksemplet i forrige afsnit.
- Ole har 54 kroner. Heidi har 48 kroner mere end Ole. Hvor mange penge har Heidi?
En elev kan fx tænke: ’Jeg står på 54 og skal 48 op. Først hopper jeg 40, så jeg kommer op på 94. Jeg mangler at hoppe 8. Der er 6 op til 100. Jeg mangler stadig at hoppe 2 mere. Det bliver 102.
- Ole har 54 kroner, og Heidi har 48 kroner. Hvor mange penge har Ole mere end Heidi?

En elev kan fx finde forskellen mellem 48 og 54 ved at tænke, hvor langt er der fra 48 og op til 54 på tallinjen? Måske siger hun: ’Op til 50 er der 2. Fra 50 til 54 er der 4. Det bliver 6 i alt’.
Fleksible strategier
Eleven i det forrige eksempel med 54 - 48 bruger en bestemt strategi til at løse opgaven. Strategien omtales som en sekventiel strategi eller som en hoppestrategi (jump-strategi). I denne strategi opfattes tallene som objekter på en tallinje, og beregninger opfattes som bevægelser frem og/eller tilbage langs tallinjen (kilde 1 og 3). Ud over den sekventielle strategi omtales i forskningen også opdelingsstrategier og varierende strategier (også kaldet kompensationsstrategier) (kilde 1, 3 og 4).
Opdelingsstrategier går ud på at tænke tallene som opdelte, fx i 1´ere, 10´ere, 100´er osv.
Eksempel (54 + 48):
Jeg deler 54 op i 50 og 4. Så deler jeg 48 op i 40 og 8. Når jeg lægger tierne sammen, får jeg 90. Når jeg lægger enerne sammen, får jeg 12. Så bliver det hele til 102.
Eksempel (54 - 48):
Jeg deler 54 op i 50 og 4. Jeg skal tage 48 væk. Jeg tager først 40 og 4 væk. Nu er der 10 tilbage, og jeg mangler at tage 4 væk. Resultatet bliver 6.
Varierende strategier går ud på at ændre på tallene, så de bliver lettere at regne med. Derefter kompenserer man for ændringen.
Eksempel (54 + 48):
Jeg tænker først 54 plus 50. Det er 104. Men jeg skulle ikke lægge 50 til, kun 48. Derfor tænker jeg 104 minus 2. Det er 102.
Eksempel (54 - 48):
Jeg lægger 2 til begge tal, da det giver samme forskel. Så kan jeg tænke 56 minus 50. Fra 50 op til 56 er der 6. Så bliver 54 minus 48 også 6.
I forskningen er der bred enighed om, at det er hensigtsmæssigt at støtte elever til at bruge strategier fleksibelt (kilde 1, 2 og 3). Tanken er, at eleverne skal komme til at råde over flere forskellige strategier og gradvist blive i stand til at vælge en strategi, der er hensigtsmæssig til netop den beregning, de skal foretage. Samtidig er elevernes tænkning direkte forbundet med deres forståelse.Det er værd at være opmærksom på, at strategier til subtraktion kan have forskellige udgangspunkter. I subtraktionen 54 - 48 kan eleverne fx tage udgangspunkt i 54 og tænke, at 48 skal tages væk (fx ved at ’hoppe baglæns’ på en tallinje) eller, ’hvor meget skal jeg tage væk fra 54 for at komme ned på 48?’ Eleverne kan også tage udgangspunkt i 48 og tænke, ’hvor meget skal jeg lægge til for at komme op på 54?’ Det sidstnævnte udgangspunkt omtales som indirekte addition. Forskning tyder på, at mange elever har lettest ved flercifret subtraktion, når de tænker det som indirekte addition (kilde 3 og 4).
Elevernes udvikling af fleksibelt brug af strategier kan bl.a. støttes ved at
- vælge problemstillinger, der lægger op til forskellige typer af tænkning
- vælge repræsentationer, der støtter forskellige typer af tænkning
- eleverne forklarer og sammenligner deres forskellige strategier
- eleverne diskuterer, hvilken strategi der er smartest i forskellige beregninger
- læreren kommer med forslag til strategier, som eleverne skal følge og vurdere.
TIL OVERVEJELSE I FAGTEAMET
Her er et problem:
Line sparer sammen til et spil, der koster 479 kroner.
Hun har 380 kroner.
Hvor mange penge mangler hun?
Problemet inviterer næsten til at bruge en varieret strategi. I stedet for at tænke ’fra 380 til 479’ kan eleverne først tænke ’fra 380 til 480’. Bagefter kan de kompensere for ændringen.
- Kan I komme på andre problemer, der inviterer til den varierende strategi? Til opdelingsstrategien? Til den sekventielle strategi?
- Overvej, hvilke strategier I kan understøtte ved at lade eleverne bruge hhv. base 10 materialer (1´ere, 10´ere,
100´er osv.) og åbne tallinjer.
Metoder
En (eller flere) af de strategier, som eleverne udvikler, kan udgøre en metode, det vil i denne sammenhæng sige en fremgangsmåde, der kan bruges til enhver beregning med naturlige tal inden for en regningsart.
Et første træk i retning af en sådan metode kan bestå i, at eleverne skal notere det, de tænker, når de regner. Eleverne kan evt. notere sideløbende med, at de bruger konkrete materialer, eller de kan gradvist erstatte de tegninger, de har støttet sig op ad, med tal og regneudtryk.

Eksempel:
I beregningen af 568 + 876 kan noter til en opdelingsstrategi fx komme til at se sådan ud:
- 500 + 800 = 1300
- 60 + 70 = 130
- 8 + 6 = 14
- 1300+130+14=1444
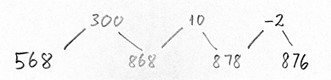
Eksempel:
I beregningen 876 - 568 kan noter til en varierende strategi fx se ud som vist herunder. Eleven har tidligere støttet sig til en tallinje, og han tænker, ’hvor langt er der fra 568 til 876?’
Et næste træk kan være, at klassen diskuterer, om der findes strategier, der kan bruges ’hver gang’, dvs. til en vilkårlig beregning inden for addition eller subtraktion med flercifrede tal. Eksemplerne herover illustrerer sådanne strategier. Strategierne nærmer sig metoder, fordi de kan bruges generelt til flercifrede beregninger. I additionen opdeles tallene i tierpotenser (1´ere, 10´ere, 100´ere osv.) som adderes for sig. Subtraktionen bygger indirekte addition, hvor tierpotenser adderes/subtraheres hver for sig. I eksemplet adderes først ’det nødvendige’ antal 100´er, derefter ’det nødvendige’ antal 10´ere, til sidst subtraheres ’det nødvendige’ antal 1´ere. Læreren kan udvælge sådanne strategier, som eleverne afprøver på forskellige beregninger, for at undersøge, om de kan ’bruges hver gang’.
Et sidste træk kan være, at læreren støtter eleverne til at bruge en overskuelig og korrekt skrivemåde. Sådanne skrivemåder kan både være lodrette eller vandrette. I lodrette skrivemåder står tallenes 1´ere, 10´ere, 100´ere … under hinanden. Nogle lærere betragter dette som en fordel, fordi det gør beregningerne mere overskuelige for elever. Andre lærere betragter det snarere som en ulempe, fordi det kan bevirke, at eleverne helt holder op med at tænke i de værdier, som cifrene repræsenterer. Risikoen er altså, at eleverne slipper deres talforståelse, når de regner. Vandrette skrivemåder samler ikke på samme måde tallenes 1´ere, 10´ere, 100´ere… Skrivemåden lægger på den måde mere op til at tænke i de værdier, som cifrene repræsenterer. Nogle fortalere for denne skrivemåde lægger også vægt på, at den vandrette skrivemåde står i tættere forbindelse med de udtryk, eleverne skal lære at håndtere senere i deres skoletid.
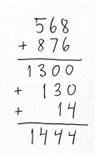
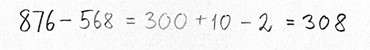
De to eksempler herover udgør metoder til hhv. addition og subtraktion. Læg mærke til, at det i additionen ikke er afgørende, om man beregner summen af 1´erne, 10´erne eller 100´erne først. Man kan altså regne fra ’venstre mod højre’. Man må dog også være opmærksom på, at nogle additioner kræver flere ’runder’ (prøv fx at beregne 378 + 424).
Metoderne er eksempler på såkaldte talbaserede metoder. Forskning tyder på, at sådanne metoder kan støtte elevers forståelse af titalssystemet, og på at elever har lettere ved at forstå og anvende talbaserede metoder frem for cifferbaserede metoder (kilde 1 og 3). Talbaserede metoder giver også ofte eleverne mulighed for en vis fleksibilitet i deres tænkning. Det er fx ikke noget brud på subtraktionsmetoden, hvis eleverne vælger at foretage beregningen ’lidt ad gangen’ (fx 100+100+100+10-2=308), i en anden rækkefølge (fx 8+0+300=308) eller i ’større skridt’ (fx 300+8=308).
I talbaserede metoder håndterer man tallene i overensstemmelse med den værdi, de repræsenterer (tallet 75 kan fx opdeles i 70 og 5). Sådanne metoder står i modsætning til cifferbaserede metoder, hvor man håndterer cifrene i tallene uden at tænke på den værdi, de repræsenterer (tallet 75 kan fx opdeles i cifrene 7 og 5).
Læg også mærke til, at metoderne ligger i direkte forlængelse af de forrige eksempler. Progressionen frem mod regnestrategier, der inkluderer en metode, er tænkt som en slags kæde:
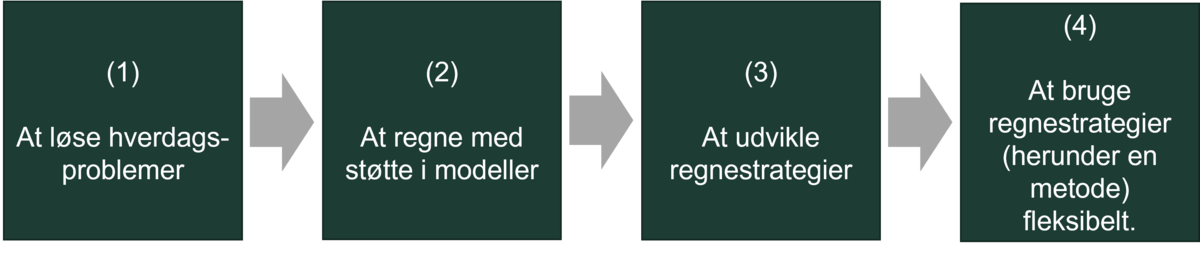
Problemerne i (1) giver baggrund for, at eleverne kan bruge modeller (2). Modellerne giver baggrund for, at eleverne, med lærerens støtte, kan udvikle forskellige regnestrategier (3). Udforskning af forskellige regnestrategier danner baggrund for, at elever kan bruge disse regnestrategier fleksibelt (4). Strategierne inkluderer en metode.
Undervejs i kæden introducerer læreren forskellige repræsentationer, som eleverne kan støtte sig op ad. I begyndelsen løser eleverne problemer fra deres hverdag ved at bruge konkrete materialer og tegninger som modeller. Senere er det hensigten, at de gradvist erstatter materialerne og tegningerne med regneudtryk - men på en sådan måde, at de konkrete materialer, tegningerne og regneudtrykkene hænger helt tæt sammen og ofte er til stede i undervisningen på samme tid. Eleverne behøver slet ikke at slippe tegningerne, skitser og noterne, hvis hensigten alene er, at de skal kunne regne fleksibelt. Hvis hensigten derimod også er, at eleverne skal blive i stand til at ’tænke i’ matematiske udtryk, er der imidlertid grund til, at undervisningen går i den retning.
Bevægelsen i kæden foregår grundlæggende ved, at klassen undersøger ’leddet’ før, og i den forbindelse bringer læreren ofte noget nyt på banen, som eleverne kan bruge til at støtte og beskrive deres tænkning. Bevægelsen fra (1) til (2) foregår fx ved, at læreren introducerer nogle konkrete materialer, tegninger og (senere) regneudtryk, som eleverne kan bruge til at støtte og beskrive deres løsning af problemer. Bevægelsen fra (2) til (3) foregår ved, at læreren introducerer nye problemstillinger og beregninger i en ren matematisk kontekst. Klassen undersøger, hvordan de konkrete materialer, tegningerne og regneudtrykkene kan bruges på forskellige måder til at addere og subtrahere.
Kæden af undervisning bygger konstant på elevernes faglige ideer, hypoteser og argumenter. De faglige pointer bygger på elevernes input, og det er elevernes input, der er afgørende for, hvornår læreren ’rykker videre’ i kæden. I den forstand deltager eleverne i udvikling af fleksibelt brug af regnestrategier, herunder i udviklingen af metoder.
Det er vigtigt at være opmærksom på, at en metode ikke udgør et slutmål i undervisningen i flercifrede beregninger. Hovedsigtet er, at eleverne udvikler forståelse for tallenes og regningsarternes egenskaber samtidig med, at de lære at regne fleksibelt. Forskning tyder på, at når elever først har lært en beregningsmetode, er der en risiko for, at de mister blik for andre strategier (kilde 3). Fx kan det i forbindelse med beregningen af 987 - 199 være mere hensigtsmæssigt at tænke ’200 mindre end 987 er 787. Resultatet er derfor 1 større, altså 788’, fremfor at bruge en bestemt metode. Med andre ord: En metode bør (kun) opfattes som en del af de fleksible strategier.
TIL OVERVEJELSE I FAGTEAMET
- Diskuter hvordan I gennem skoleforløbet vil arbejde med addition eller subtraktion af flercifrede tal. Lav en plan for arbejdet.
til: GRUNDSKOLE - Indskoling og mellemtrin
emne: ALGEBRAUDGIVET: 2022
Forfatter
Thomas Kaas
Lektor, ph.d.
Professionshøjskolen Absalon
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
-
Verschaffel, L., Greer, B. & DeCorte, E. (2007). Whole Number Concepts and Operations. I F. Lester (red.), Second handbook of research on mathematics teaching and learning (s. 557-628). Charlotte, NC: Information Age Publishing
-
Kilpatrick, J., Swafford, J. & Findell, B. (red.) (2001). Adding it up. Helping children learning mathematics. National Research Council. Washington, DC: National Academy Press.
-
Hickendorff, M., Torbeyns J. & Verschaffel L. (2019). Multi-digit Addition, Subtraction, Multiplication, and Division Strategies. I Fritz A., Haase V. G., Räsänen P. (Red.) International Handbook of Mathematical Learning Difficulties, 543-560. Switzerland: Springer. Doi: 10.1007/978-3-319-97148-3_32
-
Børne- og Undervisningsministeriet (I tryk). At subtrahere flercifrede tal. Strategisk indsats for tal- og algebraundervisning i Danmark.