Tilgang – At multiplicere flercifrede tal
Grundlæggende er der to udviklinger i læringssporet. Den ene går ud på, at eleverne gradvist udvikler fleksible måder at multiplicere på. Den anden går ud på, at eleverne gradvist udvikler deres måder at repræsentere den tænkning, de knytter til måderne. De to bevægelser foregår samtidigt over tid.
Udgangspunktet for de to bevægelser er elevernes arbejde med hverdagsproblemer, der involverer flercifret multiplikation. Disse hverdagsproblemer bør omfatte følgende fire multiplikative situationer (læs mere om multiplikative situationer i temaet 'At regne med etcifrede tal'):
- Lige store grupper
- Sammenligninger
- Rektangulære mønstre
- Kombinationer
Her er eksempler på hverdagsproblemer til hver af de fire situationer:
Lige store grupper
Fritidshjemmet skal bruge 15 liter mælk, der koster 12 kr. pr. liter. Hvor mange penge kommer mælken til at koste i alt?
Sammenligninger
Heidi har sået frø til en tomatplante. Efter 1 måned var planten 12 cm høj. Da den var udvokset, var den 15 gange så høj. Hvor høj var den?
Rektangulære mønstre
En familie vil bygge en (rektangulær) terrasse. Terrassen skal have 12 kvadratiske fliser på den ene led og 15 kvadratiske fliser på den anden led. Hvor mange fliser skal familien bruge i alt?
Kombinationer
Ole vil købe en is med to forskellige kugler is. Han kan vælge mellem 12 forskellig slags is. Hvor mange forskellige is kan han købe?
En multiplikativ situation er et problem fra elevernes hverdag, som kan løses med multiplikation og/eller division (Verschaffel, Greer og De Corte, 2007).
Fase 1
I fase 1 af læringssporet bruger eleverne konkrete repræsentationer, tegninger og evt. talsymboler til at løse problemerne med strategier, som de selv finder på. Man kan fx forestille sig, at nogle elever i forbindelse med eksemplet om rektangulære mønstre bruger centicubes eller tegninger til at visualisere terrassen og tælle sig frem til resultatet, evt. ved at skiptælle (fx 10, 20, 30, …). Man kan forestille sig, at andre elever bruger gentagen addition (15+15+15+… eller 12+12+12+12+…).
Fase 1
At løse hverdagsproblemer, der involverer flercifret multiplikation med støtte i konkrete materialer og tegninger.
Fase 2
I den følgende fase 2 fokuserer eleverne specifikt på den multiplikative situation, der vedrører rektangulære mønstre. På baggrund af et hverdagsproblem (fx problemet om terrassen) introducerer læreren en rektangel-repræsentation for multiplikation. Denne repræsentation bygger på, at multiplikation kan opfattes som en beregning, man kan foretage for at finde arealet af et rektangel. Hvis man fx vil finde arealet af et rektangel, der er 12 m på den ene led og 15 m på den anden led, kan man tænke ’12 gange tager vi 15’ (12∙15) eller ’15 gange tager vi 12’ (15∙12).
I læringssporet er det dog mindre vigtigt, at resultatet af multiplikationen svarer til arealet af rektanglet. Det vigtige er, at repræsentationen kan visualisere fx 12∙15 fliser, og at den (lidt senere i sporet) kan understøtte idéen med at opdele faktorer i fx 1´ere og 10´ere og multiplicere hver del for sig.
I fase 2 er det hensigten, at eleverne multiplicerer tocifrede tal med støtte i rektangler, der har kvadratnet som baggrund. Samtidig skal eleverne påbegynde deres udvikling af strategier til multiplikation. I løbet af fasen fokuserer undervisningen i mindre grad på hverdagsproblemer og i højere grad på multiplikation i en ren matematisk kontekst. Kvadratnettet gør det muligt, at eleverne i princippet kan tælle sig frem til resultatet af en multiplikation, men samtidig åbner det for, at de kan ’skyde genveje’ ved at anvende andre strategier end tælling. De strategier, eleverne kan bruge i tilknytning til rektangelrepræsentationen, kan kategoriseres i tre typer, som de bør få mulighed for at lære: Sekventielle strategier, opdelingsstrategier og kompensationsstrategier.
Her er eksempler på, hvordan elever kan udtrykke brug af hver af de tre typer strategier:
Fase 2
At multiplicere flercifrede tal med støtte i rektangler med kvadratnet og talsymboler.
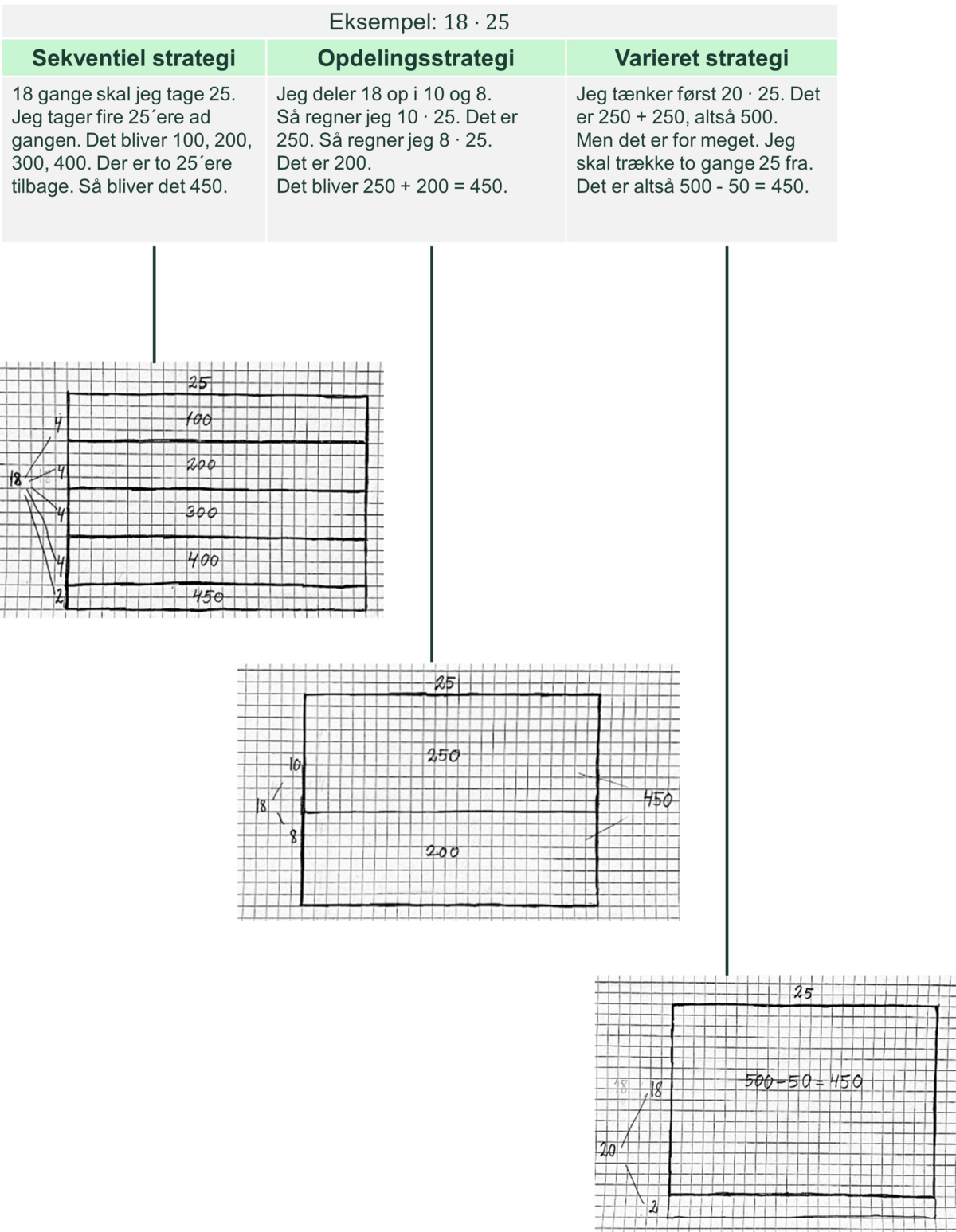
I sekventielle strategier til multiplikation er tænkningen grundlæggende baseret på gentagen addition og forbindes med bevægelser på en tallinje (Hickendorff et al., 2019).
I opdelingsstrategier er tænkningen baseret på opdelinger af en eller begge faktorer (Hickendorff et al., 2019).
Kompensationsstrategier involverer tilpasning af faktorerne og/eller beregningerne (Hickendorff et al., 2019).
ㅤ
I nogle klasser opstår de forskellige typer af strategier blandt eleverne. I andre klasser er det læreren, der bringer dem på banen i forlængelse af elevernes egne forslag. Forskning tyder på, at eleverne typisk først udvikler de sekventielle strategier, derefter opdelingsstrategier og til sidst kompensationsstrategier (Hickendorff et al., 2019).
En særlig variation af opdelingsstrategien består i at opdele de flercifrede tal i 1´ere, 10´ere (og 100´ere). Denne variation har den styrke, at den kan bruges i enhver multiplikation af flercifrede tal, og at den giver nogle forholdsvis overskuelige mellemregninger. Det er altså en strategi, som eleverne (altid) kan gribe til, hvis de ikke kan finde på en anden og mere effektiv strategi. Derfor betragtes denne form for opdeling som en strategi, der bør blive en del af alle elevers repertoire i læringssporet.
I fase 3 og 4 udvikler eleverne fortsat deres strategier til multiplikation, således at de efterhånden kan multiplicere mere og mere fleksibelt. Det implicerer, at de kommer til at råde over et repertoire af forskellige strategier, og at de i enhver beregning med multiplikation overvejer, hvilken af de strategier, de råder over, det vil være smartest for dem at vælge. Samtidig er det hensigten, at eleverne – efterhånden som de hver især er klar til det – skal udvikle måder at repræsentere deres tænkning på.
Fase 3
I fase 3 er det idéen, at eleverne arbejder i retning af mere symbolske måder at repræsentere på, ved at de ikke længere bruger rektangler med kvadratnet som støtte til deres beregninger. I stedet tegner de skitser af rektangler på almindeligt (blankt) papir. På den måde har de ikke længere mulighed for at tælle sig frem til resultaterne, men den gradvise overgang væk fra rektanglerne giver dem stadig mulighed for at forstille sig, hvordan de skitserede rektangler kunne bestå af et antal tællelige enheder.
Fase 3
At multiplicere flercifrede tal fleksibelt med støtte i skitserede rektangler og talsymboler.
Fase 4
I fase 4 er det idéen, at eleverne bliver opfordret til at slippe rektangelrepræsentationen, efterhånden som de ikke længere har brug for den. Det betyder, at eleverne ’skubbes til’ gradvist at bevæge sig fra at bruge rektangler og talsymboler til at bruge regneudtryk og omskrivninger som støtte for deres tænkning. I denne forbindelse er det vigtigt at være opmærksom på, at eleverne i en klasse næppe på samme tid er klar til et skifte fra at tænke med støtte i billedlige repræsentationer til at tænke med støtte i regneudtryk og omskrivninger. Skiftet bør komme, når den enkelte elev ikke længere har behov for rektangel-repræsentationen. På den anden side foretager den enkelte elev formentlig ikke et sådant skifte på eget initiativ. Der er behov for, at læreren introducerer regneudtryk som måder at symbolisere elevernes matematiske tænkning på. Eleverne må have mulighed for at skabe mening i regneudtrykkene og for selv at bruge sådanne måder at symbolisere dem på.
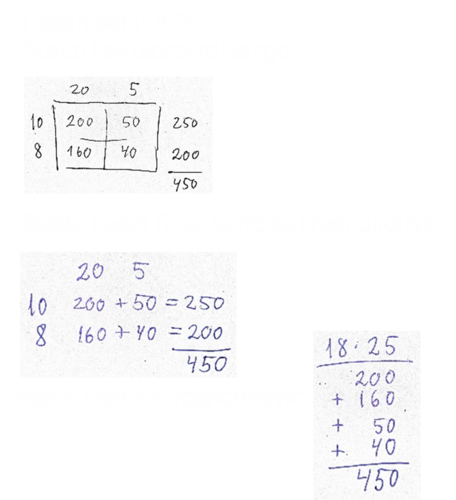
I begyndelsen kan elevernes regneudtryk fungere som en slags ’forlænget hukommelse’ for dem. De er ikke nødvendigvis sammenhængende og overholder ikke nødvendigvis formelle regler. Læreren kan guide eleverne til gradvist at skrive regneudtryk, der afspejler deres egen tænkning, og hvor de matematiske tegn er brugt rigtigt. De følgende to eksempler antyder, hvordan elevernes brug af skitserede rektangler gradvist – med lærerens støtte – kan udvikle sig til brug af regneudtryk.

Fase 4
At multiplicere flercifrede tal fleksibelt med støtte i skitserede rektangler og regneudtryk.
Regneudtrykkene nederst i eksemplerne herover viser såkaldte talbaserede metoder, der kan bruges i enhver multiplikation med tocifrede tal, og metoderne kan udvides til multiplikationer med flere cifre. Den ene metode skrives vandret, og den anden skrives lodret, men den grundlæggende idé i begge metoder er, at den ene eller begge faktorer opdeles i tiere og enere. De bygger altså på en opdelingsstrategi. Metoderne kan varieres, så enten den ene eller begge faktorer opdeles. Bemærk, at beregningerne ikke behøver at blive gennemført i en bestemt rækkefølge.
Den lodrette skrivemåde giver godt overblik over tallene, der skal adderes, men den vandrette har større sammenhæng med de algebraiske udtryk, eleverne kommer til at bruge senere i deres skoleforløb.
I læringssporet er det hensigten, at enten den ene eller den anden metode kommer til at udgøre en del af elevernes repertoire af strategier. For læreren er det vigtigt at være opmærksom på, at den metode, som vælges, ikke fremstår som en opskrift, der er afrevet fra elevernes forståelse, men snarere som et produkt, der ligger i naturlig forlængelse af en opdelingsstrategi. Metoden er grundlæggende svar på spørgsmålet: Findes der en måde at dele op på, som vi kan bruge til et ethvert flercifret tal? Da metoden kan bruges til ethvert flercifret tal, giver den eleverne mulighed for at vælge den i de situationer, hvor de ikke kan finde på en smartere beregning.
Den metode, eleverne lærer, udgør ikke et afsluttende mål for læringssporet. Som tidligere beskrevet er målene derimod, at eleverne kommer til at multiplicere fleksibelt på grundlag af forståelse. Elever, der råder over et stort repertoire af strategier, de forstår, og som vælger en strategi, der er hensigtsmæssig for dem i et givent multiplikationsproblem, opfylder derfor i højere grad målene end en elev, der konsekvent vælger en bestemt metode. Eksemplerne herunder viser regneudtryk, der bygger på andre mulige strategier til beregningen af 18∙25.
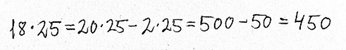
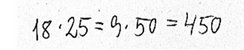
Cifferbaserede metoder indgår ikke i læringssporet.
En metode til multiplikation er en på forhånd fastlagt strategi og skrivemåde, der kan bruges til multiplikation generelt. I cifferbaserede metoder deler man fx 83 op i 8 og 3 uden at tænke på, at 8 repræsenterer et antal tiere. I talbaserede metoder ser man derimod på den værdi cifrene repræsenterer, fx ses 8 i 83 som 80 (Hickendorff et al., 2019).