Praksis – At multiplicere flercifrede tal
De tidsmæssige rammer
I nogle klasser vil det være passende at begynde læringssporet i slutningen af 3. klasse. I andre klasser vil det være bedre at vente til starten af 4. klasse.
I de fleste klasser vil det være hensigtsmæssigt at lade læringssporet strække sig over flere undervisningsforløb. Det kan fx dreje sig om to forløb á 3 uger på tværs af to skoleår, fx 4. klasse og 5. klasse.
Opdelingen mellem de to forløb kan være efter fase 2 eller efter fase 3. Hvis opdelingen er efter fase 3, vil det være en god idé at gentage dele af 3. fase, sådan at det nye forløb begynder med yderligere fokus på udvikling af fleksible og effektive strategier.
I hvert forløb kan det være en god idé at supplere det faglige indhold med øvelser fx i form af lege og spil, der giver eleverne mulighed for fortsat at få rutine i etcifret multiplikation.
Fagligt udgangspunkt
Multiplikation af flercifrede tal bygger videre på tidligere undervisning – især på elevers tidligere arbejde med multiplikation af etcifrede tal. Oversigtenviser lidt mere specifikt fire forudsætninger, som læringssporet bygger på.
For det første er det en forudsætning, at eleverne har kendskab til forskellige multiplikative situationer med etcifrede tal. Eleverne bør altså på forhånd have arbejdet med forskellige hverdagsproblemer, der kan løses med etcifret multiplikation. Det er en fordel, hvis de kan skrive gangestykker, der passer til sådanne hverdagsproblemer, og hvis de - omvendt - kan formulere hverdagsproblemer, der passer til gangestykker.
For det andet er det en forudsætning, at eleverne i et vist omfang har udviklet strategier til etcifret multiplikation. En af boblerne på oversigten antyder en sådan strategi. I boblen står et citat fra en elev, der bruger fordoblinger til at regne stykket 4 ∙ 6. En anden elev, der kan huske, at 5∙6 er 30, kunne evt. have fundet resultatet i den samme opgave ved at tænke, at 4∙6 er 6 mindre end 30.
For det tredje er det en forudsætning, at eleverne kan huske nogle resultater af etcifret multiplikation. Især er det hensigtsmæssigt, at eleverne kan huske resultaterne af multiplikation, hvor 2, 5 og 10 indgår. De udenadlærte resultater giver et grundlag, som eleverne kan bruge i deres udvikling af strategier, sådan som det antydes i forrige afsnit.
For det fjerde er det en forudsætning, at eleverne har visse erfaringer med vores titalssystem. Specielt med den egenskab, at tallene kan opdeles i 1´er, 10´ere, 100´er. Eleverne bør således have arbejdet med de naturlige tal op til 1000, før de begynder læringssporet. Desuden er det en fordel, hvis eleverne har opdaget, hvordan naturlige tal ’rykker en plads’ i vores talsystem, når man multiplicerer med 10, og to pladser, når man multiplicerer med 100.
Fase 1
Fase 1 kan fx vare en uge (4 lektioner) og går ud på, at eleverne – ud fra deres forskellige forudsætninger – løser hverdagsproblemer med multiplikation. Den primære hensigt er, at eleverne begynder at udvikle strategier til at løse sådanne problemer med støtte i konkrete materialer og/eller egne tegninger.
Problemerne bør være knyttet til en kontekst, som eleverne kan forestille sig, og som giver dem rige muligheder for at bruge konkrete materialer eller egne tegninger som støtte. Desuden skal problemerne være så udfordrende for eleverne, at de ikke kan løse dem med hovedregning alene – der skal helst være en grund til at lede efter ’smarte’ måder eller genveje til løsninger. Den type udfordring får eleverne typisk, hvis opgaven kræver multiplikation af et tocifret tal med et et- eller to cifret tal, uden at læreren på forhånd har fortalt, hvordan opgaven kan løses.
Eksempel:
Fase 1
At løse hverdagsproblemer, der involverer flercifret multiplikation med støtte i konkrete materialer og tegninger.
Den rektangulære terrasse
En familie vil bygge en (rektangulær) terrasse. Terrassen skal have 12 kvadratiske fliser på den ene led og 15 kvadratiske fliser på den anden led. Hvor mange fliser skal familien bruge i alt?
Læreren kan fx sætte scenen ved at fortælle om, hvordan familien har valgt fliser til en terrasse og aftalt, hvilken form terrassen skal have, og hvor stor den skal være. Han kan tegne en (kvadratisk) flise på tavlen og påbegynde tegningen af terrassen, så eleverne kan se for sig, hvilken form den skal have, og hvordan de kvadratiske fliser skal ligge på rad og række. Det er en del af iscenesættelsen, at klassen afklarer fagord som ’kvadrat’, ’rektangel’ og evt. ’sidelængder’.
Eleverne arbejder herefter alle i smågrupper med problemet, fx 15-20 minutter. Grupperne bør have ternet papir og tællematerialer, fx centicubes, til rådighed. Det er godt, hvis alle grupper – eller stort set alle – når til et bud på resultatet. De grupper, der bliver hurtigt færdige, kan evt. arbejde med udvidelser af opgaven. Hvad nu, hvis familien hellere vil have en terrasse, der har 15 fliser på både den ene og den anden led? Undervejs observerer læreren, hvilke strategier eleverne bruger, og han støtter og udfordrer dem, fx ved at komme med forslag, der ligger i forlængelse af elevernes egne tanker.
En elevgruppe begynder arbejdet med at tegne terrassen på ternet papir og tælle en flise ad gangen. Læreren anerkender, at elevernes fremgangsmåde kan føre dem til det rigtige resultat, men siger også, at det godt nok er mange fliser at tælle. Han spørger også, om det kan være en idé for dem at tælle flere fliser ad gangen, fx 5, 10, 15, osv.
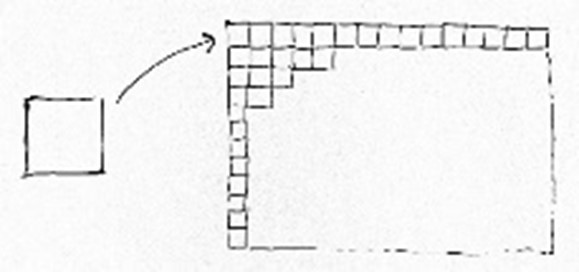
I den efterfølgende klassesamtale sigter læreren primært på at give eleverne mulighed for at udvide deres indsigt i forskellige (begyndende) strategier til multiplikation. Han har undervejs i gruppearbejdet udvalgt en gruppe, som har brugt en sekvensstrategi, og en gruppe, der har brugt en opdelingsstrategi. Han beder de to grupper præsentere deres arbejde (i den rækkefølge), fordi han tænker, at en diskussion af deres arbejde vil give klassen de tilsigtede læringsmuligheder.
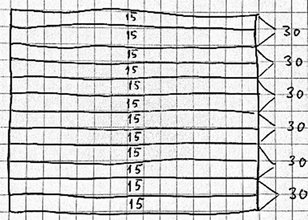
Den første gruppe fortæller, hvordan de har fundet frem til resultatet ved at ’plusse’ 15 tolv gange. De fortæller også, at de undervejs opdagede, at de i stedet for kunne ’plusse seks 30´ere’ sammen, fordi 15+15 er 30. Læreren repræsenterer elevernes forklaringer ved at markere de antal og beregninger, de fortæller om, i et (12 x 15) kvadratnet.
Klassen diskuterer, om alle er enige i, at man kan finde antallet af fliser på den måde, elevgruppen fortæller om. De diskuterer også, om de kunne gøre beregningerne endnu lettere, hvis de havde samlet ’30'erne to og to’ til ’tre 60'ere’.
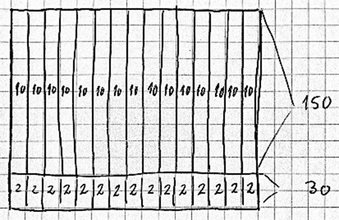
Den anden gruppe fortæller, at de har skudt genvej ved at dele terrassen op og tælle 10, 20, 30… På den måde kom de op på 150. Så manglede de bare at tælle 2, 4, 6, … og til 30. I alt fik de det til 180. Læreren repræsenterer også denne gruppes forklaringer med markeringer i et kvadratnet.
Klassen diskuterer, om alle er enige i, at man kan finde antallet af fliser på den måde, elevgruppen fortæller om. De diskuterer også, om det kunne være en god idé at dele terrassen på andre måder.
Det eksempel på et hverdagsproblem, der er omtalt her, er knyttet til den multiplikative situation, der kaldes rektangulære mønstre. I fase 1 indgår også hverdagsproblemer, der er knyttet til andre multiplikative situationer, men det er rektangulære mønstre, der former overgangen til fase 2.
Fase 2
Fase 2 kan fx vare to uger (8 lektioner) og går ud på, at eleverne – ud fra deres forskellige forudsætninger – multiplicerer tocifrede tal med støtte i en rektangel-repræsentation. Den primære hensigt er, at eleverne kan bruge rektangel-repræsentationen som støtte til at udvikle deres strategier til multiplikation.
I fase 1 udgjorde det kvadrerede rektangel en repræsentation af et hverdagsproblem som fx fliseproblemet. På tilsvarende vis kunne rektanglet udgøre en repræsentation af andre situationer med rektangulære mønstre, fx vedrørende en æske med chokolade, sæder i en biograf eller antal vinduer i et højhus. I fase 2 udgør rektangel-repræsentationen derimod en støtte til at multiplicere i en ren matematisk kontekst.
Når eleverne har løst flere hverdagsproblemer, der let kan forbindes med en rektangel-repræsentation, kan læreren introducere repræsentationen i sammenhæng med ’ren’ antalsbestemmelse, som fx:
Fase 2
At multiplicere flercifrede tal med støtte i rektangler med kvadratnet og talsymboler.
Kvadratnettet

ㅤ
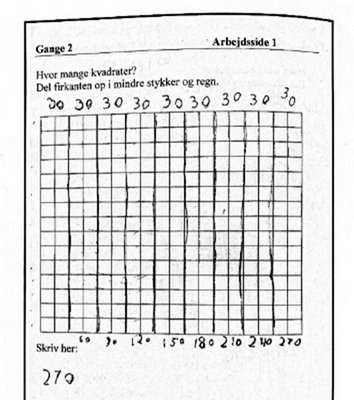
I lærerens iscenesættelse finder klassen i fællesskab ud af, at kvadratnettet i opgaven repræsenterer 15∙18. Elevernes opgave er at finde resultatet af dette stykke ved hjælp af kvadratnettet – de må selv bestemme hvordan. Måske kan de finde på nogle smarte måder?
Eleverne arbejder i cirka 20 minutter alene eller i smågrupper med opgaven. De går helt forskelligt til den. For nogle elever er den primære metode optællinger. De tæller enten et felt ad gangen eller skiptæller (fx 2, 4, 6, …). Andre elever skyder genvej ved at dele rektanglet op i 2 eller 4 lige store områder, så de kan nøjes med at tælle halvdelen eller en fjerdedel af felterne og ’skalere op’ ved at lægge det antal, de har optalt, sammen 2 eller 4 gange. En stor del af eleverne deler imidlertid rektanglet op i mindre dele. Nogle af disse elever udnytter en regelmæssighed, de har set i rektanglet, fx at der er 15 små kvadrater i hver kolonne eller 30 i to kolonner – som det kan ses på eksempel (1). Disse ’runde tal’ kan gøre beregningerne lettere for en del elever – i hvert fald lettere, end hvis opdelingerne virker mere tilfældige – som det kan ses på eksempel (2).
I den efterfølgende klassesamtale fokuserer klassen på ligheder og forskelle mellem de forskellige strategier, som eleverne udveksler. De diskuterer også, hvilke strategier der er smarte i forhold til den konkrete beregning. Klassesamtaler som denne kan bl.a. give eleverne mulighed for at indse, at:
- alle stykker altid kan opdeles på forskellige måder.
- hvis man fordobler antallet af opdelinger, så bliver der halvt så mange tern i hver opdeling. Fx kan $9 \cdot 20$ opdeles i 9 felter á 20 eller 18 felter á 10, dvs. $9 \cdot 20 = 18 \cdot 10$.
- i nogle stykker kan man bruge halveringer. Fx kan $16 \cdot 12$ først deles op i to lige store felter, dvs. $16 \cdot 12 = 2 \cdot 8 \cdot 12$. Derefter kan hvert af de nye felter igen opdeles i to lige store felter, dvs. $2 \cdot 8 \cdot 12 = 4 \cdot 8 \cdot 6$, osv.
- i nogle stykker kan det betale sig først at ’regne for meget’ og så bagefter trække det overskydende fra. Fx kan man i stedet for $19 \cdot 14$ regne $20 \cdot 14$ og så trække 14 fra, dvs. $19 \cdot 14 = 20 \cdot 14 - 1 \cdot 14$.
Arbejdet i fase 2 fortsætter i samme tråd med, at eleverne løser forskellige multiplikationsstykker med støtte i rektangel-repræsentationer. De første stykker har læreren på forhånd tegnet på arbejdsark til hver elev, for at de kan fokusere på strategierne. Senere er det en del af elevernes opgave selv at tegne rektangel-repræsentationen på ternet papir ud fra givne gangestykker inden for talområdet 10-20. På den måde får eleverne mulighed for at fokusere på, hvordan regneudtrykket hænger sammen med tegningen af rektanglet.
Fase 3
I fase 3 skal eleverne fortsat arbejde med strategier til multiplikation, og de skal gradvist slippe rektangelmodellen i forbindelse med beregningerne. Hensigten er dels, at eleverne skal komme til at multiplicere fleksibelt, dels at de – efterhånden som de bliver klar til det – skal komme til at opfatte regneudtryk som objekter, de kan ’tænke i’. For læreren er det vigtigt at være opmærksom på, at eleverne bevarer forståelsen af de beregninger, de foretager, selv om de ikke længere (nødvendigvis) bruger rektangelmodellen på samme måde som tidligere.
Eleverne arbejder fortsat med at multiplicere tocifrede tal – og for nogle elevers vedkommende evt. også trecifrede. I klassesamtaler udveksler og diskuterer eleverne deres forskellige strategier med fokus på ligheder, forskelle og ’smarte måder’. Læreren må sikre sig, at eleverne får mulighed for at lære både sekventielle strategier, opdelingsstrategier og kompensationsstrategier.
En særlig variation af opdelingsstrategien består i at opdele de flercifrede tal i enere, tiere osv. som beskrevet i afsnittet om tilgangen i læringssporet. Hvis den ikke opstår blandt eleverne, bør læreren (også) præsentere denne idé, hvor opdelingerne harmonerer med talsystemets opbygning.
En central del af fase 3 består i, at eleverne for hver af de beregninger, de arbejder med, bliver vant til at vælge hensigtsmæssigt blandt de strategier, de kan. Det kan bl.a. foregå ved, at eleverne arbejder ’omvendt’, sådan at de for en udvalgt strategi skal foreslå gangestykker, som strategien vil være god til. Man kan fx forestille sig, at elever i forbindelse med kompensationsstrategier vil pege på 99∙47 og 198∙34 som eksempler på gangestykker, hvor det godt kan betale sig først at beregne hhv. 100∙47 og 200∙34 og efterfølgende kompensere.
For at ’skubbe’ i retning af at slippe rektangelmodellen kan læreren opfordre eleverne til at (prøve at) regne på blankt papir i stedet for på ternet papir, når de multiplicerer store tal. Den nye måde at repræsentere på kræver, at elever i højere grad kan ’tænke i talsymboler’, fordi kvadratnettet, der kan støtte beregninger, fx igennem optælling eller skiptælling, er væk (se illustrationen på oversigten).
Nogle elever beskriver, hvordan de klarer udfordringen: ’Jeg forestiller mig, at ternene er der, selv om de er væk. Jeg ved fx, at når der står 10 på mit stykke, så betyder det 10 tern’. Efterhånden som eleverne vænner sig til, at kvadratet er væk, kan man se, at deres rektangler bliver mere og mere skitserede. De er ikke længere målfaste, og måske ’forsvinder’ kanten mere og mere på dem.
Eleverne behøver ikke nødvendigvis at slippe rektangel-repræsentationen på samme tid. For nogle kan det være en fordel at holde fast i ternene i længere tid, fx fordi de stadig i nogen grad har brug for at tælle sig frem. Læreren kan fx ´skubbe´ disse elever ved at give opgaver, der på den ene side er besværlige at tegne, fordi faktorerne er forholdsvis store tal. På den anden side bør opgaverne være forholdsvis lette at regne uden optællinger. Det kan fx være 15∙21 eller 12∙25. En anden strategi kan være at lade eleverne lave en kopi på blankt papir af en beregning, de først har lavet på ternet papir. Det giver dem mulighed for at sammenligne og se ligheder og forskelle mellem de to repræsentationer.
Fase 3
At multiplicere flercifrede tal fleksibelt med støtte i skitserede rektangler og talsymboler.
Fase 4
Fase 4 handler om i højere og højere grad at inddrage regneudtryk som en repræsentation, eleverne kan støtte sig op ad i beregninger. Hensigten er, at eleverne gradvist skal vænne sig til at ’tænke i’ tal og regnetegn.
For eleverne kan skiftet bestå i, at de opfordres til helt at holde op med at tegne rektanglet, når det ikke længere er nødvendigt for dem. Nogle elever kommer på baggrund af denne opfordring selv med forslag til en skrivemåde, der repræsenterer de samme beregninger som tidligere i læringssporet, men som kun består af talsymboler, regnetegn og evt. lighedstegn. Andre elever kan støttes med forslag til regneudtryk, der efterhånden går i retning af dem, der er eksemplificeret i afsnittet ’Tilgang’ og på oversigten. Læg mærke til, at udtrykkene kan se ud på forskellige måder, men at alle disse måder er tæt knyttet til rektangelmodellen.
Bemærk også, at overgangen til regneudtryk ikke nødvendigvis skal ske samtidig for alle børn – og at det altid er en mulighed at bevæge sig tilbage i læringssporet, sådan at alle elever får mulighed for at udvikle metoder i takt med, at de udvikler deres forståelser og færdigheder. I klassen kan eleverne på samme tid bruge flere forskellige måder at repræsentere på. Nogle elever bruger fortsat skitserede rektangler og talsymboler. Andre har sluppet dem helt og bruger kun omskrivninger af regneudtryk.
Fase 4
At multiplicere flercifrede tal fleksibelt med støtte i skitserede rektangler og regneudtryk.