Tilgang – At behandle algebraiske udtryk
Progression
Læringssporet bygger på tre principper for progression:
For det første tager det udgangspunkt i problemer, som eleverne kan beskrive og undersøge med matematik, de kender. Der kan både være tale om hverdagsproblemer og rene matematiske problemer. Igennem sporet flytter fokus sig gradvist fra disse problemer til matematiske udtryk, som eleverne kan arbejde med uafhængigt af det oprindelige udgangspunkt.
For det andet er der i begyndelsen af læringssporet fokus på udtryk med specifikke tal, men senere i læringssporet flytter fokus til udtryk med bogstaver som repræsentationer for variable. Der er med andre ord en progression fra det specifikke og konkrete i retning af det generelle og abstrakte.
For det tredje er der igennem læringssporet en progression fra fokus på algebraiske udtryk, der er koblet til beregninger, til algebraiske udtryk, der udgør resultater af beregninger. I den første halvdel af læringssporet kan elever fx arbejde med at opstille algebraiske udtryk, som beskriver, hvordan man kan beregne arealet af de to rektangler, der er vist på Figur 3. De udtryk, eleverne opstiller, er på den måde koblet til beregninger. Sidst i læringssporet kan eleverne arbejde med at sammenligne de to arealer, fx ved at subtrahere udtrykkene. I den forbindelse må de opfatte de samme udtryk som resultater af beregninger, dvs. som udtryk for rektanglernes arealer. Resultatet af subtraktionen bliver også et algebraisk udtryk. I modsætning til tidligere repræsenterer udtrykket ikke selve beregningen, men resultatet af den; nemlig arealforskellen.
I 6.-9. klasse bør eleverne gennemarbejde læringssporet med alle 4 faser flere gange, fx en gang på tre af klassetrinene. Hvert gennemløb svarer til et forløb af fx 3 ugers varighed, hvor der sættes fokus på udvalgte regneregler for reelle tal. Samlet set bør forløbene sigte på de operationer med algebraiske udtryk, der omtalt i Tabel 1.
Rækkefølgen i Tabel 1 udgør et vejledende forslag til en rækkefølge i arbejdet med reglerne. Det er en god idé at vente med de regler, der vedrører omskrivning og regning med brøker til sidst i læringssporet.
Forskellige kontekster giver mulighed for at fokusere på forskellige regneregler. Som det fremgår af Oversigten giver kontekster, der involverer arealberegning af rektangler, fx gode muligheder for at fokusere på de distributive love og på faktorisering. Andre regler, fx addition og subtraktion af led samt ophævelse af parenteser, kan komme i spil i kontekster, der fx vedrører beregning af antal, priser, længde, vægt eller priser.
De problemer, der udgør et afsæt i læringssporet, bør dog give muligheder for at: opstille, tolke, omskrive og beregne. Her er to andre eksempler på sådanne problemer:
Eksempel 1: Indkøb
Se på indkøbslisten i Figur 4.
- Hvordan kan man beregne den samlede pris? Skriv mange forskellige regneudtryk.
- Se på hinandens regneudtryk. Hvordan kan de være tænkt?
- Sammenlign hinandens regneudtryk. Kan I (næsten) uden at regne se, at de viser den samme udregning?
- Udregn hvert udtryk. Får I samme resultat?
Eksempel 2: Biograf
Se på oversigten af biografsalen i Figur 5.
- Hvordan kan man beregne antallet af sæder? Skriv mange forskellige regneudtryk.
- Se på hinandens regneudtryk. Hvordan kan de være tænkt?
- Sammenlign hinandens regneudtryk. Kan I (næsten) uden at regne se, at de viser den samme udregning?
- Udregn hvert udtryk. Får I samme resultat?


Fase 1
I fase 1 arbejder eleverne med udtryk, der har specifikke tal. Udgangspunktet kan være en aktivitet, der giver mulighed for at opstille forskellige regneudtryk for den samme størrelse:
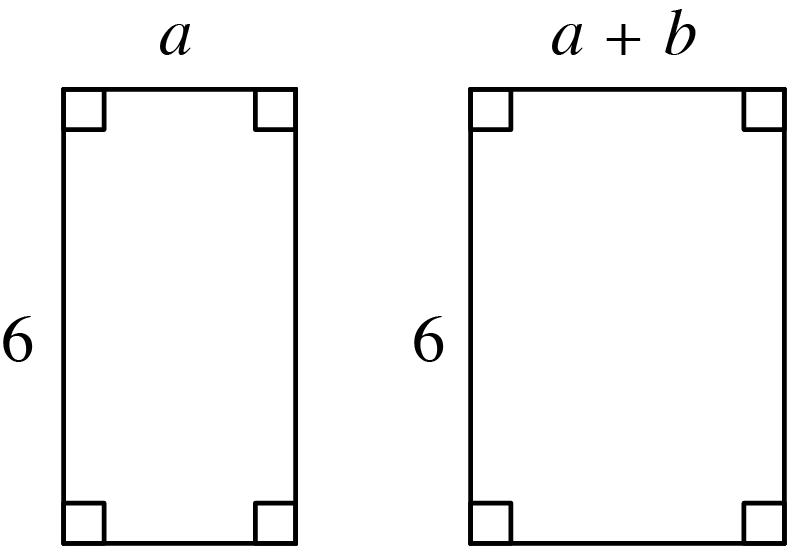
Eksempel 3: Plantegninger af nye huse
Figur 6 viser en plantegning af et hus med tilhørende garage.
Tegningen er lavet på et kvadratnet.
Jeres opgave er at skrive mange forskellige regneudtryk, som man kan bruge til at beregne husets og garagens samlede areal.
Fase 1
At opstille, tolke, omskrive og foretage beregninger med regneudtryk.

De forskellige udtryk, som eleverne opstiller (fx på basis af aktiviteten i eksempel 3), samles i klassen og bearbejdes på tre forskellige måder:
1) Tolkning
Eleverne tolker udtrykkene i forhold til det, de repræsenterer. Hvordan hænger det sammen?
I tilknytning til eksempel 3 kan eleverne fx beskrive, hvordan udtryk som
$12 \cdot 8 + 4 \cdot 3$
$(4+8) \cdot 8 + 4 \cdot 3$
$4 \cdot 11 + 8 \cdot 8$
$4 \cdot (8 + 3) + 8^2$
hænger sammen med plantegningen og arealet af huset og garagen.
2) Omskrivning
Eleverne omskriver udtrykkene for at sammenligne dem og undersøge, om de udtrykker den samme størrelse.
I tilknytning til eksempel 1 kan eleverne fx ved at bruge viden om parenteser og potenser argumentere for, at $4 \cdot 11 + 8 \cdot 8$ og $4 \cdot (8+3) + 8^2$ udtrykker samme værdi.
3) Beregning
Eleverne beregner værdien af udtrykkene. Giver de samme resultat?
I tilknytning til eksempel 1 medfører dette punkt bl.a., at eleverne overholder regningsarternes hierarki.
Bemærk, at en kobling til den geometriske repræsentation kan støtte udregningen.
Fase 2
I fase 2 arbejder eleverne med algebraiske udtryk. Det er vigtigt, at aktiviteterne i denne fase bygger direkte videre på konteksterne i fase 1, så eleverne kan basere sig på deres erfaringer med specifikke tal, når de i fase 2 skal arbejde med algebraiske udtryk. Disse algebraiske udtryk bør for eleverne forekomme som generaliseringer af regneudtryk.
Eksempel 4: Flere plantegninger i én
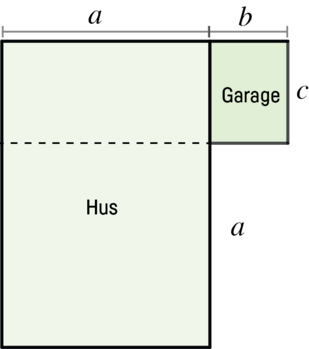
Firmaet BYG bygger mange huse med garager efter modellen, der er vist som plantegning i Figur 7. Længderne $a$, $b$ og $c$ kan være forskellige fra hus til hus. Jeres opgave er at skrive udtryk, man kan bruge til at beregne det samlede areal af hus og garage. Prøv at finde forskellige udtryk.
Fase 2
At opstille og tolke algebraiske udtryk.
Et regneudtryk er en forbindelse af tal, regnetegn og evt. andre symboler som lighedstegn og parenteser.
I iscenesættelsen af aktiviteten i eksempel 4 kan en klasse skrive forskellige eksempler på længder, $a$, $b$ og $c$ kan have. De kan også diskutere, hvilke afgrænsninger der er realistiske for hver af de tre variable (længden $b$ skal fx være større end bredden på en bil, hvis det grå område på plantegningen skal fungere som garage). Det er vigtigt, at eleverne kommer til at opfatte bogstaverne som repræsentationer for forskellige længder, og at de ved, at et bogstav ikke kan repræsentere to forskellige værdier på samme tid.
Når de efterfølgende opstiller (helst) flere udtryk, der beskriver arealet af bygningen, kan de evt. støtte sig op ad deres regneudtryk fra eksempel 1.
De forskellige udtryk, som eleverne opstiller, samles i klassen og bearbejdes på to forskellige måder:
1) Tolkning
Eleverne tolker udtrykkene ift. det, de repræsenterer. Hvordan hænger det sammen?
I tilknytning til eksempel 3 kan eleverne fx beskrive, hvordan udtryk som
$a^2 + c \cdot (a+b)$
$a \cdot (a + c) + b \cdot c$
$(a+b) \cdot (a + c) - a \cdot b$
hænger sammen med plantegningen og arealet af huset og garagen.
2) Sammenligning
Eleverne sammenligner de algebraiske udtryk med de udtryk regneudtryk, de tidligere har opstillet. Hvilke udtryk har samme form?
Hvis eleverne både har arbejdet med eksempel 3 og 4, kan de fx se, at udtrykkene $4 \cdot (8+3)+8^2$ og $a^2+c \cdot (a+b)$ ligner hinanden, fordi de består af samme type led. Eleverne kan opstille flere regneudtryk, der har samme form som det algebraiske udtryk (altså med andre værdier for $a$, $b$ og $c$, som læreren foreslår). På den måde får de mulighed for at opfatte det algebraiske udtryk som en generalisering af en mængde af regneudtryk.
Fase 3
Denne fase fokuserer på omskrivninger af de algebraiske udtryk, eleverne har opstillet i fase 2. Eleverne ved allerede, at de forskellige udtryk repræsenterer den samme størrelse. Ved at omskrive udtrykkene får eleverne endnu en begrundelse for, at udtrykkene har samme værdi. Denne begrundelse bygger generelt på regneregler for de reelle tal – i eksempel 3 vedrører omskrivningerne primært den distributive lov.
Udtrykket $a^2+ c \cdot (a+b)$ kan fx omskrives til $a^2 + a \cdot c + b \cdot c$. På tilsvarende vis kan udtrykket $a \cdot (a + c) + b \cdot c$ omskrives til $a^2 + a \cdot c + b \cdot c$. Det medfører, at $a^2 + c \cdot (a+b)$ og $a \cdot (a + c) + b \cdot c$ har samme værdi.
Eleverne får mulighed for at se mening i omskrivningerne (og dermed i regnereglerne), når de kobles til det, udtrykkene repræsenterer. Den øverste del af illustrationen fra eksempel 3 (se figur 8) illustrerer fx, at $c \cdot a + b = a \cdot c + b \cdot c$.
I tillæg kan brugen af eksempler bidrage til at overbevise eleven om omskrivningernes og regnereglernes rigtighed. Hvis $a=8$, $b=3$ og $c=5$, viser ovenstående beregning fx, at $5 \cdot (8 +3) = 40 + 15 = 55$.
Fase 3
At omskrive algebraiske udtryk.

Fase 4
I fase 4 foretager eleverne beregninger med algebraiske udtryk. I konteksten med plantegninger kan sådanne beregninger fx blive aktuelle, hvis eleverne skal addere, subtrahere, multiplicere eller dividere udtryk, der repræsenterer arealer.
I tilknytning til eksempel 3 kan man fx forestille sig, at eleverne får til opgave at multiplicere arealet af grundplanen med 2 for at beregne det samlede arealet af et hus med en 1. sal. En anden mulighed er, at eleverne skal addere et udtryk for arealet af en tilbygning til arealet af grundplanen. Subtraktion og division kan fx komme ind i billedet, hvis eleverne skal sammenligne to arealer.
Hvis arealet af hustype 1 er $2a \cdot b$, og arealet af hustype 2 er $a \cdot b$, så er forskellen mellem de to arealer $2ab - ab = ab$, og hustype 1 er $\frac{2ab}{ab}=2$ gange større end hustype 2.
I fase 4 er det et mål, at eleverne kan regne med de algebraiske udtryk uafhængigt af det, udtrykkene repræsenterer. Så længe, der er behov for det, kan elevernes beregninger dog støttes af geometriske repræsentationer og konkrete eksempler. Figur 9 kan fx støtte eleverne i at se mening i beregningerne $2ab-ab=ab$ og $\frac{2ab}{ab}=2$.
Igennem både fase 3 og 4 kan og bør læringssporet suppleres med aktiviteter, som giver eleverne mulighed for at få rutine med at bruge de regneregler, de arbejder med, samtidig med at de giver ’stof til eftertanke’, dvs. tilføjer en begrebsmæssig dimension til arbejdet med at opnå en vis rutine i at bruge regnereglerne fra Tabel 1. Eksempler på sådanne øvelser indgår i det følgende afsnit om læringssporet i praksis.
Fase 4
At foretage beregninger med algebraiske udtryk.
