At behandle algebraiske udtryk
Introduktion
Dette læringsspor retter sig mod arbejdet med algebraiske udtryk i 6.- 9. klasse. Set i forhold til stofområdet ’tal og algebra’ i grundskolen vedrører det udtryk, ligninger og funktioner (som vist på Figur 1 herunder).
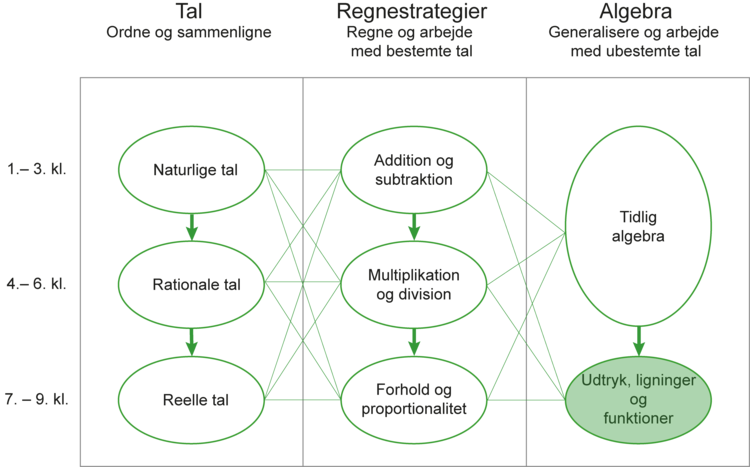
Læringsspor til grundskolen udviklet af NCUM under den fælles indsats for tal og algebra.
Udgivet 2025
Mål
Læringssporet skal bidrage til, at eleverne bliver i stand til at behandle algebraiske udtryk, dvs. opstille, tolke, omskrive og foretage beregninger med udtrykkene på baggrund af viden om regler for beregninger med reelle tal.
Elever, der er kommet langt i forhold til målet, kan fx opstille et algebraisk udtryk, der beskriver arealet af Figur 2 herunder, og forklare, hvordan hvert led i deres udtryk hænger sammen med figuren. De kan med omskrivning afgøre, om andre udtryk repræsenterer det samme areal, og de kan udtrykke det samlede areal af tre kongruente figurer ved enten at addere deres udtryk tre gange eller ved at multiplicere deres udtryk med 3.
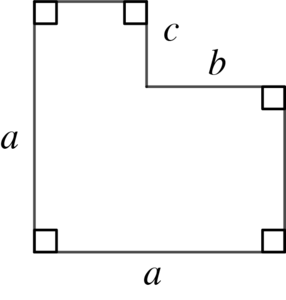
Udtryk A: $a(a-b)+b(a-c)$
Udtryk B: $a^2-bc$
Omskrivning: $a(a-b)+b(a-c)=a^2-ab+ab-bc=a^2-bc$
Arealet af tre kongruente figurer: $3(a^2-bc)=3a^2-3bc$
Et algebraisk udtryk er en kæde af tal og andre symboler, herunder bogstaver, der symboliserer (evt. forskellige typer af) variable.