Praksis – At behandle algebraiske udtryk

De tidsmæssige rammer

Læringssporet kan strække sig over fx tre år inden for 6. - 9. klasse. Som beskrevet i afsnittet ’Tilgang’ gentages de fire faser flere gange, fx én gang på 6., 7. og 8. klassetrin. Hvert gennemløb kan udgøre et forløb på fx 3 uger.

I hvert forløb fokuseres på udvalgte regneregler fra listen i afsnittet Progression. Hensigten er, at de tre forløb tilsammen skal dække alle de nævnte regneregler.

Det faglige udgangspunkt

Det er en forudsætning, at eleverne før dette læringsspor har arbejdet med både naturlige tal, hele tal og rationale tal i forskellige sammenhænge. De bør altså bl.a. have begreb om negative tal og brøker, herunder brøker med samme værdi.

Det er også en forudsætning, at eleverne har erfaringer med de fire regningsarter og regningsarternes hierarki. De skal bl.a. kunne forbinde forskellige situationer med hver regningsart og kunne opstille og udregne regneudtryk, hvori der indgår flere led og flere regningsarter.

Introduktion

Oversigt

Tilgang

Praksis

Grundlag

Tal og algebra

Fase 1

Som beskrevet i afsnittet ’Tilgang’ tager læringssporet udgangspunkt i problemer, som eleverne kan undersøge og beskrive med matematik, de kender, dvs. med specifikke tal og regneudtryk.

I den følgende episode iscenesætter en lærer et problem, der handler om antallet af sæder i en biograf. Episoden illustrerer, hvordan læreren i iscenesættelsen kan spore eleverne ind på at opstille regneudtryk, der er forbundet med en kontekst.

Fase 1

At opstille, tolke, omskrive og foretage beregninger med regneudtryk.

Sæder i en biograf

Lærer: I har nok alle sammen prøvet at være I biografsale, som er store, og biografsale, der er små. Hvor mange sæder, tror I, der har været i de mindste biografsale, I har set? Hvor mange sæder, tror I, der har været i de største biografsale, I har set?

Elever: (Kommer med forskellige bud og udveksler erfaringer med forskellige biografsale).

Lærer: I dag skal vi se på den biografsal, jeg har prøvet at tegne her (Se Figur 5). Kan I se, hvad der skal forestille sæder på tegningen?

Elever: Ja.

Lærer: Har I været i en biografsal, der er bygget op på samme måde med gange imellem nogle af sæderne?

Albert: Ja, det er der fx i Palads.

Beate: Ikke i alle sale.

Lærer: Ok, så nogle biografer er bygget op på denne måde. Forestil jer, at I hurtigt skal finde ud af, hvor mange sæder der er. I kan selvfølgelig tælle, men I skal prøve at skyde genvej. Med andre ord: Er der en beregning, som I kan bruge til at finde antallet af stole? (Venter)

Cecilie: Ja, altså man kan gange. Øverst til venstre er der jo fx $3 \cdot 5$ sæder…

Ditlev: Men der er jo 10 sæder hele vejen hen? Man skal vel sige $3 \cdot 10$?

Eigil: Det kommer an på, hvor meget man tæller med.

Lærer: Det kan vel godt tænkes, at der er flere måder at regne på?

Felix: Ja, man kan vel også bare bruge plus?

Eleverne får til opgave at skrive flere forskellige regneudtryk, der beskriver antallet af sæder. På den baggrund udvælger læreren følgende udtryk, fordi de giver mulighed for at samle led, når de sammenlignes. Hun skriver udtrykkene på en fælles tavle:

1) $3 \cdot 5 + 3\cdot 5 + 5 \cdot 5 + 5 \cdot 5$

2) $2 \cdot 3 \cdot 5 + 2 \cdot 5^2$

3) $3 \cdot 10 + 5 \cdot 10$

4) $8 \cdot 10$

I en fælles klassesamtale beder læreren eleverne beskrive, hvordan hvert udtryk hænger sammen med tegningen af biografsalen. Klassen bliver enige om, at alle udtryk korrekt beskriver antallet af sæder. Udtrykkene er altså forskellige måder at skrive samme værdi.

Dernæst beder læreren eleverne sammenligne de fire udtryk. Spørgsmålet er, om eleverne – uden at regne – kan begrunde, hvorfor udtrykkene har samme værdi? Eleverne kommer med forskellige bud på begrundelser. I den forbindelse støtter læreren deres sprog, bl.a. ved at genopfriske eller introducere fagord som ’led’, ’faktor’ og ’addere’. Holdbare forklaringer fra elever kan fx lyde sådan:

Cecilie: I udtryk 2) er leddene fra udtryk 1) jo på en måde bare samlet. Der er jo to led, hvor der står $3 \cdot 5$. Det svarer til $2 \cdot 3 \cdot 5$. På samme måde er det med de led, hvor der står $5 \cdot 5$. Det er jo det samme som $5^2$ , og så er de bare samlet til $2 \cdot 5^2$ .

Lærer: Ok. Du taler om at samle led. Er det rigtigt forstået, at du siger, at disse to led er samlet (peger på $3 \cdot 5 + 3 \cdot 5$), og at disse to led er samlet (peger på $5 \cdot 5 + 5 \cdot 5$).

Cecilie: Ja.

Lærer: Er I andre enige i, at man kan samle led på den måde?

Elever: Joh…

Samtalen fortsætter med flere pointer, der vedrører omskrivninger af regneudtryk. Læreren lægger bl.a. vægt på, at $3 \cdot 10 + 5 \cdot 10 = 8 \cdot 10$, da udtryk 3) og 4) har samme værdi.

Eleverne kan se på tegningen, at dette må være sandt, men læreren beder dem også argumentere ud fra tallene i udtrykket.

Albert: Der er jo 3 tiere og 5 tiere. Det er 8 tiere. 3 plus 5 er 8.

Lærer: Ok, det kan næsten lyde som en ny måde at samle led på? Her bliver to led jo også til et led. Hvad hvis der havde stået $4 \cdot 10 + 6 \cdot 10$?

Jonas: Jamen, så ville det jo ikke have passet til tegningen.

Lærer: Enig. Men er I med på kun at kigge på udtrykket her?

Albert: Det kan vi samle til $10 \cdot 10$, for der er 4 tiere og 6 tiere. 4 plus 6 er 10.

Sidst i undervisningsmodulet beder læreren eleverne om at udregne hvert stykke for at sikre, at de alle giver samme resultat. I den forbindelse taler klassen om regningsarternes hierarki.

Figur 5. Oversigt over sæder i biografsal.

Fase 2

I fase 2 foretager læreren springet fra de specifikke tal til generaliserede tal og bogstavudtryk. Det medfører også et skift i kontekst, men læreren sørger for, at den nye kontekst ligger i direkte forlængelse af den fra fase 1, så eleverne kan bygge videre på deres erfaringer.

I den følgende episode introducerer læreren den nye kontekst. Episoden illustrerer, hvordan læreren støtter skiftet fra de specifikke tal til de generaliserede tal.

Fase 2

At opstille og tolke algebraiske udtryk.

Et generaliseret tal er et tal, der repræsenterer en mængde, fx mængden af reelle tal. Et generaliseret tal udtrykkes oftest med et bogstav.

Sæder i en biograf

Lærer: I den biograf, vi snakkede om sidst, er der mange biografsale, der er opbygget på samme måde med nogle gange imellem rækkerne med sæder. Her er en tegning, der viser opbygningen (se tegning i Figur 6 til højre).

Det er lidt forskelligt, hvor store biografsalene er. Det er derfor, at jeg har skrevet bogstaver i stedet for tal. I kan se, at der står a, b og c. I må forstille jer, at hvert bogstav står for et tal. a kan fx være 5, 6, 7 eller… På samme måde er det med b og c .

Eigil: Kan a og b og c være det samme tal?

Lærer: Ja, det kan det godt... Men a kan ikke være flere forskellige tal på samme tid. Alle de steder, der står a, er der tale om det samme tal. På samme måde er det med b... Hvordan vil biografsalen egentlig se ud, hvis a, b og c er det samme tal?

Beate: Altså, fx 10?

Cecilie: Så vil der jo stå 10 alle steder.

Albert: Så bliver der ligesom nogle kvadrater i biografsalen.

Felix: Ja, altså der vil være lige så mange rækker, som der vil være sæder i hver række.

På samme måde som i fase 1 får eleverne først til opgave at opstille og tolke udtryk, der beskriver antallet af sæder. I denne fase er der imidlertid tale om algebraiske udtryk.

Eleverne kan fx opstille udtryk som:

1) $2 \cdot a \cdot b + 2 \cdot a \cdot c$

2) $b \cdot a + b \cdot a + c \cdot a + c \cdot a$

3) $b(a + a) + c(a+a)$

4) $a(b+c)+a(b+c)$

5) $(a+a)(b+c)$

På samme måde som i fase 1 tolker de udtrykkene i forhold til tegningen af biografsalen.

Figur 6. Biografsal med generaliserede mål.

Fase 3

Denne fase begynder med, at eleverne sammenligner algebraiske udtryk, som læreren har udvalgt på baggrund af elevernes opstillinger i fase 2. Læreren kan udvælge udtryk, som giver mulighed for at fokusere på udvalgte regneregler (se tabellen i afsnittet ’Progression’ under Tilgang).

I forbindelse med biografeksemplet kan man fx forestille sig, at læreren udvælger udtryk 2) og 3) fra fase 2 for at fokusere på den ene af de distributive love.

Fase 3

At omskrive algebraiske udtryk.

Sæder i en biograf

Lærer: Prøv at se på de to første led i udtryk 2) og det første led i udtryk 3).

(Skriver '$b \cdot a + b\cdot a = b(a+a)$' på tavlen)

Elever: Ja.

Lærer: Er der nogen, der vil vise på tegningen, hvorfor udtrykkene på venstre og højre side har samme værdi?

(En elev viser på tegningen, der også er på tavlen, hvordan de to udtryk beskriver det samme område på forskellige måder)

Lærer: Ok. Lad os prøve at tjekke med tal, om lighedstegnet kommer til at passe. Hvad hvis a er 5, og b er 10?

Cecilie: Så kommer der til at stå $10 \cdot 5 + 10 \cdot 5 = 10 \cdot 10$.

Lærer: Ok... Hvad hvis a er 3, og b er 4?

Eigil: Så bliver det $4 \cdot 3 + 4 \cdot 3 = 4\cdot 6$.

Jonas: Altså, hvis man først skal tage 3 fire gange og bagefter igen skal tage 3 fire gange, så kan man jo lige så godt tage 6 fire gange med det samme.

Lærer: Så de to 3'ere samler du til en 6'er? (Skriver på tavlen som i Figur 7 til højre)

Er I enige i, at man kan gøre sådan?

Elever: Joh...

Lærer: Og er I enige i, at samme sker i dette udtryk? (Tegner pile på tegningen som Figur 8 til højre)

Figur 7.

Figur 8.

I fase 3 arbejder klassen også med at omskrive de udtryk, de har opstillet og sammenlignet. Oplægget til dette arbejde kan ligge i forlængelse af sammenligningerne. Nogle af udtrykkene er kortere end andre – de har færre led. Det gælder fx udtryk 5) i eksemplet fra fase 2. De få led gør ofte udtrykkene mere overskuelige og nemmere at bruge i praksis, fx til at foretage en beregning som i eksemplet.

I omskrivningerne får eleverne brug for netop de regneregler, klassen har sat fokus på, ved at opstille, tolke og især sammenligne udtryk. I første del af læringssporet vil det være naturligt, at vægten ligger på at samle led af samme type ved at addere eller subtrahere. Det er langt fra sikkert, at klassen kan reducere hvert udtryk ’helt i bund’. I senere runder giver bl.a. faktorisering mulighed for at reducere antallet af led i udtrykkene.

Fasen kan udvides med aktiviteter, som giver eleverne mulighed for at få rutine med at bruge de regneregler, de arbejder med, samtidig med at de giver ’stof til eftertanke’. Et eksempel på en sådan aktivitet kan være:

Skriv mange forskellige udtryk, man kan reducere til a. Prøv bl.a. at finde på udtryk, der har mere end 3 led. Prøv også at finde på udtryk, der har to forskellige regningsarter, tre regningsarter og fire regningsarter.

Fase 4

I fase 4 skal eleverne foretage beregninger med algebraiske udtryk. Behovet for sådanne beregninger kan bl.a. opstå, hvis klassen ser på forskelle mellem forskellige udtryk. I forlængelse af de eksempler, der er beskrevet i det forrige, kan det fx ske sådan i en 6. eller 7. klasse:

Fase 4

At foretage beregninger med algebraiske udtryk.

Sæder i en biograf

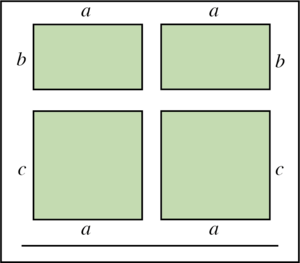
Lærer: Ejerne af den biograf, vi har snakket om, overvejer, om de skal dele nogle af deres biografsale op, så der kommer to små sale for hver af de store sale. Tegningerne til højre viser, hvordan de tænker at dele op.

Nu skal I prøve at regne ud, hvor stor forskel der bliver på antallet af pladser i den store sal og i en af de små sale.

Jonas: Det kan vi jo ikke… for vi ved ikke, hvor mange pladser der er… Det kommer jo an på, hvad $a$ og $b$ og $c$ er.

Lærer: Enig. Det kommer jo an på, hvad $a$, $b$ og $c$ er. Vi kan prøve med et eksempel. Lad os sige, at $a$ er 5, $b$ er 6, og $c$ er 7.

(Hun erstatter bogstaverne med tallene)

Prøv at bruge et par minutter på at regne ud, hvor mange sæder det giver i den store sal og i den lille sal.

(Ventetid)

Felix: Jeg har fået den store sal til 130. Jeg regner $2\cdot5\cdot6+2\cdot5\cdot7$.

Maria: Den lille sal har $65$ sæder. Det er bare $5\cdot6+5\cdot7$ .

Albert: Ja, man kan jo bare sige, at det er halvdelen af $130$.

Lise: Jeg har fået forskellen til $65$.

Lærer: Ok. Hvordan regner du det ud?

Noah: Jeg trækker bare $65$ fra $130$.

Lærer: Kan man sige, at du har regnet det her ud: $2\cdot5\cdot6 + 2\cdot5\cdot7 - (5\cdot6 + 5\cdot7)$?

Beate: Ja, det kan man godt, men det ser på en måde sværere ud, end det var.

Carla: Hvorfor skriver du parentes om tallene fra den lille sal?

Lærer: Godt spørgsmål. Det kan jeg jo lade gå videre til resten af klassen.

(ventetid)

Cecilie: Det er jo, fordi det er begge to… altså begge led… eller hele salen, man skal trække fra. Hvis der ikke stod parentes, ville $5\cdot7$ jo blive lagt til.

(Går op til tavlen og peger på plustegnet foran sidste led)

Lærer: Godt… Men nu var det et eksempel, vi regnede på. Det, vi nåede frem til, ville jo ikke passe i enhver biografsal.

Jeg vil prøve at lokke jer med på at bruge den samme tankegang sammen med bogstaverne. Kan vi opstille et udtryk, der viser forskellen mellem antal sæder i en stor sal og en lille sal?

Klassen taler sig frem til, at udtrykket $2ab + 2ac - (ab+ac)$ beskriver forskellen (differensen). I fællesskab reducerer de også udtrykket ved at hæve parentesen og samle led: $2ab + 2ac - ab + ac = 2ab + 2ac - ab - ac = ab + ac$.

De fleste elever vil formentlig i de første gennemløb af læringssporet synes, at et resultat som $ab+ac$ virker fremmedartet. De er vant til, at udtryk som $ab+ac$ udgør en beregning – og ikke resultatet af en beregning. Resultater har de oftest forbundet med talstørrelser. Ikke desto mindre udgør udtrykket selve resultatet i denne situation. Eleverne kan bruge tegningerne til at konstatere, at dette resultat rent faktisk udtrykker forskellen mellem antallet af sæder i den store og en af de små sale. Hvis de indsætter tal for $a$, $b$ og $c$, får de også mulighed for at se fordelen ved at udtrykke dette generelle resultat: Det gælder for alle de forskellige sale, der bliver delt på den beskrevne måde.

Som Albert antydede i eksemplet, kan forskellen mellem antallet af sæder i de to sale også udtrykkes på en anden måde: Det ene antal er dobbelt så stort som det andet. Sidst i læringssporet kan eleverne arbejde med sådanne multiplikative forskelle. Bogstavudtrykkene kan bruges til at vise denne forskel, idet $\frac{2ab+2ac}{ab+ac}=2$. Ved at bruge faktorisering og omskrivning af brøker får eleverne mulighed for at indse, at lighedstegnet gælder: $\frac{2ab+2ac}{ab+ac}=\frac{2(ab+ac)}{ab+ac}=2$.

Fasen kan udvides med aktiviteter, som giver eleverne mulighed for at få rutine med at bruge de regneregler, de arbejder med, samtidig med at de giver ’stof til eftertanke’. En sådan aktivitet kan fx være: