Praksis – At arbejde algebraisk
De tidsmæssige rammer
Læringssporet tænkes placeret i forlængelse af grundforløbet. Der kan arbejdes med det samlet, eller man kan opdele det i et forløb med fase 1 og 2 sammen og faserne 3 og 4 på et senere tidspunkt. Ved at behandle emnet selvstændigt som et samlet forløb sættes der fokus på de styrker, algebraen har fx i forbindelse med generaliseringer og ræsonnementer. Det kan øge elevernes opmærksomhed på faglige pointer, der kan henvises til i den efterfølgende undervisning, når man i konkrete tilfælde genbesøger disse pointer.
Klassens niveauvalg har betydning for, hvor stor vægt og hvor meget tid man vil bruge på faserne 3 og 4 med symbolmanipulation og bevisførelse. Sporet er tænkt til et forløb på 8-12 klokketimer, hvor de enkelte dele tages op i undervisningen igen under de efterfølgende emner.
Det faglige udgangspunkt
Ligningsløsningen i dette læringsspor bygger på elevernes erfaringer med ligninger, herunder løsningsmetoder fra grundskolen, hvor en ukendt størrelse, x, skal bestemmes. I afsnittet Oversigt ses de 4 forudsætninger, som læringssporet bygger på, og som kort udfoldes herunder.
Talmængder og regningsarterne: Eleverne har i udskolingen især arbejdet inden for de naturlige tal og de hele tal. Men i forbindelse med lineære funktioner har de også behandlet lineære ligninger. Her har de arbejdet inden for de rationale og de reelle tal – typisk dog uden at være klar over forskellen.
Eleverne har viden om regler for regning med reelle tal. De har udført beregninger i konkrete kontekster, der understøtter forståelsen af x som en ubekendt, der kan indgå i algebraiske udtryk og ligninger. De har også arbejdet med løsning af simple ligninger ved benyttelse af en række regneregler, der bringer x til at stå alene på den ene side i en ligning, mens resultatet står på den anden side. Det kan imidlertid ikke forventes, at alle elever har en grundlæggende forståelse for brug af algebra ved løsning af simple ligninger – og det gælder også, selvom de evt. kan løse sådanne ligninger.
Anvendelse at formler og algebraiske udtryk: Eleverne kan sætte tal i stedet for variable i en simpel formel, de kan anvende reelle tal og algebraiske udtryk i matematiske undersøgelser, og de kan sammenligne algebraiske udtryk.
Opstilling, omskrivning og beregning: Eleverne kan opdage og beskrive systemer i mønstre samt beskrive sammenhænge mellem enkle algebraiske udtryk og geometriske repræsentationer. Eleverne kan udføre omskrivninger og beregninger med variable.
Afsnittets indhold kan eksemplificeres med en opgave fra Folkeskolens prøver (december 2018, 9. klasse):
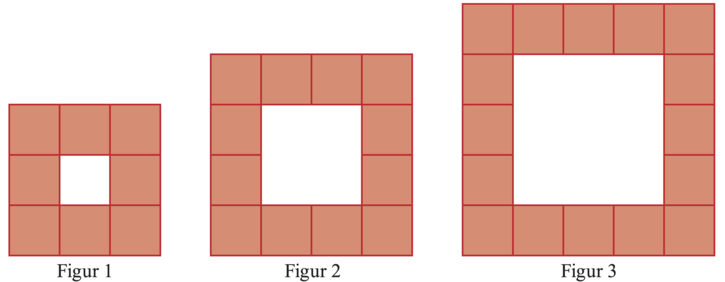
Eleverne skal opdage mønstret og bruge det til at tegne Figur 4. De skal bestemme, hvor mange kvadrater mønstret vokser med i hvert trin, og de skal vise, at et givet udtryk ikke beskriver mønstret. Eleverne skal ikke selv opstille men forklare, hvordan et givet udtryk er opstillet, og til slut sammenligner de to algebraiske udtryk ved omskrivninger.
Faserne
Afsnittet falder i to dele, hvor den kontekst eller model, som benyttes i arbejdet med algebra, er vidt forskellig. I første del benyttes en geometrisk model i form af prikmønstre og spiraltal, mens man i anden del anvender taltricks, dvs. talberegninger, som bagvedliggende model. Man kan naturligvis anvende andre gennemgående kontekster, fx funktioner givet i forskellige repræsentationer.
Kontekst 1: Figurfølger og talspiralen
Figurfølger kan fx bestå af figurer lavet af prikker, hvor antallet af prikker udvikler sig på en bestemt måde (se illustrationen i Oversigt). Spiraltal repræsenteres som en ”firkantet” spiral af $\mathbf{N}_0$. Man kigger fx på de tal, der står i hjørnerne af spiralen eller langs diagonalerne.
Fase 1
Med udgangspunkt i nedenstående figurfølge – et V-mønster, hvor antallet af prikker i hver figur er de ulige tal – bliver eleverne bedt om at formulere, hvordan mønsteret udvikler sig, og at indføre symboler og selv opstille et udtryk, der angiver udviklingen i antallet af prikker.

Nogle elever har brug for spørgsmål til at lede dem på vej. Man kan fx spørge: Hvor mange prikker er der i figurnummer 10? Eller i nummer 100? Hvordan kan man bruge et regneark til at bestemme disse tal?
Eleverne opdager mønstret $1, 3, 5, 7, \dotsc$, dvs. alle de ulige tal, og de kan beskrive det som fx, at der i hver figur tilføjes 2 prikker (aritmetisk generalisation). Fra forskningen ved man, at det kan hjælpe eleverne med at skabe mening i algebraiske udtryk, hvis man lader dem selv indføre de symboler, der skal bruges. Her kommer eleverne frem til udtrykket $2n -1$, hvor $n$ er figurnummeret. Mange elever vil nok benytte naiv generalisation, hvor udtrykket fremkommer som et (kvalificeret) gæt ud fra følgen af tal, der angiver antal prikker i hver figur og efterprøves på flere figurer. Men der kan være elever, som ud fra figuren kan komme frem til udtrykket gennem algebraisk generalisation ved at bemærke, at det ene ben i V’et har samme antal prikker som figurnummeret, og det andet ben har en prik mindre, så man får beregninger som $1$ og $2+1$ og $3+2$ osv., der generaliseres til $n + (n - 1) = 2n - 1$. Det er ikke en pointe her, at eleverne skal generalisere på en bestemt måde, men man kan sagtens allerede i denne fase begynde at italesætte, at der er flere måder at generalisere på og bruge gruppernes argumenter som illustration.
Der er til gengæld en pointe i, at eleverne erkender, at alle ulige tal kan beskrives som $2n-1$ (eller som $2n + 1$, hvis man vælger at kalde den første figur i figurserien for Figur nr. $0$ i stedet for Figur nr. $1$) – og senere at alle lige tal kan beskrives som $2n$, hvor $n$ er de hele tal.
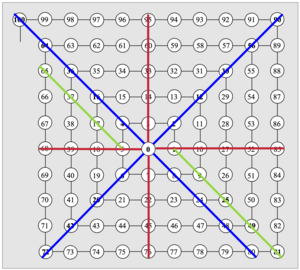
Efterfølgende kan der arbejdes med talspiralen. Den rummer udfordringer i forskellige grader, når det drejer sig om at opdage og beskrive talmønstre algebraisk.

Spiralen (se figuren ude til højre) har fire akser (røde) samt fire diagonaler (blå), der alle starter i tallet $0$. Tre af diagonalerne går gennem hjørnepunkter. Der er også linjer, som er parallelle med diagonalerne, men som starter et sted på en af akserne (grøn).
Man kan man finde mange regelmæssigheder langs disse akser, diagonaler og linjer i talspiralen – regelmæssigheder, som kan beskrives med ord og symbolske udtryk. Eleverne ledes på vej med spørgsmål som fx:
- Hvad lægger I mærke til, når I kigger på tallene i hjørnerne? Kan I beskrive tallene med et algebraisk udtryk?
- Bestem et udtryk, der giver tallene i diagonalen gennem tallene $0-4-16-\dotsc$ Brug dette resultat til at finde lignende udtryk for akserne og de andre diagonaler.
(Resultatet er $4n^2$, og går man i positiv omløbsretning til den første vandrette akse fås $4n^2+n$. Fortsæt i samme retning.)
Det kan være udfordrende at argumentere for udtrykkene ud fra talspiralen, men eleverne vil kunne komme frem til udtrykkene med naiv generalisering.
Fase 2
Når eleverne er blevet trygge ved at opdage, beskrive og indføre symboler i forbindelse med figurfølger og opstille algebraiske udtryk for disse, fortsættes med fase 2. Nu er udgangspunktet, at man har et algebraisk udtryk, der skal læses og fortolkes i en anden repræsentation – her en figurfølge – så det giver mening.

Man kan fx tage resultatet fra V-mønsteret op igen ved at give eleverne et udtryk som $1 + 3 + 5 + \dotsc + (2n - 1) = n^2$. Herefter de bliver bedt om at fortolke udtrykket i forhold til nedenstående figur (man kan evt. nøjes med at give dem figuren med V-mønsteret fra fase 1).
Eleverne kan komme frem til, at summen af de første n ulige tal er kvadratet på n. Måske er der elever, der allerede her bemærker, at forskellen mellem to på hinanden følgende kvadrattal altid er et ulige tal, så hver gang man lægger et nyt ulige tal til et kvadrattal, får man det næste. Det er indsigter som denne, der arbejdes med i fase 3.
Ud over at se på kvadrattallene kan man i denne fase introducere ”rektangeltal” og trekanttal.
Det algebraiske udtryk, der giver rektangeltallene, kan fortolkes ud fra mønstret vist herunder. Antallet af prikker i n’te figur, hvor den første figur består af 2 prikker, er det n’te rektangeltal, og det beregnes som $R_n = n(n + 1)$.

Eleverne får udtrykket og skal fortolke det som fx en figurfølge. Nogle grupper har brug for at se figurfølgen for at kunne læse mening ind i udtrykket, mens andre selv kan konstruere det. Der kan være elever, som udtrykker rektangeltallene på andre måder, fx sprogligt som ”ved at gange to fortløbende tal” eller som ”arealet af et rektangel, hvor den ene side er 1 større end den anden”. Nogle elever finder måske en alternativ algebraisk beskrivelse ud fra mønstret ved at se hver figur som et kvadrat med samme sidelængde som figurnummeret og dertil en ekstra søjle, så tallene kan bestemmes ved, $n^2 + n$. Alle disse fortolkninger tages op i en fælles klassediskussion.
Et rektangeltal er produktet af to fortløbende tal, fx $1 \cdot 2 = 2$ og $2 \cdot 3 = 6$ og $3 \cdot 4 = 12$ osv.
Et andet eksempel er trekanttallene, hvor antallet af kvadrater i hver figur af følgen er $T=\frac{n(n + 1)}{2}$. Igen skal eleverne læse mening ind i udtrykket ved at benytte en anden repræsentation, som her en figurfølge:

For at kunne fortolke udtrykket må eleverne udbygge mønsteret på fx denne måde:

Man kan anvende mange andre algebraiske udtryk, der kan fortolkes i forskellige repræsentationer. Ved at lade eleverne møde symbolerne i forskellige repræsentationsformer giver man dem en bedre mulighed for at skabe mening i de algebraiske udtryk.
Nogle elever kan arbejde videre med kvadrattallene i talspiralen og fortolke udtrykket $1 + 3 + 5 + \dotsb + (2n-1) = n^2$ som en måde at beregne tallene i den diagonal, der går gennem hjørnepunkterne. Her kan eleverne bruge resultatet fra V-mønsteret; nemlig at værdien af stigningen fra ét kvadrattal til det næste er 2 pga. spiralens struktur, der i hver halve runde vokser med 2 (fra 1 til 4 er der 3, fra 4 til 9 er der 5 osv.).

Fase 3
I denne fase går man videre fra symbolisering og opstilling af udtryk samt at læse mening ind i dem til at undersøge og ræsonnere om og med de opstillede algebraiske udtryk. Hermed kommer man et skridt videre med henblik på at udvikle objektforståelse.
Fra fase 1 og 2 kender eleverne de algebraiske udtryk for kvadrattallene, rektangeltallene og trekanttallene. I fase 3 skal disse tal undersøges nærmere med henblik på at opdage nye sammenhænge og opleve algebraens styrker til beskrivelse af sådanne sammenhænge.
Som et eksempel på en undersøgelse, der ligger i direkte forlængelse af dem, eleverne har lavet i de tidligere faser, kan man fx bede dem finde ud af, hvad man får, når man lægger de første $n$ lige tal sammen; $ 2 + 4 + 6 + 8 + \dotsb$ op til $n$. Denne gang får de ingen mønstre, men bliver i stedet opfordret til at anvende de metoder og resultater, de er kommet frem til tidligere.
Nogle elever vil argumentere ud fra talrækken. De kender summen af de første $n$ ulige tal, der er $n^2$. Så hvis de lægger $1$ til hvert ulige tal, må det give summen af de første $n$ lige tal. Men så skal der også lægges $n$ til på højresiden af udtrykket, hvilket fører frem til $2 + 4 + 6 + 8 + \dotsb + 2n = n^2 + n$. Måske genkendes dette som $n(n + 1)$, der er rektangeltallene.
Selvom tanken er, at eleverne i denne fase primært skal arbejde med de algebraiske udtryk, vil nogle grupper have brug for at støtte sig til mønstre og argumentere ud fra disse. Eleverne har måske bemærket at man i mønstret for rektangeltallene netop fik den næste figur i rækken ved at lægge det næste lige tal til, helt parallelt til det de gjorde med kvadrattallene i V-mønstret. De kan forklare summen ud fra mønstret for rektangeltallene, der viser, at summen af de første $n$ lige tal kan skrives som $2 + 4 + 6 + 8 + \dotsb + 2n$, der kan udtrykkes som $n(n + 1)$.
Som en fortsættelse kan man bede eleverne bruge resultatet til at finde summen af de første $n$ tal. Hvis man dividerer det algebraiske udtryk for summen af de $n$ lige tal med $2$, giver det $1 + 2 + 3 + \dotsb + n = \frac{n(n + 1)}{2}$, som jo netop er trekanttallene! På denne måde kan eleverne opnå yderligere indsigt i forbindelsen mellem de algebraiske udtryk indbyrdes og sammenhængen med deres andre repræsentationer.
I en fælles klassediskussion, hvor elevernes resultater og argumenter tages op, kan man bemærke forskelle og ligheder på, hvordan grupperne ræsonnerer og generaliserer, og hvordan man kan komme frem til de forskellige udtryk på flere måder.
Dygtige elever kan se på spiraltallene og arbejde videre med de udtryk, der blev fundet for akser og diagonaler i fase 1, fx kan de selv forsøge at argumentere for, hvilke udtryk der giver tallene langs de linjer, der er parallelle med diagonalerne.

Fase 4
I fjerde og sidste fase af læringssporet formaliseres arbejdet med at ræsonnere om og med algebraiske udtryk til egentlig bevisførelse. I dette læringsspor lægges der udelukkende op til direkte bevisførelse ved at omskrive algebraiske udtryk. Gennem en følge af ækvivalente ligninger kan eleverne vise matematiske påstande, som enten er givet, eller som de selv formulerer, fx på baggrund af mønstre og talspiralen. Man kan begynde med at give eleverne nogle påstande, der skal bevises algebraisk, fx:
Påstand 1: Produktet af to rektangeltal er igen et rektangeltal.
eller
Påstand 2: Hvis man ganger et vilkårligt rektangeltal med 4 og lægger 1 til, får man altid et kvadrattal.
Figuren viser en geometrisk fortolkning af påstanden, men I skal vise den algebraisk!
Man kan også bede eleverne om selv at formulere en påstand, fx:
Prøv at lægge to på hinanden følgende trekanttal sammen. Hvad ser I? Formuler en påstand, og vis den ved beregning.
Nogle elever vil have glæde af at se den søgte påstand visuelt.
Dygtige elever kan selv finde gentagelser og sammenhænge i talspiralen, mens andre har brug for, at man henleder deres opmærksomhed på sådanne. Det kan fx være sammenhænge som disse:
I talspiralen kan man observere, at alle kvadrattal ligger på samme måde i forhold til to fortløbende rektangeltal (observation: Kvadrattallene ligger lige midt imellem to fortløbende trekanttal). Formuler en påstand ud fra denne observation, og bevis den (bevis: $n^2$ ligger midt imellem $n(n -1) = n^2 - n$ og $n(n + 1) = n^2 + n$).
I fase 3 var der måske elever, der fandt frem til udtryk for tallene, der ligger på linjer parallelt med diagonalerne. Disse udtryk kan nu give anledning til at formulere og vise en påstand ud fra følgende observation:
I talspiralen ser det ud til, at alle tallene langs en af de rette linjer, der er parallelle med diagonalerne, er enten lige eller ulige. Formuler en påstand ud fra denne observation og bevis den.
Kontekst 2: Taltricks
Et taltrick er en række beregninger med udgangspunkt i et tal, eleven selv vælger, som fører til et på forhånd givet resultat. Tricket består i at opdage og beskrive, hvordan beregningerne altid fører til dette resultat uafhængigt af det tal, man starter med.


Fase 1
Undervisningen indledes med et taltrick, der fx indeholder nogle beregninger, som eleverne er vant til at udføre. Det kan fx se ud som nedenstående, hvor alle elever ender med det samme tal som det, de havde valgt. Man kan også bruge et taltrick, hvor alle ender med det samme tal.

Eleverne skal derefter finde frem til ”tricket”. Hvorfor får man det tal, man startede med? Nogle elever vil have glæde af at skrive de konkrete beregninger ned for flere valgte tal, evt. i mindre grupper. Andre elever vil straks indføre et symbol for det valgte tal og opskrive en generaliseret beregning som bogstavudtryk. Et skema som nedenstående kan hjælpe dem i processen fra tal til bogstaver.
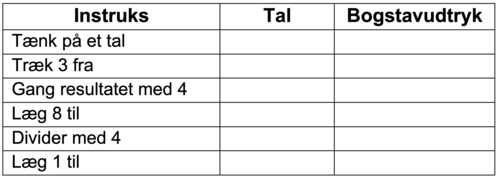
For alle elever er målet, at de selv skal indføre et symbol for det tal, de vælger, og ud fra de givne instrukser opstille et generelt udtryk for den sammenhæng, der fører fra det valgte tal til det på forhånd givne resultat. Herefter skal udtrykket omformes vha. grundlæggende regneregler, så det bliver klart, at man ender med det ønskede resultat. Man kan bruge flere taltricks og designe dem, så eleverne får behov for at bruge forskellige grundlæggende regneregler. Elever, der hurtigt fanger den bagvedliggende matematik, kan designe deres egne taltricks, som fx skal indeholde brugen af en bestemt regneregel, eller som skal føre til et bestemt tal. I den opsamlende klassediskussion kan grupperne sammenligne deres udtryk, så de oplever, at omformningerne kan foretages på forskellig måde, og at der er flere veje at gå.
Fase 2
Når eleverne har fået erfaringer med at gennemskue de forholdsvis simple taltricks i fase 1, kan man gå videre med lidt mere udfordrende taltricks. Her vises et eksempel på et taltrick, der fører til 1. kvadratsætning. Hvis man allerede har arbejdet med kvadratsætningerne, må man finde et andet udgangspunkt.
Da pointen i denne fase er at læse og fortolke algebraiske udtryk, kan man vælge at give eleverne et allerede delvist udfyldt skema som nedenstående. Her er beregningerne vist, og man kan enten opskrive de tilhørende bogstavudtryk i fællesskab i klassen eller på forhånd have udfyldt den tredje søjle, så skemaet er helt udfyldt.

Efter eleverne har fulgt instrukserne og sammenholdt dem med beregninger og bogstavudtryk, tegnes nedenstående figur på tavlen. Elevernes opgave består nu i at fortolke de beregninger og udtryk, som de lige har arbejdet med i forhold til figuren. Hvilke arealer har de fundet? Og hvorfor ender man med et areal på $0$?

Efterfølgende kan eleverne fx arbejde med lignende problemstillinger, der giver dem mulighed for at læse og fortolke algebraiske udtryk i en kontekst (her beskrevet ved arealer). Skemaet herunder viser et taltrick, der fører til 2. kvadratsætning, $(a- b)^2 = a^2 + b^2 - 2ab$, og som eleverne kan fortolke ved selv at lave en figur af samme type som ovenfor, der kan forklare sammenhængen mellem arealet $a^2 + b ^2 - 2ab$ og arealet $(a - b)^2$.

Igen kan man selv finde mange flere sammenhænge, der understøtter, at eleverne kan læse og fortolke algebraiske udtryk.
Fase 3
I denne fase, hvor eleverne skal undersøge algebraiske udtryk, benyttes taltricks som stilladsering for at lede eleverne mod en bestemt indsigt. Nedenstående taltrick er designet til at få eleverne til at opdage, hvordan et flercifret tal kan skrives op ud fra de givne cifre:

Når eleverne har indset, at det flercifrede tal $abc$ kan skrives som $a \cdot 100 + b \cdot 10 + c$, kan de bruge deres viden til at undersøge og argumentere for resultatet af nedenstående taltrick: Hvorfor får alle elever et tal, der ligger i 9-tabellen?

Gennem et taltrick som dette opnår eleverne en indsigt i, hvordan man kan ræsonnere med algebraiske udtryk.
Også her er det en god idé at gentage aktiviteten med andre enkle taltricks for at konsolidere elevernes forståelse af og erfaring med den formelle måde at opskrive flercifrede tal på.
Fase 4
I denne fase bygges der videre på de indsigter og erfaringer, eleverne fik i fase 3. Men hvor man i de tidligere faser har afsluttet hvert taltrick med en opsamling af elevernes resultater, fx at alle får det samme tal, eller at alle tal er deleligt med 9, bliver eleverne nu bedt om selv at formulere en påstand om, hvad taltricket viser. Nedenfor ses et taltrick, der fører til påstanden: For ethvert tocifret tal, der ender på 5, vil kvadratet på tallet ende på 25, og foran 25 står produktet af første ciffer og det tal, der er 1 større.

Det kan være nødvendigt at lade eleverne afprøve taltricket med flere tal, før de kan få formuleret en påstand. En struktureret opskrivning af hele klassens resultater på tavlen kan også danne udgangspunkt for elevernes formuleringer.
Herefter arbejder eleverne i grupper med at bevise påstanden ved hjælp af opskrivningen af deres valgte tal som fx $a \cdot 10 + 5$.
Det videre arbejde
En stor del af matematikken i gymnasiet hviler på algebra i større eller mindre udstrækning. Det er derfor oplagt at tage de metoder og resultater, som eleverne er kommet frem til i dette læringsspor, op igen, hvor det er naturligt at minde dem om, hvad de kom frem til her, og hvordan det bruges i nye sammenhænge n– fx når man indfører symboler, opstiller funktionsudtryk og bruger dem i problemløsning, eller når man viser sætninger om funktioners opførsel. Det er også vigtigt ”at gå den anden vej” og lade elever læse og fortolke funktionsudtryk, så de kan give mening i fx en given kontekst. Andre fag vil forvente, at eleverne er i stand til at udføre symbolmanipulationer og anvende symbolske udtryk, så det er vigtigt, at eleverne får erfaringer med dette i matematik.