Tilgang – At addere brøker

Afsnittet beskriver de vigtigste faglige idéer i læringssporets fire faser (se oversigten).

Når der begyndes på at arbejde med egentlig brøkregning som addition, er det vigtigt, at klassen har opbygget en grundlæggende forståelse af brøkbegrebet. Det vil sige, at det faglige udgangspunkt er, at eleverne har opbygget en god forståelse af, hvilken værdi en brøk angiver; fx ved at kunne placere brøker på en tallinje. Det er centralt, at eleverne således er begyndt at integrere brøker i deres talbegreb. Naturligvis udvikler elevernes forståelse af brøkbegrebet sig også gennem arbejdet med addition, men forståelsen af, hvilke værdier brøksymboler repræsenterer, skal være forholdsvis sikker, inden der arbejdes med at udvikle en metode til brøkaddition.

Grundlæggende sker der to sideløbende bevægelser i læringssporet. Den ene bevægelse er, at eleverne gradvist udvikler deres forståelse af at addere to brøker. I denne bevægelse skal klassen samtidig blive opmærksom på, hvordan brøker er anderledes at addere end de naturlige tal (se Tabel 1). I bevægelsen sker der en progression i det matematiske indhold gående fra addition med ens nævner, addition, hvor den ene brøk skal omskrives for at finde en fælles nævner, og til slut addition, hvor begge brøker skal omskrives for at finde fællesnævneren. Den anden bevægelse går fra et afsæt i at bruge konkrete materialer, som oversættes til brøksymbolet, til et afsæt, hvor brøksymbolet oversættes til konkrete materialer, tegninger og hverdagssprog – og på sigt kan klassen slippe brugen af konkrete materialer helt. Det at slippe de konkrete materialer helt er dog en proces, der tager tid. Nogle udskolingselever vil stadig have behov for at repræsentere regnestykker med brøker gennem tegninger.

I læringssporet skal klassen blive opmærksom på forskellene mellem at lægge naturlige tal og brøker sammen. Der er to primære forskelle, som eleverne skal erfare, når de går fra arbejdet med addition inden for de naturlige tal til at arbejde med addition med brøker:

Den første forskel mellem de naturlige tal og brøker, som eleverne oplever, når de skal addere to brøker, er, at nævnerne ikke skal lægges sammen; det er kun tællerne, der skal lægges sammen. Denne forskel opleves ofte som værende årsag til den gennemgående fejl, mange elever laver – nemlig, at de også lægger nævnerne sammen, fx $\frac{1}{3}+\frac{1}{4}=\frac{2}{7}$. Årsagen til fejlen kan være, at undervisningen fokuserer på at lære klassen at bruge en metode trin for trin uden samtidig at have fokus på at opbygge forståelse for metoden eller på at støtte elevernes udvikling af brøkbegrebet. Denne fejl kan være funderet i en heltalsdistraktor, idet eleverne betragter en brøk som bestående af to separate tal over og under en streg, som ikke indgår i nogen relation eller forhold med hinanden. 

Den anden forskel, klassen skal erfare, når de arbejder med addition af brøker, er, at der er uendeligt mange additionsstykker, som giver samme resultat (resultatet kan derudover skrives på uendeligt mange måder). Også af den grund vil det ikke give mening at forsøge at huske resultater af additioner af brøker, fx $\frac{1}{3}+\frac{3}{4}=\frac{13}{12}$. Med andre ord er der inden for de naturlige tal et endeligt antal af to addender, der giver et bestemt resultat. Fx kan $3$ fås ved $1 + 1 + 1$ eller $2 + 1$ eller $3 + 0$. Inden for brøker er der imidlertid et uendeligt antal af to addender, der giver et bestemt tal, fx $3$. Hvis klassen tidligere har arbejdet med negative tal, har de muligvis erfaret, at der er uendeligt mange addender, der kan give et bestemt resultat. Forskning viser, at eleverne skal have opbygget en forståelse af brøkers værdi for at kunne arbejde med regneoperationerne inden for brøker; fx at kunne anslå, om en given brøk er over eller under $\frac{1}{2}$ eller tæt på 1. Det giver eleverne mulighed for at kunne vurdere og forstå værdien af de brøker, de arbejder med. Når eleverne fx skal addere $\frac{1}{12}$ og $\frac{7}{8}$, skal de have en fornemmelse af, at summen må være tæt på $1$ – altså en talforståelse. Det kan ses gennem ræsonnementet: $\frac{1}{12}$ er tæt på $0$, mens $\frac{7}{8}$ er tæt på $1$, så summen må være tæt på $1$. 

Det er centralt, at klassen fleksibelt kan anvende forskellige repræsentationer af brøker (tallinjen, cirkeldiagrammer, brøkbrikker osv.), da repræsentationerne kan støtte deres ræsonnementer, når de arbejder med at addere to brøker. Dog er det ikke hensigtsmæssigt at repræsentere brøker som 'et antal ud af en mængde', når der skal adderes eller subtraheres, dvs. at betragte $\frac{1}{4}$ som en rød centicube ud af fire og $\frac{2}{5}$ som to røde centicubes ud af fem. Når disse brøker adderes med afsæt i denne repræsentation, risikerer den følgende fejl at opstå hos eleverne: de ser det som to mængder af naturlige tal, der adderes. Den ene røde centicube plus de to røde centicubes, og de fire røde centicubes plus de fem røde centicubes, hvilket er tre røde centicubes ud af ni ($\frac{3}{9}$).

Mange elever starter med at arbejde med additions- eller subtraktionsstykker, uden at eleverne har et billede af de værdier, brøkerne repræsenterer. En tommelfingerregel er, at eleverne ikke skal starte på at arbejde med de standardiserede regnemetoder til addition eller subtraktion, før de har en intuitiv tilgang til at kunne løse stykker á la dem i Tabel 2.

Betydningen af nævnerne spiller en nøglerolle i strategier inden for brøkaddition, fordi valg af strategi i høj grad afhænger af forholdet mellem de to nævnere. Nævnernes forhold er afgørende for, om der skal findes en fællesnævner, og hvilken fællesnævner det er smart at bruge. At addere to brøker kan ses som en proces med fire trin:

• Trin 1: Find fællesnævneren af de to brøker. (Hvis de har fællesnævner springes til trin 3 fx $\frac{2}{3}+\frac{1}{3}$). 

• Trin 2: Forlæng begge brøker, så de får en fællesnævner.

• Trin 3: Addér tællerne og brug fællesnævneren.

• Trin 4: Se om summen af de to brøker kan forkortes eller omskrives til blandede tal. (Det skal dog vurderes, om det giver mening i forhold til konteksten af opgaven. Det giver ikke altid mening at omskrive eller forkorte).

Særligt trin 1 og 2 kræver, at eleverne kan veksle mellem forskellige strategier.

• Strategi 1: Ens nævner
  Denne strategi anvendes på stykker, hvor de to addender har samme nævner – her adderes tællerne. Fx $\frac{1}{7}+\frac{1}{7}=\frac{2}{7}$.
• Strategi 2: Omskriv den ene brøk
  Denne strategi anvendes på stykker, hvor det kun er nødvendigt at omskrive den ene brøk for at få en fællesnævner, inden tællerne kan lægges sammen. Fx $\frac{1}{6}+\frac{1}{3}=\frac{1}{6}+\frac{2}{6}$.
  Her anvendes naturligt tidligere strategier knyttet til addition med etcifrede tal. Se evt. læringssporet At forstå brøker.
• Strategi 3: Omskriv begge brøker ved at multiplicere nævnerne
  Denne strategi anvendes på stykker, hvor det er nødvendigt at omskrive begge brøker for at få en fællesnævner, inden tællerne kan lægges sammen. Fx $\frac{3}{5}+\frac{1}{4}$.
  Den mindste fællesnævner findes i dette tilfælde ved at multiplicere de to nævnere med hinanden – altså $5 \cdot 4 = 20$ – og forlænge hver af brøkerne – altså $\frac{3}{5}+\frac{1}{4}=\frac{3 \cdot 4}{5 \cdot 4}+\frac{1 \cdot 5}{4 \cdot 5}=\frac{12}{20}+\frac{5}{20}$. Det er også den generelle metode, som altid vil virke, når to brøker skal adderes.
• Strategi 4: Omskriv begge brøker ved at finde mindste fælles multiplum
  Denne strategi kræver en god forståelse af multiplikation, idet den mindste fællesnævner også kan findes ved at finde mindste fælles multiplum af de to nævnere. Fx er $24$ ikke mindste fællesnævner for $\frac{1}{4}+\frac{1}{6}$; det er $12$, altså $\frac{1}{4}+\frac{1}{6} = \frac{1 \cdot 3}{4 \cdot 3}+\frac{1 \cdot 2}{6 \cdot 2}=\frac{3}{12}+\frac{2}{12}$. Det vil være ganske få elever, der vil kunne bruge primtalsfaktorisering som en måde at finde den mindste fællesnævner, men elever vil kunne trække på deres viden om tabeller og bruge den til at finde de forskellige tals multipla. Fx er de positive multipla af $6$ mængden $\{6, 12, 18, 24, 30, ...\}$, mens de positive multipla af $4$ er $\{4, 8, 12, 16, 20, 24, ...\}$. Her kan man se, at $12$ og $24$ er fælles multipla for de to tal – de er i begge mængder eller tabeller.
• Opsamling
  Overordnet er processen med at forstå og finde fællesnævner det centrale. Det kompliceres af, at eleverne er nødt til at forholde sig samtidigt både til brøkerne, fx i $\frac{3}{5}+\frac{1}{4}$, og den underliggende helhed. Den underliggende helhed er den, der gør, at $\frac{3}{5}$ og $\frac{1}{4}$ er taget af den samme størrelse. Fx kan $\frac{3}{5}$ familiepizza ikke adderes med $\frac{1}{4}$ børnepizza.
  Når eleverne har adderet to brøker ved brug af en af disse strategier, skal de forholde sig til, om brøken kan forkortes eller evt. omskrives til et blandet tal. Det skal understreges, at ovenstående ikke er en fyldestgørende liste over strategier. En anden oplagt strategi er at omskrive brøker til decimaltal, men dette vil ikke blive berørt i dette læringsspor.

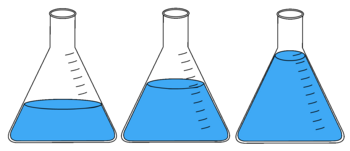
I fase 1 arbejder klassen med den overordnede forståelse af at anslå, hvad summen af to brøker kan være. Det er vigtigt, at eleverne får en fornemmelse af, hvilken værdi hver af de to addender repræsenterer for derigennem at kunne vurdere, om summen er tæt på $0$, $\frac{1}{2}$ eller over $1$. Klassen arbejder således med uformelle tilgange til at addere brøker og anslå deres sum gennem brug af konkrete materialer, som fx fyldte glas (se Figur 1). At anslå en sum kræver, at eleverne har udviklet en grundlæggende forståelse af brøker, som gør dem i stand til at ræsonnere uformelt over, hvor stor summen af to brøker er. Der tages afsæt i at måle og bruge konkrete materialer.

I fase 2 skal klassen erfare betydningen af nævneren og tælleren ved addition. Fasen bygger videre på den uformelle tilgang til addition med brøker i fase 1, men nu arbejder klassen videre med at finde det nøjagtige resultat. Der er derfor et særligt fokus på additionsstykker, hvor nævnerne er ens, for at reducere kompleksiteten. Det vil sige, at eleverne arbejder primært på det første trin inden processen med at addere to brøker; altså strategien ens nævner.

Det er centralt, at eleverne kan anslå eller forstille sig værdien af de brøker, de arbejder med, og på den måde overføre deres viden om addition inden for de naturlige tal til brøkerne – nemlig at summen af to addender bliver større. Når nævnerne er ens, gøres dette arbejde lettere, da de kun skal forholde sig til én nævner. Det har også vist sig, at eleverne laver færre fejl i additionsstykker, når nævnerne er ens, hvilket indikerer, at eleverne har en større forståelse af additionen, da de undgår udfordringen med at finde en fællesnævner.

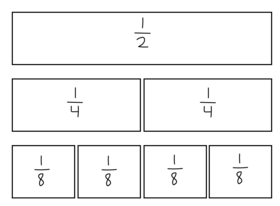
Desuden arbejdes med, at klassen erfarer, at der er uendeligt mange additionsstykker, der kan give en bestemt sum. Som tidligere nævnt er der uendeligt mange stykker inden for addition med brøker, der kan give en bestemt sum, idet addenderne kan forlænges med det samme tal, uden at deres værdi ændres. Fx kan summen $\frac{1}{2}$ fås ved $\frac{1}{4} + \frac{1}{4}, \frac{2}{8} + \frac{2}{8}, \cdots, \frac{100}{400} + \frac{100}{400}, \cdots$ (se Figur 2). Dette er med til at støtte eleverne i, at der er mange mulige valg af fællesnævnere. En anden måde at få summen $\frac{1}{2}$ er ved at gøre den ene brøk større og den anden tilsvarende mindre, fx $\frac{3}{8}+\frac{1}{8}$ og $\frac{199}{400}+\frac{1}{400}$. Ved at arbejde med forskellige måder at få summen $\frac{1}{2}$ kan eleverne udvikle ny forståelse af tætheden inden for de rationale tal. Det kan støtte eleverne i ikke at bruge en hukommelsesstrategi inden for brøker, da de ikke vil være i stand til at huske summerne af alle addenderne.

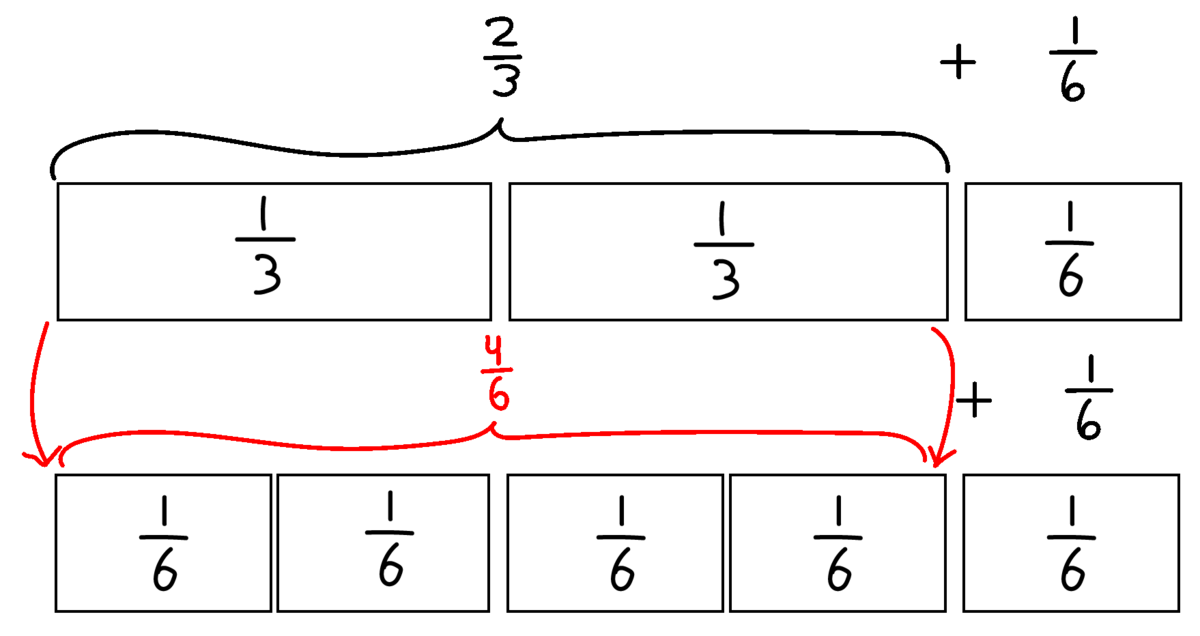
Fase 3 skal ligge i umiddelbar forlængelse af fase 2. I denne fase er der fokus på at støtte klassens begyndende forståelse af fællesnævner og at opbygge fleksible strategier til addition af brøker. Eleverne skal støttes i at fokusere på nævnerens betydning for, hvilken strategi der er hensigtsmæssig at vælge. I fasen arbejder klassen med at forstå nødvendigheden af at forlænge den ene addend for at skabe en fællesnævner, og fokus er derfor på strategien Omskriv den ene brøk. I $\frac{2}{3}+\frac{1}{6}$ er det fx smart at forlænge $\frac{2}{3}$ til $\frac{4}{6}$, da brøkerne kan adderes: $\frac{4}{6}+\frac{1}{6}$. Arbejdet med at forlænge den ene brøk bør ske med støtte i konkrete materialer. Klassen kan fx bruge brøkbrikker, hvor summen af de to brøker vises ved at lægge brøkbrikkerne efter hinanden og undersøge, hvordan den viste sum kan beskrives, fx som $\frac{5}{6}$ (se Figur 3). Hvis eleverne har vanskeligt ved at forstå, hvorfor $\frac{2}{3}$ er ækvivalent med $\frac{4}{6}$, bør læreren gå til det tidligere læringsspor ’At forstå brøker’. Igen kan det være en idé at tale om, at eleverne også kan finde andre fællesnævnere; bl.a. ved at forlænge dem, så stykket overfor fx bliver $\frac{8}{12}+\frac{2}{12}$.

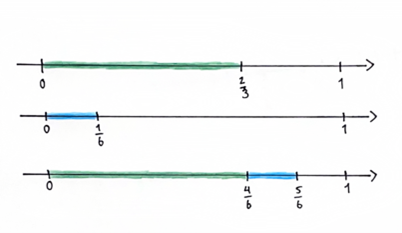
I fasen skal eleverne desuden sættes i situationer, hvor de skal argumentere for, at fx $\frac{2}{3}+\frac{1}{6}=\frac{3}{9}$ ikke er korrekt. Det kan gøres ved, at eleverne forholder sig til de værdier, brøkerne repræsenterer, og kommer med et overslag på, hvad summen af additionen cirka giver, så der opstår en kognitiv konflikt imellem deres estimering og resultatet af udregningen. Det kan gøres gennem tegninger eller konkrete materialer, som stadig bør inddrages aktivt i denne fase. Eleverne kan fx placere de to brøker på hver sin tallinje og bagefter lægge de to længder efter hinanden på en ny tallinje (se Figur 4). Det centrale er, at eleverne forholder sig til, om summen af de to brøker kan anslås til at være fx under en halv eller omkring 1.

I slutningen af denne fase bør klassen møde additionsstykker, hvor en fællesnævner også kan findes ved at forkorte den ene addend. Det kan fx være $\frac{3}{12}+\frac{1}{4}$, som både kan løses ved at forlænge $\frac{1}{4}$ til $\frac{3}{12}$, men også ved at forkorte $\frac{3}{12}$ til $\frac{1}{4}$. Ligesom med regnestrategierne inden for de naturlige tal er det centralt, at eleverne forholder sig til de tal, som indgår i regnestykket, så de kan finde en god og smart måde at løse stykket på.

I fase 4 arbejder klassen med additionsstykker, hvor eleverne har brug for at forlænge begge brøker for at finde en fællesnævner, fx $\frac{1}{3} + \frac{1}{4}$. Det vil sige, at klassen arbejder videre med deres erfaringer fra fase 3 om at finde den nøjagtige sum af to brøker, men nu er der behov for at forlænge begge addender. Igen skaber klassen deres nye erfaringer gennem brug af konkrete materialer, der kan anskueliggøre den størrelse, de skal finde den nøjagtige værdi af. I fasen arbejdes fortsat med, at eleverne udvikler fornemmelser for brøkers værdier.

I fasen arbejdes med strategier til at finde en fællesnævner for brøkerne. Den ene strategi, Omskriv begge brøker ved at finde mindste multiplum, er at ’gå på jagt’ efter mindste fælles multiplum ved at tænke i tabeller. Den anden strategi, Omskriv begge brøker ved at multiplicere nævnerne, er at forlænge hver brøk med den anden brøks nævner. Vær opmærksom på, at det centrale i arbejdet er elevernes forståelse af tallene og strategierne. Det kan derfor være en fordel ikke bare at vise strategierne og lade eleverne bruge dem pr. automatik. En mulighed er at inddrage eleverne i problemet med at finde ’gode fællesnævnere’, lade dem gå undersøgende til værks og give dem mulighed for at ’genopdage’ regneregler, der kan gælde i forskellige situationer.