Praksis – At addere brøker
I denne del af teksten udfoldes læringssporet med henblik på brug i undervisning. Først omtales de tidsmæssige rammer, som sporet er tænkt indenfor. Derefter beskrives den viden og kunnen hos eleverne, som sporet bygger videre på. Til sidst uddybes hver af de fire faser, som læringssporet består af.
De tidsmæssige rammer
Det vil ofte være passende at begynde læringssporet i slutningen af 4. klasse eller begyndelse af 5. klasse. Det centrale er, at klassen har opbygget en god forståelse af brøker, inden de meningsfuldt kan addere brøker med hinanden. Naturligvis udvikler eleverne også deres talforståelse af brøker ved at arbejde med addition – men hvis de ikke har opbygget en forståelse af, hvilke værdier, forskellige brøker repræsenterer, vil arbejdet med addition hurtigt blive til automatiserede metoder uden forståelse af regneoperationen. I de fleste klasser vil det være hensigtsmæssigt at lade læringssporet strække sig over et forløb af ca. 3 ugers varighed.
Det faglige udgangspunkt
Forståelse af brøker bygger videre på elevers tidligere erfaringer med brøker og de naturlige tal. Det er naturligvis vigtigt, at der skabes et sammenhængende talbegreb, hvor addition med brøker kan udvide elevernes forståelse af beregninger med tal, så den overordnede forståelse af addition bliver udbygget. Selvom de naturlige tal kan distrahere eleverne i deres forståelse af addition med brøker i form af heltalsdistraktorer, er forståelsen af de naturlige tal også central, når det gælder regneoperationer med brøker. Det er derfor centralt, at eleverne har et godt fagligt udgangspunkt, som er vist i Oversigten.
Den første forudsætning er, at eleverne har en grundlæggende forståelse af, hvilken værdi en brøk repræsenterer. Eleverne kan vise det ved, at de kan angive, om en brøk er tæt på størrelserne $1$ eller $\frac{1}{2}$ eller $0$.
For det andet er det en forudsætning, at forståelsen af ækvivalente brøker er udbygget og sikker, så eleverne både kan forlænge og forkorte brøker samt forstå, at forskellige brøker kan repræsentere den samme størrelse. Det kan være vanskeligt, når vores termer 'forkorte' og 'forlænge' kan indikere, at brøkerne bliver kortere eller længere.
For det tredje er det en forudsætning, at eleverne kan addere og multiplicere etcifrede, naturlige tal og er sikre i deres forståelse af regnearterne inden for de naturlige tal. Det betyder, at eleverne skal have en forståelse af fx den kommutative lov ($a \cdot b = b \cdot a$) – at resultatet af $4 \cdot 3$ er det samme som $3 \cdot 4$. Overordnet skal eleverne altså have opbygget en forståelse for multiplikativ tænkning som noget andet end additiv tænkning. Multiplikativ tænkning vedrører at kunne genkende og løse problemer, der involverer multiplikation og division som fx problemer af typen ’Hvor mange gange større er $a$ end $b$? Elever, der er langt i deres multiplikative tænkning ved fx, at $6$ er tre gange større end $2$, og at $12$ er tre gange større end $4$. De har derfor et grundlag for at forstå, at $\frac{2}{6}$ er udtryk for samme størrelse som $\frac{4}{12}$.
Den sidste og fjerde forudsætning er, at eleverne kan omskrive uægte brøker til blandede tal; altså $\frac{5}{3} = 1 \frac{2}{3}$. Der bliver ikke i sporet fokuseret på denne omskrivning, men den vil naturligt blive inddraget, når summen af additionen vurderes: Kan vi forkorte resultatet? Hvor mange hele får vi?
Multiplikativ tænkning kommer fx til udtryk i forståelse af, at forholdet mellem tæller og nævner er konstant i ækvivalente brøker. Det vil sige, at $\frac{1}{3}$ og $\frac{2}{6}$ repræsenterer samme størrelse, fordi $1$ til $3$ er det samme forhold som $2$ til $6$.
Med en additiv tænkning kan man tro, at $\frac{2}{3}$ og $\frac{3}{4}$ er den samme størrelse, da der er $1$ i forskel mellem tæller og nævner; altså $3-2$ og $4-3$.
Fase 1
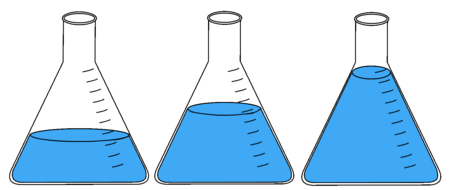
Fasen strækker sig over en til to lektioner. En aktivitet kan fx tage udgangspunkt i tre store glas med saftevand på kateteret. Det ene glas er $\frac{1}{2}$ fyldt, det andet er $\frac{1}{3}$ fyldt, og det sidste er $\frac{1}{6}$ fyldt.
Fase 1
At give overslag på resultatet af addition af brøker med støtte i konkrete materialer.
Glas med saftevand
Først skal eleverne parvis diskutere, hvor meget saftevand der er i de enkelte glas. Læreren samler derefter op på tavlen ved at tegne de tre glas og skrive gruppernes bud på, hvilken brøk der betegner, hvor meget saftevand der i glassene på tavlen. Gennem klassesamtalen bliver klassen enig om, hvor stor en del af glasset der er fyldt. Mål gerne efter, så klassen bliver enig om, at glassene er nøjagtigt fyldt $\frac{1}{2}$, $\frac{1}{3}$ og $\frac{1}{6}$. Hvis eleverne virker usikre på, hvordan man beskriver de fyldte glas med brøker, skal der arbejdes med at forstå brøkbetegnelse, og man skal vende tilbage til det tidligere læringsspor om At forstå brøker.
Herefter bliver eleverne bedt om at komme med bud på, hvor meget glasset vil blive fyldt, hvis vi hælder glasset $\frac{1}{3}$ og $\frac{1}{2}$ sammen i et glas. Og til slut diskuteres det, om glasset løber over, hvis vi fylder det sidste glas med $\frac{1}{6}$ oveni (se Figur 5).
Eleverne kan arbejde videre med additionsstykker, hvor der er tegnet forskellige glas, der skal fyldes og lægges sammen, og vurdere, hvornår glasset vil løbe over.
Arbejdet med at anslå størrelsen af summen af to brøker bør fortsætte gennem arbejdet med tallinjen. Først indtegnes de tre brøker på hver sin tallinje. Herefter samles de tre brøker i en tallinje under, så længden af de tre brøker ligger efter hinanden. Eleverne aflæser slutpunktet på tallinjen (se Figur 6). Herefter fortsætter eleverne med at arbejde inden for andre repræsentationer, fx cirkeldiagrammer.

Fase 2
Fase 2 kan fx strække sig over to lektioner. Afsættet er i konkrete materialer til at anskueliggøre additionsopgaven. Disse kan være i form af brøkbrikker eller papbrikker, eleverne selv har fabrikeret.
I denne fase arbejdes der primært med at addere brøker med ens nævner med hinanden.
Fase 2
At addere to brøker med samme nævner ved at addere tællerne med støtte i konkrete materialer.
Brøkbrikker
Et eksempel på en opgave kan være, at læreren på tavlen introducerer brøken $\frac{1}{2}$ repræsenteret som en brøkblok, altså et rektangel. Læreren spørger eleverne: "Kan I finde på måder, hvor andre brøker lagt sammen kan give en halv?" Der indledes en samtale med klassen, hvor eleverne kommer med forslag; fx $\frac{1}{4} + \frac{1}{4} = \frac{2}{4}$.
De forskellige forslag bliver samlet op på tavlen; fx $\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} = \frac{4}{8} = \frac{1}{2}$. En central pointe er at forstå, hvorfor $\frac{1}{4} + \frac{1}{4} = \frac{2}{4}$. Det bør ligge i forlængelse af elevernes opbyggede forudsætninger med at forkorte og forlænge (ækvivalente brøker). Herefter arbejder eleverne videre i grupper med afsæt i de konkrete materialer som brøkbrikker eller papirstrimler til at finde andre brøker, som lagt sammen giver $\frac{1}{2}$ (se Figur 7). De skal tegne eksemplerne (brug evt. brøkbrikkerne som skabelon eller cirkelbrikker) og skrive regnestykket op.
Læreren samler op ved at trække eksempler op på tavlen.
Først trækkes de eksempler frem, hvor stambrøkerne indgår, som forslag til løsningen af opgaven. Fx $\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} = \frac{4}{8} = \frac{1}{2}$ og $\frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{3}{6} = \frac{1}{2}$. Der indledes en klassesamtale om, hvorvidt vi kan finde flere eksempler, hvor vi bruger stambrøker til at lave en halv. Hvornår kan vi få lagt stambrøkerne sammen, så vi kan få summen en halv? Hvornår kan vi ikke?
Herefter trækkes de eksempler frem på tavlen, som ikke er stambrøker, fx $\frac{2}{8} + \frac{2}{8}$ eller $\frac{2}{6} + \frac{1}{6}$. Det er stadig vigtigt, at tegningerne og de konkrete materialer danner afsættet for undersøgelsen.
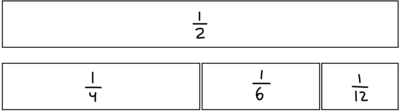
Hvis eleverne kommer med eksempler som $\frac{2}{5} + \frac{1}{10}$ eller $\frac{1}{4} + \frac{1}{6} + \frac{1}{12}$, hvor der er forskellige nævnere, kan læreren også inddrage disse eksempler og stille spørgsmål som: "Hvordan kan vi forklare og beskrive det, vi ser?" Eleverne skal ikke nødvendigvis nå til at finde fællesnævner gennem brugen af det rene symbolsprog endnu. Eleverne må gerne argumentere ud fra undersøgelserne i de konkrete materialer eller tegning. Det kan være, at eleven viser, at $\frac{1}{4} + \frac{1}{6} + \frac{1}{12}$ har nøjagtig den samme længde som $\frac{1}{2}$ i brøkbrikker (se Figur 8).


Fase 3
Fase 3, der strækker sig over en uge (4 lektioner), skal ligge i umiddelbar forlængelse af fase 2. I denne fase arbejdes med additionsstykker, hvor blot den ene af brøkerne skal omskrives for at finde en fællesnævner. Det centrale er, at eleverne oplever behovet for at finde en fællesnævner for at kunne finde den nøjagtige sum af to brøker.
Det er centralt, at der altid tages afsæt i brøker, som eleverne har en klar fornemmelse af størrelsen på, fx $\frac{1}{4} + \frac{3}{8}$. Hvor stort vil resultatet være? Vil det blive større eller mindre end $\frac{1}{2}$?
Fase 3
At addere to brøker, hvor den ene nævner går op i den anden, med støtte i forskellige repræsentationer og regneudtryk.
Brøkbrikker
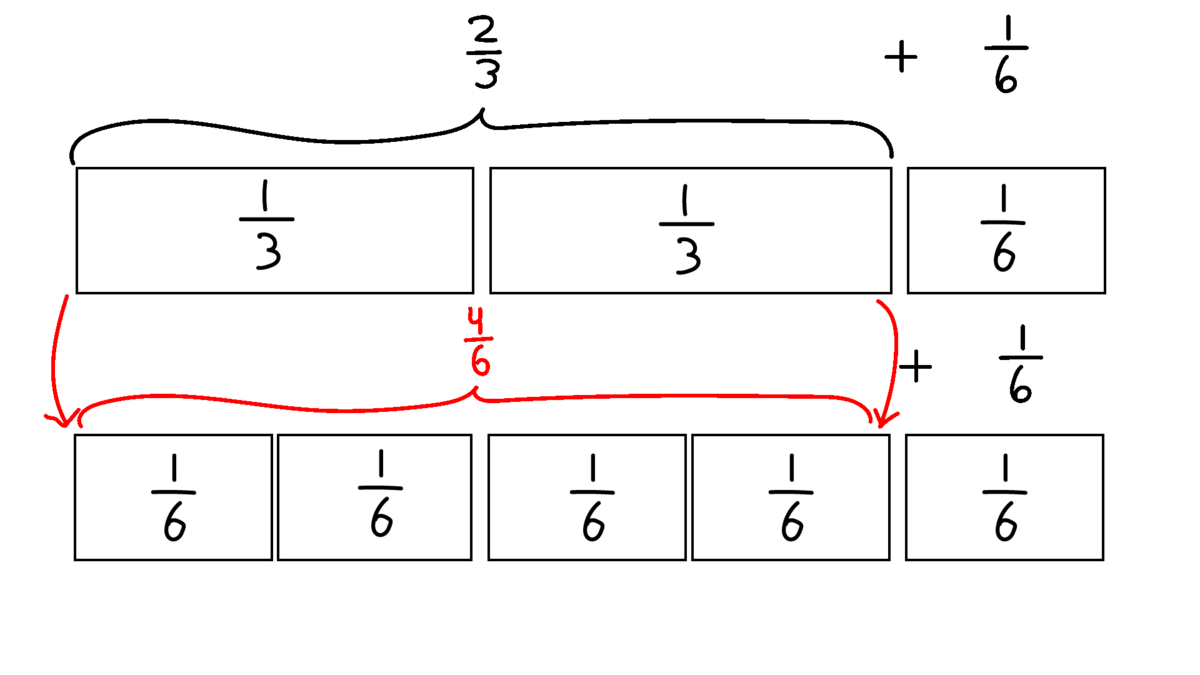
Eleverne skal igen forklare og bruge brøkbrikkerne eller tegne for at vise og forklare, hvad resultatet kan være af opgaven – og vise det på forskellige måder. Kan vi omskrive den ene af brøkerne for at finde en fællesnævner? Fx i opgaven $\frac{2}{3} + \frac{1}{6}$ kan eleverne lægge de to addender op efter hinanden ved at bruge brøkbrikker eller papirstrimler (se Figur 9). Opgaven er nu at finde den samlede længde, brikkerne angiver nøjagtigt. Eleverne arbejder videre med stykker, hvor de skal omskrive blot den ene af brøkerne for at finde en fællesnævner gennem arbejdet med de konkrete materialer. Det kan være stykker som:
$\frac{1}{2} + \frac{1}{6}$, $\frac{3}{8} + \frac{1}{4}$, $\frac{1}{10} + \frac{2}{5}$, $\frac{3}{12} + \frac{1}{4}$.
Læreren samler op på løsningen af de fire stykker. Hvilke strategier har eleverne brugt for at finde summen? Der vil være elever, som kun har brugt brikkerne. Andre kan efterhånden se på tallene og se, at vi kan lave 'mindre dele' af den ene brøk, så det passer, så det kan lægges sammen med den anden ved blot at se på nævnerne. De forskellige måder omtales, og eleverne støttes i deres fokus på nævnernes centrale betydning.
Læreren fortæller, at han lige har talt med sin søster i går (eller en anden opdigtet person), hvor hun sagde, at $\frac{1}{4} + \frac{1}{2}$ er $\frac{2}{6}$? Er det ikke også rigtigt? Han beder eleverne ræsonnere gennem forskellige konkrete materialer og tegninger, hvorfor $\frac{1}{4} + \frac{1}{2} = \frac{3}{4}$ og ikke $\frac{1}{4} + \frac{1}{2} = \frac{2}{6}$, så han kan forklare sin søster, hvad der er rigtigt. Eleverne kan eventuelt optage en film med deres mobil, hvor de skal forklare lærerens søster, hvad der er rigtigt eller forkert.
Fase 4
Fase 4 kan med fordel ligge i umiddelbar forlængelse af fase 3. Fasen strækker sig cirka over en uge (4 lektioner), og efterfølgende vil det være en god idé med en uge, hvor subtraktion indgår. Eleverne arbejder videre med brøkbrikkerne, men nu er det begge addender, der skal omskrives for at finde en fællesnævner.
Fase 4
At addere to brøker, hvor begge brøker skal forlænges for at finde fællesnævner med afsæt i selve regneudtrykket.
Finde fællesnævner
Stykket $\frac{1}{4} + \frac{1}{3}$ skrives op på tavlen. Der indledes med en klassesamtale om, hvordan vi kan lave en regnehistorie, der passer til stykket. Eleverne skal parvis finde på en regnehistorie, som kan passe til opgaven, og disse samles op i en klassesamtale, hvor de forskellige regnehistorier præsenteres. Der tales videre om: Hvad tror vi resultatet cirka er? Er det omkring $0$, $\frac{1}{2}$ eller $1$? Hvorfor? Herefter skal eleverne forsøge at komme med bud på, hvad summen af de to brøker nøjagtig kan være. Hvordan kan vi løse opgaven, hvis vi gerne vil finde det præcise resultat? Hvordan får vi lagt de to brøker sammen, når de ikke har samme nævner? Eleverne får brøkbrikkerne til at undersøge, hvordan man kan omskrive hver af de to brøker. Der samles op: Hvordan kan vi finde summen? En måde at støtte eleverne er at tage afsæt i den viden, de opbyggede i fase 1 og 2. Hvis vi nu lagde $\frac{1}{4} + \frac{1}{4}$ sammen, hvad giver det så? Er $\frac{1}{3} + \frac{1}{3}$ større eller mindre end $\frac{1}{4} + \frac{1}{4}$? Hvad kan vi sige om summen af $\frac{1}{4} + \frac{1}{3}$? Hvordan kan vi finde frem til den præcise størrelse, hvis vi bruger brøkbrikkerne?
Opgaven bliver skrevet på tavlen og vist løst gennem de konkrete materialer. Under hver brøk skrives den forlængede – så er der en klar sammenhæng mellem hver af de oprindelige addender og de nye forlængede. Det kan være, at nogle elever kommer med hypotesen om, at vi kan gange de to nævnere med hinanden for at finde den nye fællesnævner, men det er ikke centralt at nå til det før i slutningen af denne fase – målet her er, at eleverne først opbygger en forståelse af, at først 'forlænger' vi begge brøker og ser, hvornår vi får den samme nævner. (Der vil være elever, som stadig har brug for at bruge konkrete materialer for at forstå de størrelser, de regner med). Herefter arbejder klassen videre med at addere andre brøker. Fx:
$\frac{1}{2} + \frac{1}{3}$, $\frac{1}{4} + \frac{2}{3}$, $\frac{1}{2} + \frac{2}{5}$
Hvert enkelt stykke samles op på tavlen. Nu er det muligt at se mønsteret; at vi kan finde en fællesnævner ved at gange nævnerne med hinanden – og herefter forlænge de enkelte brøker i additionsopgaven, så de får en nævner, de kan være fælles om. Det er vigtigt, at eleverne får mulighed for at gentage og forklare, hvorfor man kan gøre dette. Det kan ske gennem optagelser på mobilen, at skrive reglen ned i en formelsamling, at tegne den eller skrive den ned i en logbog.
Der arbejdes med at konsolidere den nye viden gennem forskellige additionsstykker, hvor der er ens nævner, hvor man kun behøver at omskrive den ene brøk, og hvor man skal omskrive begge brøker. Det er vigtigt, at eleverne ser på brøkerne, som indgår i stykkerne, og vurderer, hvad der kan være smart.
Det kan være en idé at arbejde videre med en opgave som $\frac{1}{6} + \frac{1}{4}$, hvor vi kan finde en fællesnævner, som er mindre end $24$, nemlig $12$. Hvorfor kan vi det? Og kan vi finde mange forskellige fællesnævnere?
Den generelle metode:
$\frac{a}{b}+\frac{c}{d}=\frac{ad}{bd}+\frac{bc}{bd}=\frac{ad+bc}{bd}$