At addere brøker
Introduktion
Læringssporet retter sig mod en klasses udvikling af strategier til at addere to brøker. Sporet henvender sig til 4. eller 5. klasse og ligger i forlængelse af læringssporet ’At forstå brøker’. Set i forhold til stofområdet ’tal og algebra’ i grundskolen vedrører sporet rationale tal og addition som vist på Figur 1.
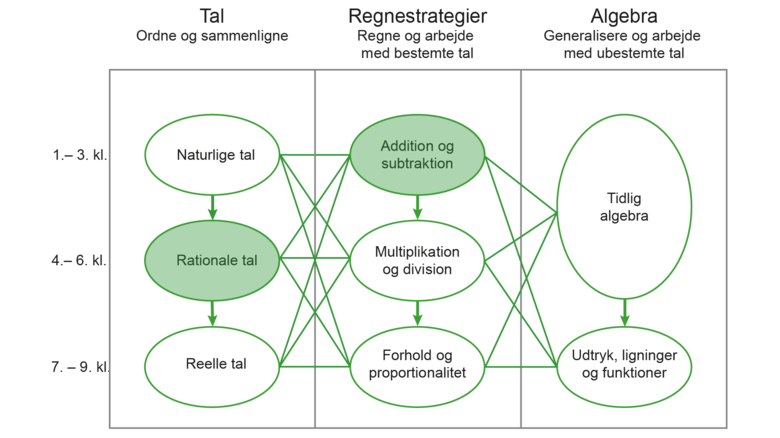
Læringsspor til grundskolen udviklet af NCUM under den fælles indsats for tal og algebra.
Udgivet 2025
Forfattere på læringssporet er Pernille Ladegaard Pedersen, Charlotte Krog Skott, Morten Blomhøj, Thomas Kaas og Marit Hvalsøe Schou.
Brøker, som indgår i dette læringsspor, er de positive, rationale tal. Altså $\frac{a}{b}$, hvor både $a$ og $b$ er naturlige tal og $b \neq 0$.
Mål
Læringssporet har to overordnede mål, som hænger sammen:
- Det skal bidrage til, at elever udvikler deres forståelser af addition med brøker.
- Det skal gøre elever i stand til at kunne addere to brøker.
Elever, der er kommet langt i forhold til mål 1, kan forklare, hvordan addition af brøker adskiller sig fra addition af naturlige tal. Det er grundlæggende, at eleverne forstår, at begge brøker, der repræsenterer forskellige opdelinger af det samme hele, ikke kan adderes direkte, og at det er nødvendigt at etablere en fællesnævner. Endvidere er det vigtigt, at de har en indsigt i, at det underliggende hele, som brøkerne er taget af, er ens. Forenklet sagt kan man ikke lægge $\frac{1}{4}$ familiepizza sammen med $\frac{1}{4}$ børnepizza. Elever, der er kommet langt i forhold til mål 1, kan også give et godt overslag på resultatet af en addition med ægte brøker. De ved fx, at resultatet af $\frac{1}{2} + \frac{2}{5}$ er lidt mindre end $1$.
Elever er kommet langt i forhold til mål 2, når de kan addere to brøker med forskellige nævnere. Et eksempel kan være, at en elev kan løse stykket $\frac{1}{6}+\frac{1}{4}$ ved at forlænge de to brøker, så de får en fællesnævner: $\frac{1}{6}+\frac{1}{4}=\frac{2}{12}+\frac{3}{12}=\frac{5}{12}$.
De to mål understøtter hinanden, og de udvikles i sammenspil. Forståelse af addition støttes ved at udføre additionen og omvendt – forståelsen støtter udførslen. Derudover kræver begge mål indblik i bl.a. egenskaber ved regning med brøker, hvor særligt behovet for at kunne forlænge eller forkorte brøker er centralt, når man skal opbygge forståelsen for addition med brøker.