Tal og algebra i indsatsen
Tal og algebra er tæt forbundet. De tal, vi anvender, når vi regner, er symboler, som står for fx kvantiteter eller antal. Det samme gælder de bogstaver, vi bruger i algebraiske aktiviteter. Forskellen er bl.a., at når vi bruger bogstaver, kan de repræsentere forskellige talværdier.
Gennem arbejdet med tallene i grundskolen skal eleverne udvikle talforståelse, der omfatter at:
- forstå tallenes opbygning og repræsentation, herunder titalssystemet og de forskellige talmængder
- have en fornemmelse for størrelsesordner
- have indsigt i de fire regningsarter, deres egenskaber og sammenhængene mellem dem
- kunne opstille og udføre beregninger med og uden hjælpemidler
- have en kritisk dømmekraft over for beregninger.
Talforståelse omfatter også, at eleverne kan regne fleksibelt med tallene og bruge andre strategier end standardalgoritmer. At regne fleksibelt betyder, at eleverne har opbygget og kan anvende et repertoire af regnestrategier og har udviklet blik for, hvornår det er smart og effektivt at bruge en eller flere af disse strategier (Fennema et al., 1996; Hickendorff et al., 2019).
Samtidig med og i forlængelse af at eleverne udvikler talforståelse, skal de også erfare betydningen af at kunne opstille og regne med bogstaver som symboler. En forståelse af symboler omfatter bl.a. at:
- erkende, at algebra er et værktøj, der gør det muligt at forstå, udtrykke og kommunikere om generelle sammenhænge
- udvikle en fornemmelse for de underliggende strukturer
- kunne udvikle og formulere algebraiske argumenter, fx i bevisførelse.
Der findes ikke en entydig definition af, hvad algebra – eller skolealgebra – er. Indsatsen er inspireret af det syn på algebra, som beskrives i Arcavi et al. (2016). Dette syn er baseret på forskning og harmonerer desuden med de danske styredokumenter. Algebra beskrives her både som en samling af emner, der bl.a. omfatter ligninger, formler og funktioner, og som bestemte måder at tænke og handle på. Algebraisk tænkning er centralt i indsatsen, og det beskrives som bl.a. at kunne:
- generalisere tal- og geometriske mønstre
- opstille og anvende formler
- omforme algebraiske udtryk
- opstille og analysere funktioner
- ræsonnere med algebraiske udtryk.
Læringssporene støtter elevernes udvikling af talforståelse, symbolforståelse og algebraisk tænkning gennem aktiviteter, hvor eleverne bl.a.:
- identificerer, beskriver og begrunder regneregler og sammenhænge
- opstiller regneudtryk og algebraiske udtryk
- regner fleksibelt med brug af forskellige strategier
- behandler symbolske udtryk, herunder løser ligninger
- fortolker og sammenligner algebraiske udtryk
- ræsonnerer og generaliserer med brug af tal og algebraisk notation, bl.a. ifm. bevisførelse
- oversætter og forbinder forskellige repræsentationer af det samme matematiske fænomen
- anvender funktioner til modellering.
Aktiviteterne tager udgangspunkt i centrale emner og begreber såsom de naturlige tal, brøker, ligninger og funktioner.
Læringssporene og styredokumenter
Læringssporene er forbundne med de gældende nationale styredokumenter for matematik i grundskolen (Børne- og undervisningsministeriet, 2019), gymnasiet og erhvervsuddannelserne. Læringssporene fokuserer imidlertid også på udvalgte områder af tal og algebra, som forskningen peger på som særligt vigtige.
I grundskolen gælder dette fx algebra på de yngste klassetrin, der er inspireret af forskning i tidlig algebra. Læringssporene har her især fokus på funktionelle sammenhænge mellem tal. Tidlig algebra betyder ikke – som navnet ellers kunne antyde – at man begynder tidligt i skolen med den algebra, man ville have undervist i senere. Det betyder derimod, at elever tidligt skal have mulighed for at udvikle algebraisk tænkning, bl.a. ved at opdage, formulere og begrunde generelle sammenhænge og regneregler i situationer, som eleverne finder meningsfulde. To af læringssporene lægger således op til, at eleverne arbejder med lineære sammenhænge og løsning af ligninger allerede fra 2. og 3. klasse på måder, der er tilpasset disse klassetrin.
I gymnasiet er læringssporene begrænset til den indledende matematikundervisning i grundforløbet og i starten af studieretningen. Her lægges der op til en styrkelse og udbygning af elevernes algebraiske tænkning fra grundskolen. Læringssporene supplerer gymnasiets styredokumenter ved at have et øget fokus på den algebraiske struktur, der fx kommer til udtryk i de grundlæggende regneregler. På erhvervsuddannelserne tager læringssporene udgangspunkt i matematisk modellering i situationer, som svarer til elevernes valg af uddannelse. Læringssporene supplerer her fagbilaget med forslag til at arbejde med at undersøge, fortolke og argumentere for formeludtryk fra erhvervsfaglige sammenhænge.
De fleste læringsspor henvender sig til grundskolen, og i hvert af disse spor er der en figur, der placerer læringssporets indholdet i forhold til de senere års styredokumenter (se Figur 1).
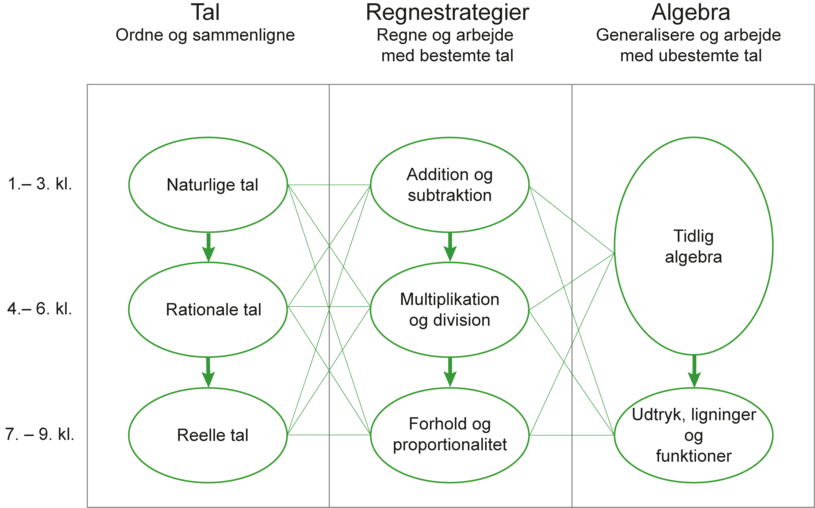
I Figur 1 er fagområdet tal og algebra opdelt i tre dele: tal, regnestrategier og algebra for henholdsvis indskolingen (1.-3. kl.), mellemtrinnet (4.-6. kl.) og udskolingen (7.-9. kl.). De tykke lodrette pile viser progressionen i arbejdet inden for hvert delområde gennem skoleforløbet.
De tynde streger viser, hvordan emner inden for de tre dele er forbundne. Eleverne skal altså bl.a. arbejde med hver af regningsarterne inden for alle tre talmængder og i sammenhæng med tidlig algebra. De regnestrategier, der relaterer sig til forhold og proportionalitet, hviler på indskolingens og mellemtrinnets fokus på tallene i sammenhæng med de fire regningsarter og det, eleverne har lært inden for tidlig algebra. Dette arbejde fortsætter i algebraiske udtryk, ligninger og funktioner.
I hvert læringsspor til grundskolen er de emner, som læringssporet primært fokuserer på, markeret med grønt som vist i Figur 2. På den måde er det visuelt nemt at se, hvilke emner der lægges mest vægt på i et læringsspor. Figur 2 viser fx, at læringssporet ”At addere etcifrede tal”, som titlen antyder, handler om de naturlige tal og en klasses første arbejde med regnestrategier til addition. Ved at se på figurerne for alle læringssporene i grundskolen bliver deres sammenhæng og den faglige progression på tværs af dem tydelig. I læringssporene til de yngste klasser vil farvemarkeringerne være øverst som i Figur 2, mens markeringerne i læringsspor til de ældre klasser vil bevæge sig nedad langs de tykke pile.
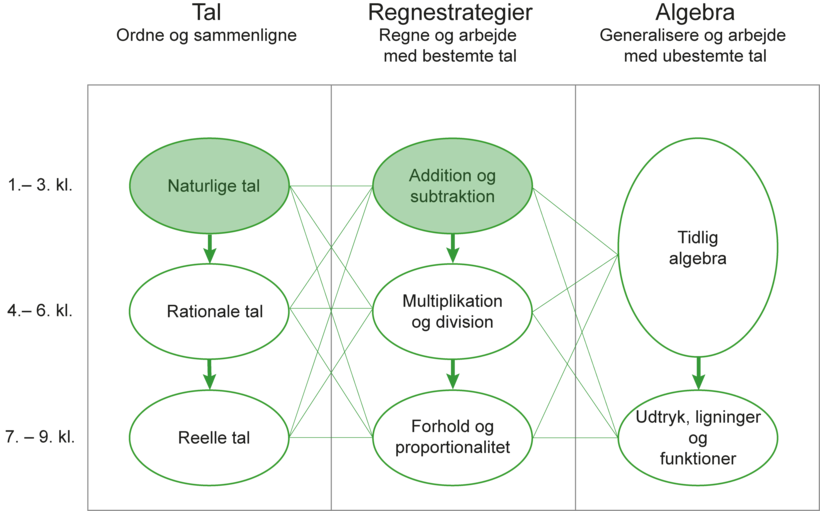
Læringssporene giver mulighed for at støtte eleverne i at udvikle alle de matematiske kompetencer (Niss & Jensen, 2002). Indsatsen er imidlertid ikke struktureret efter kompetencerne, og disse fremgår derfor ikke af Figur 1 eller Figur 2. Læringssporene er derimod udvalgt og organiseret efter stofmæssige kategorier.
Kilder
- Arcavi, A., Drijvers, P., & Stacey, K. (2016). The learning and teaching of algebra: Ideas, insights, and activities. Routledge.
- Fennema, E., Carpenter, T. P., Franke, M. L., Levi, L., Jacobs, V. R., & Empson, S. B. (1996). A longitudinal study of learning to use children’s thinking in mathematics instruction. Journal for Research in Mathematics Education, 27(4), 403–434. https://doi.org/10.2307/749875
- Hickendorff, M., Torbeyns, J., & Verschaffel, L. (2019). Multi-digit addition, substraction, multiplication and division strategies. In A. Fritz, V. G. Haase, & P. Räsänen (Eds.), International Handbook of Mathematical Learning Difficulties: From the Laboratory to the Classroom (pp. 543–560). Springer. https://doi.org/10.1007/978-3-319-97148-3
- Niss, M., & Jensen, T. H. (2002). Kompetencer og matematiklæring: ideer og inspiration til udvikling af matematikundervisning i Danmark. København: Undervisningsministeriet.