Eksempel: Trekantsberegning
I eksemplet skal eleverne arbejde med trekantsberegning ved at se på punkter, materiale, dimensionering og bæreevne i en skunkstolpe. Målet er at skabe genkendelighed for eleven, og det er et eksempel på en erhvervsfaglig opgave, der bygger bro mellem matematik og den erhvervsfaglige sammenhæng.
Spær til tømrer og Pythagoras
Dette er et eksempel på, hvordan man som lærer kan skabe erhvervsfaglige opgaver. Eksemplet er opbygget som i modellen vedr. den dobbeltrettede broforbindelse, hvor de tre trin, der skaber forbindelsen (bygger bro) mellem matematik og den erhvervsfaglige sammenhæng, er:
- Trin 1: Erhvervsfaglig emne-introduktion: Benævn matematikken med faglige begreber.
- Trin 2: Delt erhvervsfaglig og generisk gentagelse af introduktion: Benævn matematikken både med faglige begreber og generiske udtryk.
- Trin 3: Generisk gentagelse af introduktion: Benævn matematikken med generiske udtryk.
Læs mere om den dobbeltrettede broforbindelse i Modeller for samspil mellem matematik og erhvervsfag.
Trin 1
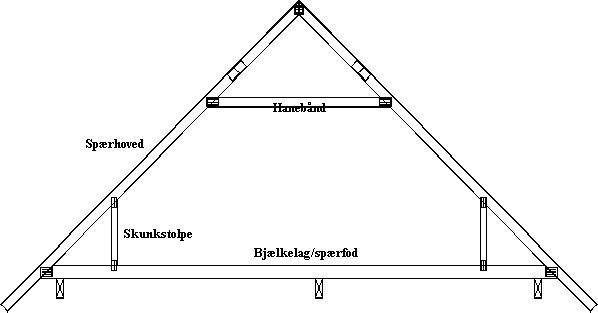
Opgaven i trin 1 er et fagfagligt virkeligt eksempel for eleven. Grundlaget i dette eksempel, er en ligebenet trekant, men introduktionen er faglig. Opgavens løsning bliver hjulpet af faglige begreber, eleven kender eller skal lære at kende. Der er flere matematiske elementer/matematiske emner, som eleven kan beskæftige sig med ud over skunkstolpen, fx punkter, materiale, dimensionering, bæreevne mv.

Målet her er at skabe genkendelighed/virkelighed for eleven ved trekantsberegning, sådan at fx et spærhoved kan betragtes som c-siden i en retvinklet trekant. Desuden åbner opgaven for at lave flere meningsfyldte beregninger inden for samme figur (punkter, materialer mv.).
Målet er også at overføre den faglige kunnen, eleven har eller opnår, til en mere almen eller generisk matematiske kunnen. Det vil sige, at elevens færdigheder til at udføre praktiske operationer i sin erhvervsfaglige undervisning som fx deling, inddeling, punktafsætning, vinkelbesnøring mm. kan bruges til at skabe bro mellem erhvervsfaglige sammenhænge og matematisk viden og kunnen.
Trin 2
Trin 2 er en imiteret praktisk opgave. Her stilladserer vi både elevens matematiske arbejde og elevens erhvervsfaglige arbejde. Udgangspunktet kan fx være et spørgsmål om, hvordan højden af en skunkstolpe afhænger af stolpefodens afstand til taget.
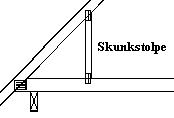 Det kan bruges både som en generisk problemstilling til arbejdet med retvinklede trekanter i matematik og til at kvalificere løsning af den praktiske opgave. I matematik kan det fx føre til undersøgelser ved hjælp af tegneprogrammer, hvor også betydningen af tagets hældning kan undersøges. I den virkelige situation kan brugen af matematik kvalificere valget af, hvor dyb skunken skal være og beregningen af, hvor høj stolpen så nødvendigvis må være, når dens montering tages i betragtning, jf. billedet til højre.
Det kan bruges både som en generisk problemstilling til arbejdet med retvinklede trekanter i matematik og til at kvalificere løsning af den praktiske opgave. I matematik kan det fx føre til undersøgelser ved hjælp af tegneprogrammer, hvor også betydningen af tagets hældning kan undersøges. I den virkelige situation kan brugen af matematik kvalificere valget af, hvor dyb skunken skal være og beregningen af, hvor høj stolpen så nødvendigvis må være, når dens montering tages i betragtning, jf. billedet til højre.
Eksemplet kan bruges både til en generisk og faglig introduktion samt til at læne os op ad faglige eksempler, når eleven oplever frustrationer. Eksempelvis kan vi hjælpe eleven med at overskue forskellige dele af en faglig disciplin som fx skunkstolpens højde som vist på billedet til højre. Beregningerne kan give mål, placeringer og vinkler mm., eleven kan bruge direkte i sit praktiske arbejde.
Trin 3
Trin 3 er et generisk og abstrakt eksempel for eleven i form af en ligebenet trekant. Vi kan betragte dens geometriske egenskaber som fx symmetri og beregne dens vinkler algebraisk ud fra opgivne mål.
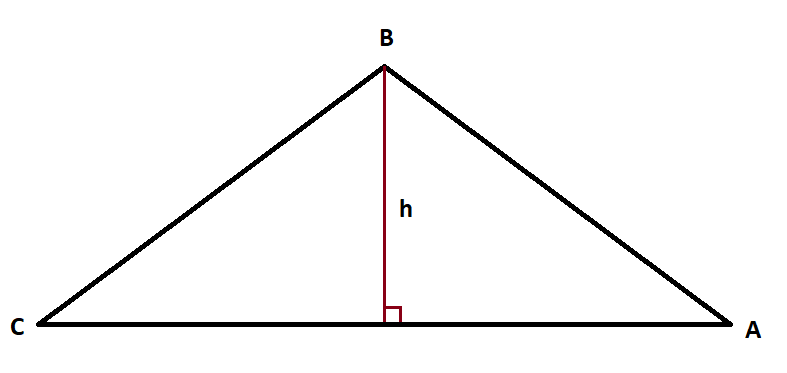 Den ligebenede trekant i sin abstrakte form kan enten være udgangspunktet for formulering af generiske geometriske problemer, der så kan konkretiseres i forhold til konstruktion af spær. Eller også kan den ligebenede trekant i sin abstrakte form være resultatet af en gradvis matematisering af konstruktion af spær.
Den ligebenede trekant i sin abstrakte form kan enten være udgangspunktet for formulering af generiske geometriske problemer, der så kan konkretiseres i forhold til konstruktion af spær. Eller også kan den ligebenede trekant i sin abstrakte form være resultatet af en gradvis matematisering af konstruktion af spær.
I begge tilfælde er det afgørende, at der skabes forbindelser mellem den virkelige (konkrete) situation og de matematiske repræsentationer i form af geometriske figurer og algebraiske beregninger. Vi ser det som målet med undervisningen, at eleven både kan opfatte den ligebenede trekant som model af en spærkonstruktion og spærkonstruktionen som en model for forståelse af en ligebenet trekant og dens egenskaber. Ofte bliver emner introduceret gennem en generisk præsentation, men for erhvervsskoleelever er det generelt vigtigt, at undervisningen er båret af faglige eksempler og referencer, som eleverne oplever som virkelige, eksempelvis skunkhøjden eller længden af et spær.
Eksempler på andre faglige temaer

- Beklædningsinddeling for en tømrer.
- Valsning og udlæg for en smed.
- Masse, vægt og fart for en lastvognschauffør/transportfolk.
- Målfaste elevproducerede tegninger.
- Målfaste tegninger fra elevens erhvervsfaglige opgaver.
- Programmering/opstilling/kalibrering af div. maskiner
- Kapacitet gennem rør med eller uden tryk.
- Dimensionering af ledninger ift. strømstyrke.
- Samling af en VVS-installation, jf. billedet. Stil fx spørgsmålet:
- I hvilken rækkefølge kan den være samlet?
Gode råd og refleksion
Den praktiske matematikopgave motiverer eleverne på erhvervsskolerne. Når underviseren i matematik skal tematisere eller producere sådanne opgaver og/eller aktiviteter, er det en fordel at gøre dette i et tværfagligt samarbejde. Derved vil eleven opleve virkelige, uformelle og konkrete eksempler fra elevens erhvervsfag. Sådanne opgaver kan for eksempel basere sig på opgaver og praksisser fra elevens praktik.
Fem gode råd fra praksisser
- Introducér matematiske emner som aspekter af elevernes fag.
- Opgaven skal i sin form/genstand være genkendelig fra den faglige undervisning.
- Brug begreber og sprog fra erhvervsfaget til at forklare beregningsmetode og -mål.
- Opgaven skal være en bro til almen matematisk forståelse og kompetence.
- Arbejdet fra matematikundervisningen bruges enten til at løse eller forberede praktiske opgaver i den erhvervsfaglige undervisning.
Ovenstående kan fungere som punkter til inspiration ved udvikling af opgaver og aktiviteter.
Refleksionen
Når opgaverne er samlet fra et erhvervsfag, kan det anbefales at samarbejde med en anden matematikunderviser om at bryde de faglige opgaver ned i enkelte matematiske opgaver, således at de kan stilladseres gennem en gradvis matematisering. Det giver indblik i elevens fag og praktik, men giver også mulighed for at udvide opgaven matematisk.
Det anbefales ikke, at man sigter en praktisk opgave mod et bestemt sted i pensum i matematik, men i stedet at man søger at afdække, hvilke forskellige matematiske tilgange, der kan være relevante. De fleste faglige praktiske opgaver breder sig nemlig ud over flere matematiske emner. Og opgaver, der er målrettet bestemte matematiske emner, kan let ende med at blive opfattet af eleverne som søgte og uvirkelige og dermed mindre motiverende.
til: ERHVERVSKOLE
emne: EKSEMPLARISKE OPGAVER TIL SAMSPIL MELLEM MATEMATIK OG ERHVERVSFAG
UDGIVET: 2021