Modellering i læreplanerne
Læreplaner og kompetencer
Læreplanene for EUD omtaler ”De centrale kompetencer i matematik”, og de otte kompetencer fra den såkaldte KOM-rapport nævnes (Kompetencer Og Matematik). Kilde 1
Det er den rapport fra Undervisningsministeriet, hvori matematikbeherskelse for første gang blev bestemt i termer af en række specifikke kompetencer og dermed rækker ud over sædvanlige indholdsdiscipliner (tal, algebra, geometri osv.). Kilde 2
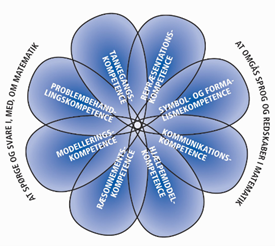
De otte matematiske kompetencer går på tværs af matematiske discipliner og består af: Modelleringskompetencen, Problembehandlingskompetencen, Symbol- og formalismekompetencen, Repræsentationskompetencen, Tankegangskompetencen, Kommunikationskompetencen, Hjælpemiddelkompetencen og endelig Ræsonnementskompetencen. De grupperes nogle gange i to overordnede grupper. Disse otte kompetencer og grupperingen i to illustreres ofte ved kompetenceblomsten (Figur 1).
I Danmark er kompetencerne blevet brugt som grundlag for udvikling af læreplaner i matematik på mange forskellige uddannelsestrin, specielt ift. kompetenceorienteret matematikundervisning. En udvikling i retning af kompetencebaseret læreplaner ses parallelt i mange andre lande, f.eks. Holland og USA, og i Norge har KOM-rapporten spillet en stor rolle for forståelsen af matematiske kompetencer.
Hvad er fordelene ved matematisk modellering i undervisningen?
I dette tema er fokus på modelleringskompetencen og dens ligheder og forskelle med problembehandlingskompetencen. Når man bruger matematik til løsning af problemer i erhvervsfagene, involverer det i praksis brug af modeller, hvilket ofte kræver matematisk problemløsning. Derfor er modellerings- og problemløsningskompetence vigtig i matematik i EUD. De to kompetencer kan samtidig motivere og støtte læringen af matematik. Det er baggrunden for, at både modellering og problembehandling/problemløsning er en del af læreplanerne i Danmark og i mange andre lande.
Den britiske statistiker, George Box, er berømt for citatet: ”All models are wrong, but some models are useful” - altså at en matematisk model aldrig vil være 100% korrekt. En matematisk model vil derfor altid netop være en model, men ikke hele sandheden. Modellen er ikke bedre end de antagelser, man gør sig undervejs i modelbygningen. Men hvorfor så have modellering som en del af ”pensum”? Skal matematik ikke kunne ”regne rigtigt”, ellers kan vi da ikke regne med den? angiver en række grunde til at undervise i modellering. Kilde 3
- En ”pragmatisk forklaring”, som siger, at for at vi som mennesker kan blive i stand til at forstå og mestre virkelighedssituationer, så må passende eksempler på opstilling og anvendelse af modeller behandles i undervisningen.
- En ”formativ forklaring”, hvor kompetencer læres ved at være engageret i dem, og specielt kan matematisk modellering kun læres ved at blive aktiveret i en sådan proces.
- En “kulturel forklaring”, hvormed menes at for at forstå matematikken som en videnskab, skal man også møde verdenen uden for matematikken.
- En “psykologisk forklaring”, da mødet med virkelige eksempler kan (1) øge elevers interesse for matematik, (2) det kan motivere og strukturere matematisk indhold og (3) kan lede til bedre forståelse af det, og (4) at det huskes længere. De fire punkter under den psykologiske forklaring er vægtige argumenter til fordel for modellering.
I en blog på American Scientist beskriver fem grunde til at bruge modellering i undervisningen. Kilde 4
Disse er baseret på egne erfaringer, men passer meget godt på Blums argumenter:
- Standard problemløsning er kedeligt, men modellering giver mulighed for ægte valg.
- Ingen kan lide at tage fejl – men i modellering er der mange gyldige svar.
- Modellering af ægte/virkelige? problemer kan gøre en forskel for elevernes motivation og læring i forhold til brugen af skolebogsproblemer.
- Matematik er svært og kræver øvelse, men modellering giver anledning til kreative løsningsprocesser.
- Matematik kan være ensomt men modellering er en team-sport.
Man kan måske sige, at modellering i skolen har både ”positive” argumenter, f.eks. at forberede elever på at forstå virkeligheden bedre, og ”negative” argumenter som at undgå at elever mister interessen for matematik. Begge dele gør sig også gældende for elever på erhvervsuddannelser. Læs evt. mere her om hvilken rolle motivation spiller på erhvervsskoler.
På et mere samfundsmæssigt plan handler modellering også om dannelse. Maass m.fl. argumenterer for, at COVID-19 epidemien viste, at borgere verden over er nødt til at vide, hvilken rolle matematik spiller i processen med at forstå og håndtere globale udfordringer. Borgere, og deres ledere må forstå, at forudsigelser som eksempelvis antallet af mulige omkomne er baseret på modeller, der hviler på antagelser og den anvendte datamængde. Kilde 5
Politiske beslutninger med langtrækkende virkning tages bl.a. på baggrund af output fra matematiske modeller. Modellerne skal derfor kritisk evalueres og upræcisheder skal håndteres og vurderes. Elever skal også vide, at det er muligt med empirisk kontrol af modeller, og evt. afprøve dette som led i undervisningen. Disse evner og viden om matematisk modellering er et centralt element af medborgerskab.
Kilder
1. Fagbilag, vejledning og prøver | emu danmarks læringsportal (Se vejledning 2020).
2. Niss, M. & Jensen, T. H. (2002). Kompetencer og matematiklæring – ideer og inspiration til udvikling af matematikundervisning i Danmark. Uddannelsesstyrelsens temahæfteserie nr. 18. København: Undervisningsministeriet.
3. Blum, W. (2015). Quality Teaching of Mathematical Modelling: What Do We Know, What Can We Do? I S. J. Cho (Red.), The Proceedings of the 12th International Congress on Mathematical Education (pp. 73–96). Springer International.
4. Levy, R. (2015). 5 Reasons to Teach Mathematical Modeling. American Scientist Blog. https://www.americanscientist.org/blog/macroscope/5-reasons-to-teach-mathematical-modeling
5. Maass, K., Artigue, M., Burhardt, H., Doorman, M., English, L. D., Geiger, V., Krainer, K., Potari, D. & Schoenfeld, A. (2022). Mathematical modelling – a key to citizenship education. I: N. Buchholtz, B. Schwarz & K. Vorhölter (Red.), Initiationen mathematikdidaktischer Forschung (pp. 31-50). Springer Spektrum, Wiesbaden.
til: ERHVERVSUDDANNELSER
emne: MATEMATISK MODELLERING PÅ ERHVERVSSKOLER
UDGIVET: 2022