Eksempel: Undersøgende aktivitet i statistik - 6. klasse
I det følgende eksempel på undersøgende matematikundervisning skal eleverne sammenligne en ny behandlingsmetode til AIDS-patienter med en tidligere metode.
Aktiviteten er afprøvet i forbindelse med et forskningsprojekt om statistik i USA. Eleverne var en amerikansk 7.-klasse, hvor eleverne er 12 år, hvilket svarer til en dansk 6.-7.-klasse. (Kilde 1)
AKTIVITETENS FAGLIGE FOKUSPUNKTER
- Eleverne skal se på fordelinger af data.
- Eleverne skal arbejde med autentisk dataanalyse.
- Eleverne skal lære at tænke i relative forskelle i stedet for absolutte forskelle.
1. Iscenesættelse
Læreren iscenesætter aktiviteten ved at sætte eleverne ind i det problem, som de skal undersøge:
Der er udviklet en ny behandlingsmetode til AIDS-patienter. Behandlingens virkning kan undersøges ved at måle patienternes T-celletal.
Jo højere T-celle-tal, jo bedre virker behandlingen.
I kan se data fra de to patientgrupper herunder. I det øverste diagram er data fra de 46 patienter, der har modtaget den nye behandling, i den nederste er data fra 186 patienter, der har modtaget den gamle behandling.
Problem: Sammenlign virkningen af de to typer behandling. Hvilken behandling er bedst?
2. Undersøgelse
Aktiviteten går ud på, at eleverne sammenligner de to behandlinger med udgangspunkt i de to diagrammer. Eleverne arbejder sammen i par, mens læreren går rundt og taler med dem, stiller og besvarer spørgsmål og udfordrer.
De fleste elever konstaterer umiddelbart, at den nye behandling er bedre end den gamle.
En elev siger:
"Næsten alle patienter med den nye behandling har over 550, og næsten alle med den gamle behandling har under 550, så den nye behandling er bedst."En anden elev siger:
"Hvis man kigger på diagrammerne, har den nye behandling en bakke fra 550 til 730, og den gamle har en bakke fra 250 til 550."
Herefter er elevernes fokus at beskrive generelle forskelle på de to datasæt. Læreren støtter eleverne i at konstruere forskellige notationsformer og diagrammer, de kan bruge til at beskrive og sammenligne de to datasæt. Det kan fx være brugen af termen 'bakker' om diagrammet i figur 1 (se nedenfor). Samtidig vælger læreren nogle forskelligartede elevsvar ud, som skal præsenteres ved fællesgørelsen.
3. Fællesgørelse
To elever præsenterer de to grafer i figur 1. De øvrige elever kommenterer præsentationerne.
Figur 1
Læreren stiller både spørgsmål til gruppen og til resten af klassen:
"Forstår I, hvad de mener?" og "Viser fremstillingen nogle vigtige ting?"Følgende dialog udspiller sig mellem læreren og en elev, som forsøger at forklare 'bakkerne' på diagrammet:
Sharon:
"Det, hun taler om, tror jeg, er det samme, som når du siger, at størstedelen (the majority) af tallene er på det sted, hvor det går opad."
Lærer:
"Jeg kan se, hvor det går op (peger på 'bakken' på det nederste diagram)."Sharon:
"Ja, lige der, det er der, de fleste er."
Herefter præsenterer en anden gruppe. Deres beskrivelse af datasættene kan ses i figur 2:
Figur 2
Ved diskussionen spørger læreren, hvorfor de har valgt at opdele ved netop 525.
Til det svarer eleverne, at det er fordi de fleste patienter, der har modtaget den gamle behandling, var under 525, og de fleste, der har modtaget den nye behandling, er over 525.
Under diskussionen foreslår en elev at tegne 'diagrammet' i figur 3:
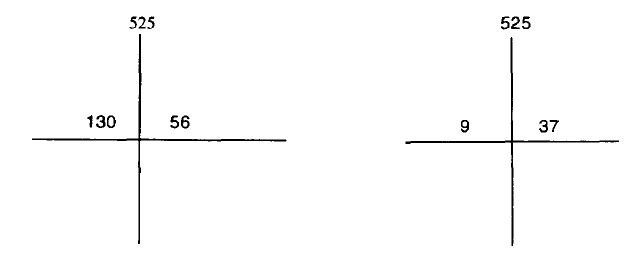
Figur 3
Efter præsentationerne vil læreren fokusere på forskellen mellem absolutte og relative forskelle, som er et af fokuspunkterne.
Derfor spørger hun:
"Kan man ikke sige, at diagrammet viser, at den gamle behandling virker bedst, fordi der var 56 patienter med T-celle-tal over 525, men her (peger på diagrammet til højre i figur 3) er der kun 37. Så den gamle behandling er bedre, fordi der er flere personer. Jeg mener, der er 19 personer mere."Eleverne argumenterer umiddelbart imod denne påstand med uformelle argumenter om forholdet mellem tallene.
For eksempel siger en elev:
"Jeg har et forslag. Jeg ved ikke, hvordan man gør det (uforståeligt). Er der en måde at sammenligne 130 og 56 med 9 og 37. Jeg ved ikke hvordan."
Herefter foreslår læreren 'procentdele', og i den følgende dialog udregner en del elever den procentvise andel af patienter over og under 525 i begge fordelinger. Diskussionen munder ud i, at der er enighed i klassen om, at det generelt er hensigtsmæssigt at beskrive forskelle på to datasæt med relative tal frem for absolutte tal.
De tre diagrammer er tegnet af eleverne. Dialogen er oversat af denne artikels forfatter. Eksemplet findes i Kilde 1
TIL OVERVEJELSE I FAGTEAMET
- Hvordan forventer I, at jeres elever vil sammenligne de to datasæt?
- Hvilke idéer fra aktiviteten kan I umiddelbart bruge/ikke bruge i jeres undervisning?
Fokuspunkter
Aktiviteten var tilrettelagt ud fra de tre faglige fokuspunkter:
1. Eleverne skal se på fordelinger af data
Et centralt fagligt element i aktiviteten er, at eleverne skal arbejde med fordelinger af data. Eleverne skal lære at opfatte et datasæt som en helhed, der består af talværdier fordelt inden for et afgrænset interval. Ved beskrivelsen og sammenligningen af de to datasæt er der desuden fokus på, at eleverne skal identificere overordnede generelle tendenser og mønstre og ikke kun se på enkeltelementer.
Ifølge forskerne giver det eleverne bedst mulighed for at udvikle forståelse for diagrammer og deskriptorer, når idéen med disse udspringer af den mere overordnede hensigt med at beskrive datasæt. For at matematiske (her statistiske) begreber kan blive opfattet som meningsfulde af eleverne, skal de være nødvendige og relevante i forhold til at løse problemer og ikke blot isolerede begreber løsrevet fra en sammenhæng. (Kilde 1)
Ved at skabe sammenhæng mellem proces og indhold lærer eleverne samtidig, hvilke statistiske metoder (herunder hvilke deskriptorer og diagrammer) der er velegnede til at beskrive eller behandle et givet problem.
2. Eleverne skal arbejde autentisk med dataanalyse
Problemstillingen er forsøgt formuleret sådan, at eleverne kommer til at arbejde autentisk med dataanalyse, det vil sige, at aktiviteten i klasseværelset ligner statistikerens arbejde. (Kilde 1)
Dette sikres blandt andet ved iscenesættelsen, hvor undersøgelsen skal gøres relevant og interessant for eleverne, således at de gennem hele aktiviteten forsøger at løse det konkrete problem.
Igennem hele forløbet opmuntrer og opfordrer læreren eleverne til at tale om det konkrete problem og den konkrete situation (med brug af data fra de konkrete datasæt) i stedet for 'blot' at tale om de statistiske data som tal.
Herudover forsøger læreren at få eleverne til at argumentere for deres påstande, så matematisk argumentation bliver 'autoriteten' frem for læreren eller lærebogen. Det er vigtigt, at eleverne bidrager med input i form af påstande, hypoteser og formodninger i undervisningen. Det er noget, de skal lære.
3. Eleverne skal lære at tænke i relative forskelle i stedet for absolutte forskelle
Et af de centrale faglige mål med aktiviteten er, at eleverne lærer at se på relative forskelle frem for absolutte forskelle, det vil sige, at et givet antal sættes i forhold til hele populationen.
I det foregående forløb havde forskerne endnu ikke observeret, at elever talte om relative forskelle. Derfor valgte de, at eleverne skulle sammenligne to datasæt af meget forskellig størrelse. Denne ændring betød, at en del elever efterhånden begyndte at bruge et sprog, der indikerede, at de tænkte i relative forskelle.
For at fokusere yderligere på denne tænkning, valgte læreren at stille et spørgsmål under fællesgørelsen, hvor hun sammenligner to absolutte værdier.
TIL OVERVEJELSE I FAGTEAMET
- Hvordan vurderer I relevansen af de tre faglige fokuspunkter?
- Hvilke forskelle og ligheder er der mellem de faglige fokuspunkter i aktiviteten, og det, I mener, der er vigtigt i undervisningen i statistik?
- Hvad gør efter jeres mening denne aktivitet til undersøgende matematikundervisning?
til: GRUNDSKOLE - 6. klasse
emne: UNDERSØGENDE MATEMATIKUNDERVISNING
UDGIVET: 2021
Forfatter
Kaj Østergaard
Lektor, ph.d.
VIA, Læreruddannelsen i Aarhus
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Cobb, P. (1999). Individual and collective mathematical development: The case of statistical data analysis. Mathematical thinking and learning, 1(1), 5-43.