Eksempel: At genbesøge negative tal i grundforløbet 1.g
Eksempel på et dansk lektionsstudie i gymnasiet om regning med negative tal. Se forløbet og lektionsplanen, der blev udviklet i forløbet.
Lektionsstudiet en del af TIME-projektet
To teams af matematiklærere fra Midtsjællands Gymnasium er med i EU-projektet Teachers´ Inquiry in Mathematics Education (TIME). Sammen med gymnasielærere fra Slovenien, Kroatien og Holland samt forskere i matematik og matematikdidaktik fra Danmark og de tre nævnte lande udvikler og afprøver de lektioner via lektionsstudier. Som inspiration benyttes Teorien om Didaktiske Situationer og en undersøgelsesbaseret tilgang til matematikundervisningen. TIME-projektet er startet i 2020, og det er første gang, at lektionsstudier bringes i spil på et gymnasie i Danmark.
PLANLÆGNINGSFASEN
I planlægningsfasen forberedes studielektionen. Idéer indsamles, og mål sættes. Derefter udvikler teamet i samarbejde en lektionsplan, der beskriver den planlagte studielektion. Og den indeholder også teamets bud på, hvilke strategier eleverne forventes at bruge til at løse de opgaver, der indgår i lektionen. Og der kan indgå bemærkninger om, hvad teamet særlig ønsker at observere.
Identifikation af problemet 'regning med negative tal'
Under en første drøftelse af de problemer, som det ene team oplevede i grundforløbet på STX, identificerede de regning med negative tal som en udfordring for mange elever.
"Eleverne har generelt problemer med at regne med negative tal, også ved addition."
- fra interview med deltagende lærer
Matematiklærernes erfaringer er, at et separat forløb om regnearternes hierarki virker demotiverende for eleverne. De plejer derfor at håndtere elevernes vanskeligheder med negative tal, når de opstår i den almindelige undervisning. Det fungerer imidlertid ikke optimalt, da det fjerner fokus fra det egentlige indhold. Teamet besluttede derfor at fokusere på regning med negative tal og at tage udgangspunkt i en regel, som elever ofte ikke husker tilstrækkeligt præcist fra grundskolen, og som de derfor er usikre på, hvornår de skal bruge, nemlig at 'minus og minus giver plus'.
Teamet identificerede to problemer for eleverne
- Hvad siger reglen præcist?
- Kan de lære at forstå den ved at begrunde den på forskellige måder?
Afprøvninger af lektionsplanen
Teamet gennemførte lektionsstudiet med to afprøvninger af lektionsplanen og med deltagelse af to matematikdidaktikere fra Københavns Universitet. I første studielektion var fokus på begge problemer, men der viste sig at være for lidt tid til, at eleverne kunne begrunde reglen. Derfor ændrede teamet lektionsplanen, så vægten i anden studielektion var på begrundelser – det andet problem. Med henblik på hurtigere at få reglen formuleret præcist valgte teamet derfor at indlede studielektionen med tre små regneopgaver. Se en udgave af den reviderede lektionsplan nedenfor.
Se lektionsplanen 'Minus og minus giver plus'
OBS: Lektionsplanen: 'Minus og minus giver plus', fra TIME-projektet 2020 er let revideret i forhold til planen i TIME-projektet, da vi i eksemplet har udeladt terminologi fra Teorien om Didaktiske Situationer.
| Deltagende lærere | Flóvin Tór Nygaard Næs, Katja Wagner og Bjarne Lund Pedersen. |
|---|---|
| Tilsigtet viden hos eleverne | At de udvikler bedre forståelser af negative tal og kan regne med dem. |
| Kompetencemål | - Symbol- og formalismekompetencen - Ræsonnement- og tankegangskompetencen |
| Nødvendige matematiske forudsætninger | Basal aritmetik. |
| Tid | 60 minutter. |
| Niveau | Grundforløb i starten af 1. g |
| Lektionens problemstilling | En gymnasieelev husker en regel fra matematiktimerne i grundskolen: ’Minus og minus giver plus’. Men hvad mener eleven egentlig med det? Og hvordan ville du forklare, hvorfor det egentlig hænger sådan sammen? |
| Fase | Lærerens handlinger inkl. instruktioner | Elevernes handlinger inkl. reaktioner |
|---|---|---|
| Intro (5 min) | Læreren stiller eleverne tre små regneopgaver på tavlen: \((-4) ⋅ 3\) \(5 ⋅(-2)\) \((-3) ⋅ (-5)\) | Eleverne løser opgaverne og taster svarene ind i det fælles læringsrum socrative.com. |
| PRÆSENTATION AF PROBLEMSTILLINGEN (5 min) | Læreren præsenterer problemstillingen og formulerer sammen med eleverne den præcise regel. Læreren opfordrer eleverne til at give gode forklaringer på, hvorfor minus gange minus giver plus, bl.a. ved at bruge de fire repræsentationsformer (sprog, formel, tabel og graf), som har været i fokus i grundforløbet. | Forventning om at eleverne nu kan formulere reglen præcist og bidrager til det. Eleverne lytter og stiller eventuelt afklarende spørgsmål. |
| GRUPPEARBEJDE OM AT GIVE BEGRUNDELSER (10 min) | Læreren går rundt og observerer, hvordan grupperne griber opgaven an. | Grupperne diskuterer forskellige begrundelser og skriver dem i Samarbejdsområdet i OneNote. |
| GRUPPERNE PRÆSENTERER DERES BEGRUNDELSER (10 min) | Læreren udvælger grupper med forskellige bud til at præsentere for klassen. | De udvalgte grupper præsenterer deres løsning. |
| VALIDERING AF BEGRUNDELSERNE (5 min) | Læreren drøfter og diskuterer de forskellige begrundelser med klassen. | Eleverne lytter og deltager med opklarende spørgsmål. |
| GRUPPEARBEJDE OM EN SELVVALGT BEGRUNDELSE (10 min) | Læreren opfordrer eleverne til at følge én idé, enten deres egen eller en af de andre gruppers, og præcisere den. | Grupperne vælger en begrundelse, som de forsøger at præcisere. |
| FÆLLES OPSAMLING (10 min) | Læreren samler op på de forskellige tilgange og præsenterer ud fra dem en begrundelse. Elevernes vanskeligheder med at argumentere matematisk bliver synlige, og læreren adresserer dem. | Eleverne lytter og deltager med opklarende spørgsmål. |
| OUTRO (5 min) | Lærer stiller tre opgaver, der minder om dem fra introsekvensen. | Eleverne regner opgaverne og taster dem ind i socrative.com. |
OBSERVATIONSFASEN
Observatørernes rolle ved studielektionen er at observere, hvordan studielektionen forløber, og specielt hvordan eleverne arbejder. De holder øje med, om lektionsplanens problemstilling og den tilsigtede viden opnås hos de elever, de observerer, og om de bruger andre strategier end dem, man havde forudset.
Kort beskrivelse af studielektionen 'Minus og minus bliver plus'
Som forventet fik læreren sammen med eleverne hurtigere formuleret reglen præcist i den anden studielektion. Faktisk svarede stort set alle eleverne korrekt på de tre indledende regneopgaver, ’og’ blev derfor hurtigt udskiftet med ’gange’.
I det første gruppearbejde kom eleverne op med mindst seks forskellige typer af forklaringer:
- Sproglige forklaringer baseret på dobbelt negation, fx:
”Jeg skal ikke ikke slappe af i dag.”
Dette var den hyppigste type af forklaringer, men også andre sproglige forklaringer blev givet:
”Jeg skylder to personer penge.” - Flere elever googlede en forklaring, som oftest også var sproglige huskeregler.
- Flere elever tegnede grafer for rette linjer i CAS med negative parametre, fx:
\(y=-x, y=(-2)⋅x\) og \(y=-2 ⋅ (-3)\) - Nogle elever brugte CAS til direkte at udregne forskellige stykker med negative tal.
- Få elever tænkte i arealbetragtninger, hvor de overgeneraliserede fra tilfældet med to positive sidelængder.
- Kun enkelte elever brugte en tallinje i deres forklaringer, som teamet ellers havde håbet på.
I den fælles opsamling startede læreren med at drøfte elevernes sproglige forklaringer og dernæst de geometriske forklaringer ud fra de rette linjer.
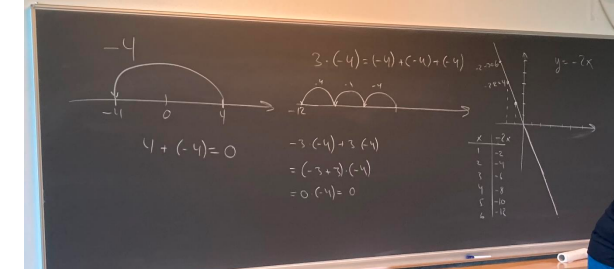
Billedet er taget i forbindelse med studielektionen. Kilde: Time-projects.eu
Her tilføjede læreren en tabel for \(y = (-2) ⋅ x \), hvor han startede mundtligt med de positive x-værdier, som han viste ud fra grafen, og dernæst de negative x-værdier ved brug af tabellen (se billede). Eleverne kunne gennemskue, at resultaterne for de negative x-værdier måtte være positive ud fra deres forhåndsviden om lineære funktioner.
Enkelte elever indvendte, at ingen af disse første forklaringer begrundede reglen.
Læreren introducerede dernæst en tallinje, først til at illustrere at \(4 + (-4) = 0 \) og dernæst til at vise, at \(3 ⋅ (-4) = -12 \). Det var eleverne med på.
Ved brug af disse regler gennemgik læreren et ræsonnement baseret på eksemplet \((-3) ⋅ (-4) + 3 ⋅ (-4) \), og efter udregningerne på billedet konkluderede han, "at så må \((-3) ⋅ (-4) = 12\)." Mange elever fandt det svært at forstå brugen af den distributive lov og dermed at forstå argumentet.
Alle eleverne regnede outro-opgaverne fuldstændigt korrekt.
REFLEKSIONSFASEN
Kort efter studielektionen samles teamet og reflekterer over det observerede. Refleksionssamtalen har en fast dagsorden, og deltagerne i teamet har hver deres rolle i samtalen. Det sikrer, at fokus holdes på studielektionens mål.
Læs mere om roller og dagsorden i: Hvad er lektionsstudier?
Refleksion efter studielektionen
Hvad lærte lærerne?
I den efterfølgende refleksion blev der rejst spørgsmål ved, hvor mange elever, der kunne følge ræsonnementet, særligt da nogle elever efter lektionen spurgte læreren, hvad forklaringen var. Det var teamets oplevelse, at kun de dygtigste elever forstod ræsonnementet, men at alle eleverne havde fået en fornemmelse af, hvordan man argumenterer i gymnasiet. Kernen i lektionen blev netop de vanskeligheder, som eleverne har med at arbejde på en anden, mere argumenterende måde, med matematik, end de har været vant til. Teamet vurderede, at lektionen var medvirkende til at bygge bro mellem folkeskole og gymnasiet på den måde, at det blev meget tydeligt, at fokus i gymnasiematematikken kan være noget helt andet, end eleverne er vant til. Dette blev af elever og lærere italesat helt konkret:
”Dette har vi lært på denne måde i folkeskolen.”
og
”Ja, nu skal vi se på det på en anden måde.”
Lektionen opfyldte altså det vigtige mål med grundforløbet, som er at skabe denne bro mellem folkeskolen og gymnasiet.
Selv om studielektionen ikke blev eksemplarisk i den forstand, at alle elever lærte det intenderede – hvad der i øvrigt sker sjældent, også sjældent i en studielektion – så gav lektionsstudiet anledning til en række værdifulde indsigter og refleksioner for lærerteamet.
Tre nye indsigter
En teoretisk udfordring
For det første lærte teamet noget om karakteren af det andet problem – at begrunde at produktet af to negative tal er positivt. Her bidrog matematikdidaktikerne fra KU med referencer til relevant matematikdidaktisk litteratur, som blev brugt i planlægningen. (Kilde 1)Teamet havde forgæves søgt efter et hverdagseksempel, der kunne forklare, hvorfor produktet af to negative tal er positivt. Litteraturen bekræftede, at der ikke findes et sådant eksempel, og reglen er speciel derved, at den alligevel læres i grundskolesammenhæng. For teamet var det nyt, at begrundelser for reglen er et internt matematisk problem, og at der er en teoretisk udfordring i at forklare reglen.
- Indsigt i elevernes forudsætninger
For det andet opnåede lærerne ny indsigt i, hvad eleverne havde med i deres matematiske bagage fra grundskolen – særligt ud fra de forklaringer de gav. Selv om eleverne gjorde sig mange gode overvejelser, blev det tydeligt:
”...at de manglede forudsætninger for at komme frem til det og viden om, hvordan man gør. Det er et internt matematisk problem, og det er nyt for dem at ræsonnere på denne måde.”
(Fra interview med en lærer fra teamet)
Teamet havde tænkt i hints i forhold til et emne om lineære funktioner, som eleverne lige havde haft, som fx at opstille en tabel og tegne en graf. I refleksionssamtalen kom der flere forslag til, hvordan læreren kunne have stilladseret elevernes arbejde med selve ræsonnementet, fx at en eller flere af de dygtigere elever genfortæller ræsonnementet for resten af klassen, eller at eleverne hver især går det igennem trin for trin guidet af nogle hjælpespørgsmål. - Idéer til nye studielektioner
For det tredje gav lektionsstudiet – og særligt de små justeringer fra første til anden studielektion – anledning til en række nye refleksioner og spørgsmål, som fx:
- Er det mere hensigtsmæssigt, at lektionsplanen opdeles i to studielektioner, så hver studielektion fokuserer på kun ét af de to problemer?
- Skabte studielektionen en nysgerrighed hos nogle elever efter at lære nye sider af matematikken at kende?
- Var de sidste fem minutter i outro givet godt ud, eller skulle læreren hellere have dvælet ved ræsonnementet og besvaret elevernes spørgsmål?
- Hvilke elevforslag var det hensigtsmæssigt, at læreren udvalgte til den fælles præsentation set i forhold til det ræsonnement, som var studielektionens mål?
Refleksion af mere overordnet karakter
Dette er et eksempel på, at et lektionsstudie, udover at lægge op til refleksioner relateret til konkrete undervisnings- og læringsproblemer også kan lægge op til refleksioner over problemer af mere overordnet karakter, som kan gå på tværs af uddannelsestrin.
I dette lektionsstudie er det overordnede problem, at elever i grundskolen skal lære at kunne bruge reglen om, at produktet af to negative tal er positivt. Og til en vis grad skal de også lære at forstå rationalet bag reglen – i modsat fald kan reglen blive til en tommelfingerregel, som eleverne let kan komme til at huske forkert, som vi så i eksemplet.
Eleverne kan imidlertid ikke lære at forstå reglen ud fra hverdagseksempler, som de ellers er vant til, men de kan få en fornemmelse for rationalet ud fra tabeller og grafer for rette linjer a la dem, der er anvendt i det aktuelle lektionsstudie.
Senere kan der så bygges videre på denne første matematiske forklaring med en begrundelse. Det spørgsmål, som rejses her, er, hvornår det er hensigtsmæssigt at præsentere eleverne for en matematisk begrundelse for reglen, fx en begrundelse baseret på formelle karakteristika ved tallene som i dette lektionsstudie?
til: GYMNASIE - grundforløb
emne: LEKTIONSSTUDIER
UDGIVET: 2021
Forfattere
Flóvin Tór Nygaard Næs
Midtsjællands Gymnasium
Charlotte Krog Skott
Docent
Københavns Professionshøjskole
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilde
Hefendehl-Hebeker, L. (1991). Negative numbers: Obstacles in their evolution from intuitive to intellectual constructs. For the learning of mathematics, 11 (1), 26-32.