Eksempler på modeller
Modeller er overalt
I vores hverdag er vi vant til at bruge sammenhænge mellem kvantitative størrelser mere uformelt, f.eks.: “Jeg vil gå 5 kilometer på 1 time” eller mere formelt, f.eks.: “Prisen starter på 100 kr., og dernæst koster det 16 kr. i timen”. I mere professionelle rammer kender vi f.eks. E = mc2, som er Einsteins formel for forholdet mellem energi (E) og masse (m) og lysets hastighed i vakuum (c). Alle disse relationer kan præsenteres både i ord, grafer, tabeller og formler – og de er alle matematiske modeller. Hvilken repræsentation man anvender, afhænger af hvad man ønsker at kommunikere og til hvem. Ligninger (så som Pythagoras) og tommelfingerregler (så som 3-4-5) er også modeller af virkeligheden. Matematiske modeller behøver ikke være store og indviklede programmer, som vi f.eks. ser i den makroøkonomiske model ADAM (Annual Danish Aggregate Model) udviklet af Danmarks Statistik, som består af ca. 2500 ligninger. Meget mindre kan også gøre det.
Hvordan beskrives en matematisk model?
De fleste mennesker har nemmere ved at fortolke grafer og tabeller end formler. Manipulation med formler, opskrivning af dem på andre former eller kombination af formler er en del af algebraen. Man behøver dog ikke altid anvende algebraiske udtryk til at udtrykke relationer mellem kvantitative størrelser eller løse problemer om relationer ved brug af kvantiteter. Kilde 1
Figur 5 viser eksempler på, hvordan samme matematiske model beskrives eller udtrykkes forskelligt. Til venstre på figuren ser vi tre repræsentationer af et bestemt forhold mellem x og y: algebraisk/ligning, tabel og graf. Til højre i figuren ses det samme for en anden relation, men hvor der i tillæg nederst til højre også ses en skriftlig repræsentation af modellen og en navngivning af typen af relation, nemlig lineært. (I parentes kan det måske bemærkes, at da relationen ikke går gennem Origo (0,0), er relationen ikke lineær men affin, men der er tradition for at kalde alle sammenhænge, hvis graf kan tegnes, som en ret linje for lineære.)
Hvis man googler f.eks. ordene “graf”, ”funktion” osv., og klikker på ”billede/image” får man mange sådanne eksempler. Overordnet set er alle formler modeller. Dvs. en formel, som giver mening i en virkelighedssituation, er en model af denne situation.
Forskellige repræsentationer
Laursen beskriver, baseret på Duval (2006), at en elevs problemer med at løse opgaver, hvori funktioner indgår, ikke nødvendigvis bunder i mangel på forståelse for funktioner, men i elevens forudsætninger for at bruge de forskellige repræsentationer som ligninger, grafer og tabeller. Kilde 2
Ifølge Duvall er der to grundlæggende matematiske processer: operationer og konversioner (konvertering/omdannelse). Kilde 3
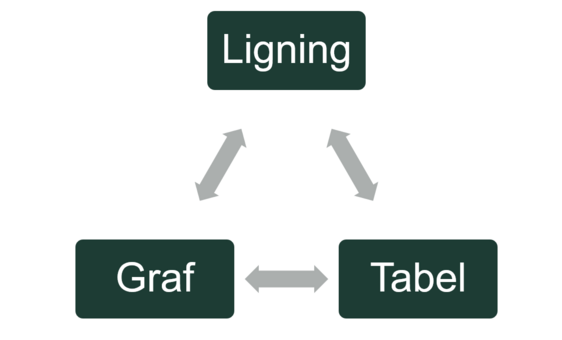
En konversion (se Figur 6) er en proces, der starter i en type repræsentation (f.eks. tabel) og ender i en anden (f.eks. en graf). Derimod er en operation en proces, der alene foregår inden for én type repræsentation. Det er centralt, at man som lærer undersøger, hvordan ens elever forstår og anvender de forskellige former for repræsentationer. I eksemplet i Figur 5 med cupcakes, så vi både en ligning (y = 2x – 4), en graf (graph) og en tabel (table). Nogle elever vil være mere ”hjemme” eller ”trygge” ved nogle repræsentationer end andre, men det er vigtigt, at de bliver trygge i alle, og i at skifte nemt mellem dem.
Hvad giver mening for elever på erhvervsskoler - eksempler
Forklaring af og eksempler på proportionelle relationer:
- Grafer altid gennem (0,0)
- Simple definitioner:
- Pris = 3 x antal timer
- Gåafstand i meter = 100 x antal minutter
- Se også:
Forklaring af og eksempler på invers/omvendt proportionalitet:
- Når farten går op, går rejsetiden ned
- Hvis fire mennesker kan male et hegn på tre timer, hvor lang tid vil det så tage seks personer at male det? Når antallet af malere går op, går tiden det tager at male ned. t = k/n (t = timer, n antal mennesker, k er proportionalitetskonstanten).
- Eksempler fra fysikformler, når en af variablene er givet. Ohms lov, U = RI, med U = 100 (f.eks.), og man skal finde strømstyrken: I = 100 / R.
- Se flere eksempler og forklaringer:
Lineære relationer som ikke går gennem (0,0) (også kaldet affine):
- H = 120 – 30 t
- Hvor lang tid tager det før H bliver 0.
To forskellige varer:
- P = 200 + 50t
- P = 150 + 60t
- For hvilke værdier af t er det billigere at købe den første?
Lineær men med flere størrelser involveret:
- H = 3G + 4K + 6 M
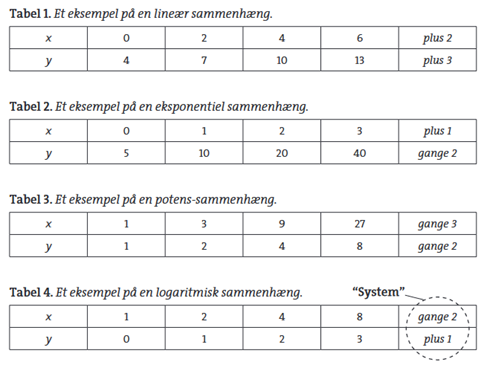
Oven for har vi beskrevet lineære sammenhænge, men mange matematiske relationer er ikke lineære, men logaritmiske, eksponentielle eller potenssammenhænge. Laursen (2008) har i den forbindelse angivet en model for, hvordan man kan forstå forskellige og ligheder mellem disse fire typer af sammenhænge (Figur 7).
Disse fire forskellige typer variabelsammenhænge/funktioner indgår rent faktisk i en spændende relation med hinanden, som måske kan hjælpe på forståelse af, hvad der kendetegner hver af dem – og måske herunder: hvad det særlige er ved lineære sammenhænge (se Figur 8). Her kommer det tydeligt frem, at f.eks. eksponentielle og logaritmiske sammenhænge opfører sig stik modsat – det samme med lineære- og potenssammenghænge.

Kilder
1. Goldin, G.A. (2014). Mathematical Representations. I: S. Lerman (Red.), Encyclopedia of Mathematics Education. Dordrecht: Springer. https://doi.org/10.1007/978-94-007-4978-8_103. Janvier, C. (Red.) (1987). Problems of representation in the teaching and learning of mathematics. Hillsdale: Erlbaum.Kaiser, G. (2014). Mathematical Modelling and Applications in Education. I: S. Lerman (Red.), Encyclopedia of Mathematics Education. Dordrecht: Springer. https://doi.org/10.1007/978-94-007-4978-8_103.
2. Laursen, N. N. (2008). Variabelsammenhænge i gymnasiets matematikundervisning. MONA 2008-4, 7–21.
3. Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131.
til: ERHVERVSUDDANNELSER
emne: MATEMATISK MODELLERING PÅ ERHVERVSSKOLER
UDGIVET: 2022