Test til kortlægning i starten af grundforløbet
Testning kan være en effektiv måde at få relevant information om eleverne ved starten af erhvervsuddannelsernes grundforløb, og det kan være et godt værktøj til at give et mere reelt billede af elevernes matematiske kompetencer og tydeliggøre matematikken som et aktivt værktøj.
Hvorfor test/kortlægning?
Undervisning og eksamen på grundforløb skal gennemføres i løbet af relativt kort tid. Derfor er der et behov for hurtigt at få indblik i elevernes profil, niveau og motivation. Det handler om at få et helhedsindtryk af elevernes viden og færdigheder samt af deres behov og motivation. Derved kan man bedre tilrettelægge og gennemføre en god undervisning.
Eleverne kommer med forskellige baggrunde. Nogle kommer direkte fra folkeskolen, og nogle har ikke været i et uddannelsessystem længe. Som lærer må man selv skaffe sig aktuel viden om eleverne. Testning af eleverne kan være en effektiv måde til at få relevant information om eleverne ved starten af grundforløbet, men der er en række forhold, som det er vigtigt at være opmærksom på. Ordet 'test' kan opfattes smalt, men vi anbefaler som princip at opfatte det bredt, så det fungerer som en 'kortlægning'.
Anvend erhvervsfaglighed, hvor det er muligt
Testningen skal give et bredt indblik i elevernes faglige forudsætninger, arbejdsmåder og oplevelser af tal og matematik i forskellige sammenhænge. Det er vigtigt, at eleverne kan bruge deres forskellige læringsstile i en ramme, der ligner det kommende erhverv. Det er vores erfaring, at de fleste undervisere primært tester med skriftlige opgaver, men vi anbefaler, at skriftlig testning ligeværdigt understøttes af praktiske-matematiske opgaver og matematiske opgaver samt spørgsmål som stilles og besvares verbalt.
Figuren nedenfor illustrerer princippet om, at man må bruge såvel verbale, skriftlige og praktiske tilgange for at få et helhedsindtryk af eleven.
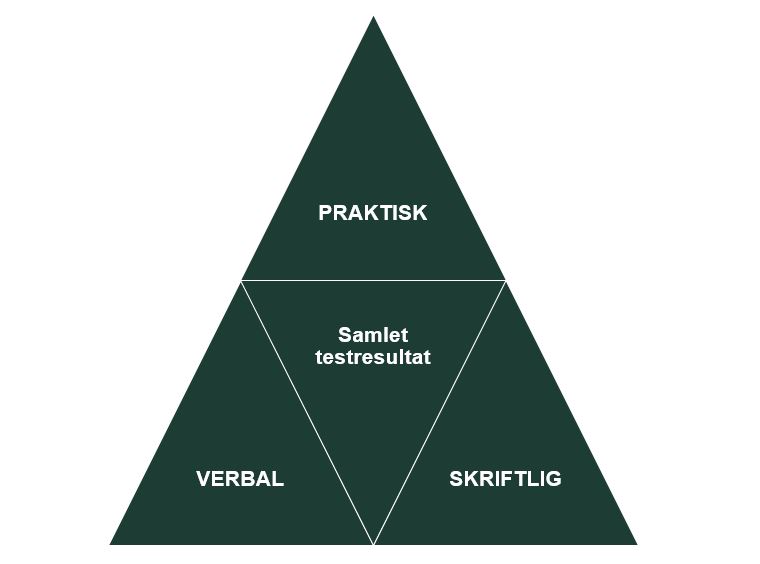
Figur 1: Kortlægningsmodel
Ud over at en bred testning kan give et mere reelt billede af elevernes matematiske kompetencer, så kan en bred tilgang også motivere for matematikken og tydeliggøre matematikken som et aktivt værktøj i elevernes kommende fag. En test kan således i sig selv bidrage til elevernes læring ved at vise, at matematik bruges på forskellige måder i erhvervet.
Kendetegn og eksempler på aktiviteter i testens tre hjørnetrekanter:
| Kendetegn | Forslag til opgaver | |
|---|---|---|
| Det praktiske | Er kendetegnet ved at indeholde fysiske materialer som eleven kan se som meningsfulde i et kommende erhverv. De stillede opgaver skal gerne fremhæve træk, der er typiske og karakteristiske for erhvervet og dets brug af matematik. Man taler om at opgaverne hver især skal være eksemplariske for hvordan matematik kan bruges i erhvervet. | Med udgangspunkt i tømrernes grundforløb, kan man eksempelvis bede elever om at beklæde en facade eller terrasse med forskellige plader og brædder og undersøge materialeforbrug. Her testes elevens evne til at finde praktiske matematiske løsninger. |
| Det verbale | Er kendetegnet ved at eleven selv skal finde og modellere egen løsning af både abstrakte og konkrete matematiske problemer på baggrund af verbalt stillede opgaver. De stillede opgaver skal gerne være eksemplariske for erhvervet og for erhvervets brug af matematikken. Det verbale hjørne bruges også til at afklare motivation, skoleerfaringer og potentialer. | Spørgsmål og opgaver skal, hvis det er muligt, tale ind i elevernes kommende erhverv. Det kan handle om verbalt formulerede konkrete opgaver. Eksempelvis: Kontrollér om vinklen er ret, eller streg grundplanen for huset op. Overvejelser og svar udtrykkes også verbalt, eller eventuelt visuelt. Her testes elevernes evne til at modellere matematiske løsninger gennem samtale. Det kan også handle om spørgsmål og samtale om fx motivation, skoleerfaringer og potentialer. |
| Det skriftlige | Kan være opgaver som eleverne genkender fra tidligere skoleundervisning. Altså opgaver, hvor almene formler og udtryk skal behandles, og som kræver abstraktionsevne af eleven og tester bestemte matematiske færdigheder. Det kan også være andre typer opgaver, gerne med virkelige eksempler fra erhvervet. | Her drejer det sig om matematiske opgaver, som kan være i en virkelighedskontekst eller rent matematiske. Det kan fx være regnestykker med forskellige regnearter og formeludtryk fra skolen, som anvendes i erhvervet og i dens faguddannelser. |
Hvorfor skal test indeholde det praktiske, det skriftlige og det verbale?
Når en test skal give et så dækkende billede som muligt af elevernes faglige forudsætninger, skal eleverne have mulighed for at bruge alle de udtryksformer, de kender. Testning af elevernes matematik bør ikke være baseret på skriftlighed og symbolsk formuleret matematik alene.
Kortlægning skal også indeholde verbalisering og arbejde med praktiske opgaver. Det er vigtigt af mange årsager:
- Mange elever lægger stor vægt på praksiserfaring og på fysisk feedback, der opstår gennem praktisk aktivitet.
- Mange elever har valgt uddannelsen på grund af vægten på praktiske tilgange og som et fravalg af boglige og teoretiske tilgange.
- Mange elever opfatter matematik som et instrumentelt fag.
- Mange elever oplever ikke, at matematik er et værktøj, der hjælper dem i deres uddannelse, men snarere som et nødvendigt onde.
- Mange elever oplever ikke, at matematik giver mening, og har ikke erfaringer med, hvad det vil sige at forstå noget i matematik ud over blot at huske instrumentelle fremgangsmåder.
Hvis skriftlighed og symbolske formuleringer dominerer testen eller kortlægningen, afspejler det ikke elevernes kommende erhverv. I erhvervssammenhæng bruges matematik, ved at man 'oversætter' fra virkelighedens verden og spørgsmål til matematik, arbejder matematisk og derefter 'fortolker' de matematiske svar i virkelighedens verden. Disse (modellerings)processer bør afspejles i testen af eleverne. (Kilde 2 og 3)
Særligt når det drejer sig om at afdække elevernes faglige forudsætninger, er diagnostiske opgaver et godt værktøj. Det er opgaver, der er designet med det formål at afdække elevernes forståelse og mulige misforståelser i forhold til centrale faglige begreber. Også der kan en skriftlig tilgang suppleres med verbale og praktiske tilgange til nærmere afdækning af de enkelte elevernes begrebsforståelse.
Læs også om, hvorfor diagnostiske opgaver er effektive til at afklare forudsætninger
Se eksempler på diagnostiske opgaver
Vis interesse for elevernes forhold til og oplevelser med matematik
Elevers selvforståelse, selvtillid, motivation og ihærdighed er vigtige for læreren at have indblik i som grundlag for at tilrettelægge, gennemføre og evaluere undervisningen. Elevens opfattelser, oplevelser og følelser i forhold til matematik, hvordan matematik bruges, og hvordan det læres, har indflydelse på, hvor meget eleven lærer, hvad eleven lærer, og hvor dybtgående eleven lærer. Når læreren udviser interesse for elevernes indre følelsesliv, skaber det tryghed i klasserummet og bidrager til elevernes deltagelse.
Følgende samtalespørgsmål kan bruges som inspiration ved starten af grundforløbet. De kan bruges samlet, men læreren kan også udvælge nogle af spørgsmålene, eller læreren kan vælge at anvende nogle af samtalespørgsmålene på et senere tidspunkt i grundforløbet.
Spørgsmålene kan anvendes både i mundtlig form ved en samtale med eleverne i klassen eller i mindre grupper. De kan også stilles og besvares skriftligt individuelt, evt. støttet af en gruppesamtale om spørgsmålene, ligesom spørgsmålene kan behandles i forbindelse med praktiske aktiviteter.
Samtalespørgsmål
- Har du lært noget i matematiktimerne i skolen, som du kan bruge?
- Var der lærere i skolen, der gjorde noget godt eller skidt, for at du kunne lære matematik?
- Hvilke dele af matematik i skolen kunne du lide, og hvilke kunne du ikke lide?
- Hvilke dele af matematik i skolen var lette at lære, og hvilke var vanskelige?
- Hvilken måde kunne du bedst lide at arbejde på i matematiktimerne? Alene? Med en makker? I gruppe? …
- Brugte du meget tid på hjemmearbejde i matematik i skolen?
- Har du altid kunnet se og høre, hvad der foregik i matematiktimerne i skolen?
- Har du nogen nu, der kan hjælpe dig med matematik, hvis du får brug for det?
- Glædede du dig til matematiktimerne, eller følte du dig nogen gange dårlig tilpas, når du skulle i gang med en matematiktime?
- Hvad har din omgangskreds og familie sagt om vigtigheden af at lære matematik?
- Følte du dig nogensinde 'udenfor' i matematiktimerne i skolen?
- Følte du, at de matematiklærere, du havde, var gode til at svare på dine spørgsmål og til at høre på, hvad du ville sige?
- Fik du noget ekstraundervisning i matematik i skolen?
- Er det vigtigt for dig at blive bedre, eller god, til matematik?
- Hvad tror du er vigtigst for at være god til at bruge matematik? Medfødte evner? Hårdt arbejde? Lære ting udenad? Eller?
- Kan du godt lide at arbejde med lommeregner, computer, iPad?
- Tror du, at du får brug for at kunne matematik i dit fremtidige arbejde? I din videre uddannelse? I din hverdag?
(Kilde 1)
til: ERHVERVSUDDANNELSER
emne: TEST og KORTLÆGNING
UDGIVET: 2021
Forfattere
Lena Lindenskov
Lektor, ph.d. i matematikdidaktik
Institut for fagdidaktik DPU, Aarhus Universitet/AU
Lauge Sams Granerud
Faglærer
Roskilde Tekniske Skole
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Lena Lindenskov, Pia Beck Tonnesen, Peter Weng (2016). Matematikvanskeligheder på de ældste klassetrin. Dansk Psykologisk Forlag.
- Andersen, M.W., Weng. P. (2019). Dannelse gennem meningsfulde oplevelser med matematik. Dannelse i alle fag. Dafolo.
- Berthold, V. (2019). Matematik for livet. Dannelse i alle fag. Dafolo.