Hvad er teknologiforståelse i matematikundervisningen?
Digitale teknologier har stor og stigende indflydelse på samfundet. Derfor er der i det meste af verden meget fokus på, at eleverne i løbet af deres skoletid udvikler teknologiforståelse. Få et overblik over, hvad teknologiforståelse er, og hvad det har med matematikundervisning at gøre.
Formålet med teknologiforståelse
En arbejdsgruppe har i 2017 beskrevet formålet med at undervise i teknologiforståelse. Ifølge gruppen bør formålet være, at eleverne forstår muligheder og potentielle konsekvenser af digitale teknologier, og at de bliver i stand til konstruktivt og kritisk at deltage i udviklingen af dem. Digitale teknologier kan i den forbindelse være hjemmesider, digitale spil, robotter, interaktive løsninger og datakilder. (Kilde 1)
Teknologiforståelsens 4 områder
Arbejdsgruppen har foreslået 4 elementer til at udgøre indholdet i teknologiforståelse:
Digital myndiggørelse
Den digitale myndiggørelse omhandler elevens forståelse af digitale teknologiers indflydelse på samfundet. Eleven skal blive i stand til at vurdere digitale teknologiers positive og negative konsekvenser samt de muligheder, som en given teknologi åbner op for.
Eksempler
- At diskutere muligheder og problemer ved brug af talegenkendelsesteknologier til fx stemmestyring af fjernsyn og til overvågning.
- At diskutere kryptering af information, som både er med til at sikre privatliv og understøtter kriminel adfærd. Elever på mellemtrinnet kan fx arbejde med et kodehjul og derefter diskutere, hvordan og under hvilke betingelser kodning og kryptering af information er relevant.
Teknologisk handleevne
Den teknologiske handleevne er en kompetence til at håndtere hardware, digitale værktøjer og programmeringssprog. Målet er, at eleverne bliver i stand til at håndtere forskellige digitale teknologier – herunder at programmere, løse tekniske problemer og træffe beslutninger om valg af værktøj til en given opgave.
Eksempler:
- At programmere et spil, der tager input fra tastaturet og omsætter det til, at figurer bevæger sig på skærmen.
- At vælge et relevant matematisk program (fx et regneark eller CAS-program) og bruge det til at løse en udfordring.
Computationel tankegang
Den computationelle tankegang handler om at modellere fænomener med data og beregning, det vil sige at bygge konkrete modeller i et digitalt værktøj eller gennem et programmeringssprog. Eleverne skal lære at afkode forhold fra dagligdagen og fra faglige sammenhænge, samt at oversætte dem til digital form.
Eksempel
- Det kan fx dreje sig om at udvikle en metode til at fordele karameller mellem klassens børn på den årlige karameldag.
Se også modellen over 'Praksis om computationel tankegang' (figur 3) nedenfor.
Digitalt design og designprocesser
Digitalt design og designprocesser omhandler, at eleven kan tilrettelægge og gennemføre iterative designprocesser (det vil sige designprocesser, hvor løsninger løbende afprøves og forbedres) og skabe digitale teknologier til løsning af problemstillinger fra omverdenen. Her sættes fokus på de kreative processer, der indgår i at skabe digitale teknologier.
Eksempel:
- Elever, der udvikler løsningsforslag til teknologisk støttet energibesparelse på skolen gennem intelligent varme og lysstyring. De afprøver deres løsning ved at tænde og slukke for lys og varme som planlagt (fx slukke lyset, når solen skinner) og undersøger, hvordan det påvirker skolens lærere og elever.
Historisk perspektiv på matematik og teknologiforståelse
Seymour Papert var frontløber i det første forsøg på at bruge digitale teknologier til at gentænke matematikundervisningen. Hans hovedidé var at udvikle et børneprogrammeringssprog, hvor elever, med støtte fra lærere, kunne udvikle deres egne matematiske konstruktioner. Dette resulterede i programmeringssproget LOGO, der lader elever konstruere en grafisk figur ved at programmere en lille skildpadde til at bevæge sig rundt på skærmen og afsætte et spor. (Kilde 2)
| 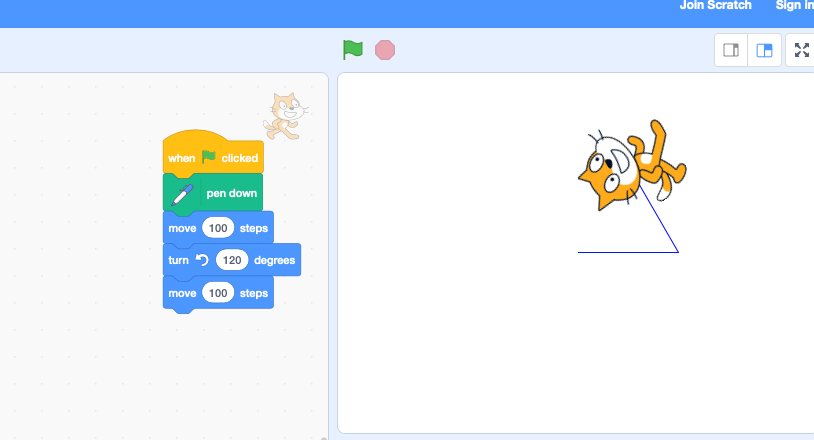 |
| 100 Figur 1. Et eksempel på 'skildpadde-geometri'. Her i programmet Scratch, koden er forklaret i søjlen til venstre. | |
Arbejdet med LOGO udsætter eleverne for en række matematiske udfordringer. Fx skal eleverne gennem kommandoer beskrive den proces – eller algoritme – som skildpadden skal gå igennem for at afsætte en figur. Denne tilgang til geometri blev af Papert og andre døbt 'skildpadde-geometri'. At arbejde med geometri ved hjælp af skildpaddeprogrammering støtter eleverne i at forstå geometriske konstruktioner ud fra skildpaddens perspektiv i modsætning til det 'fugleperspektiv' på geometrien, der dyrkes i euklidisk og kartesisk geometri.
Eksempel: Undervisningssekvens i Skildpadde-geometri
Flotte mønstre i Scratch
Ved at bruge penneværktøjet i Scratch kan eleverne udvikle deres egne mønstre og samtidigt lære at skrive kommandoer, der fører til bestemte handlinger (se figur 1).
Man kan fx:
- udfordre eleverne til at skrive et program, der laver en trekant, et kvadrat eller en anden figur.
- lade eleverne lægge planer for bestemte konstruktioner, fx et hus, der ser ud på en bestemt måde, og så forsøge at skrive et program, der gør det.
- udvikle mønstre med udgangspunkt i simple geometriske figurer som fx et kvadrat. En ofte anvendt idé, der kombinerer fokus på algoritmer med geometrisk forståelse, er at tegne den samme figur igen og igen bare lidt forskudt eller drejet.
| 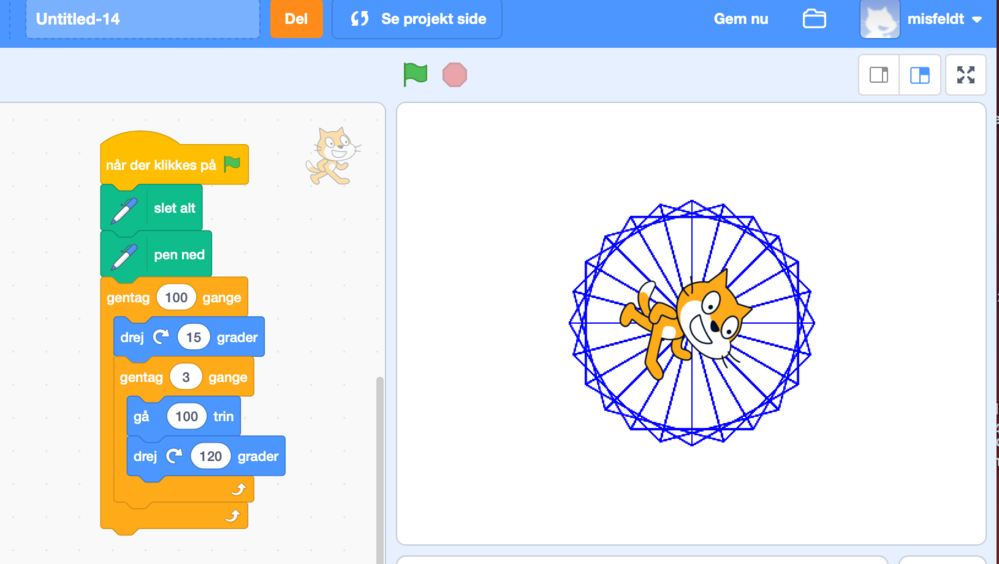 |
| Figur 2. Flotte mønstre i skildpadde-geometri. Her i programmet Scratch, koden er forklaret i søjlen til venstre. | |
Ny bølge med fokus på programmering
Arbejdet med programmering i matematikundervisningen gik af mode over det meste af verden i starten af 1990'erne, men er vendt voldsomt tilbage siden midten af 2010'erne. Der er flere grunde til, at fokus skiftede i starten af 90'erne. Der var implementeringsvanskeligheder omkring LOGO-matematik både på grund af teknologiens modenhed, og dels fordi den tilgang til matematik, som LOGO-matematikken stod for, var meget anderledes end den sædvanlige undervisning. Men det var også i denne periode, at der dukkede en række nye digitale værktøjer op, som på anden vis kunne berige matematikundervisningen.
I den nye bølge af programmering og matematikundervisning er samspillet mellem matematik og teknologiforståelse til dels vendt på hovedet. Frem for at se programmering og digitale teknologier som noget, der skal berige matematikundervisningen, er formålet nu også at udvikle elevernes digitale kompetencer.
Computationel tankegang
Et af de 4 kompetenceområder i teknologiforståelse står helt centralt i forbindelse med, at der igen er blevet fokus på samspillet mellem teknologi og matematik, nemlig computationel tankegang. Jeanette Wing har beskrevet computationel tankegang i 2006, som noget alle bør lære – helt på linje med at læse, regne og skrive, og som tæt knyttet til både problemløsning, algoritmer og abstraktion. (Kilde 3)
For at få hold på, hvad computationel tankegang egentlig betyder for skolens matematiske og naturvidenskabelige fag, har Weintrop og kolleger udviklet en model over, hvad de kalder praksis om computationel tankegang. (Kilde 4)
Model: Praksis om computationel tankegang
Her tales om 4 praksisområder: datapraksisser, modellering og simuleringspraksisser, problemløsnings-praksisser og systemstænknings-praksisser. Denne tilgang til computationel tankegang dækker også over aspekter af det, der kaldes teknologisk handleevne i de danske dokumenter om teknologiforståelse.
| Datapraksis | Modellering og simuleringspraksis | Problemløsningspraksis | Systemtænkningspraksis |
| Samle data | At bruge computermodeller til at forstå et begreb | At klargøre problemer til datalogiske løsninger | Udforske et komplekst system i sin helhed |
| Skabe data | At bruge computermodeller til at finde og teste løsninger | At programmere | forstå relationerne internt i et system |
| Manipulere data | At vurdere computermodeller | At vælge effektive datalogiske værktøjer | Tænke forskellige niveauer |
| Analysere data | At designe computermodeller | At vurdere forskellige tilgange til problemløsning | Kommunikere omkring et system |
| Visualisere data | At udvikle computermodeller | At udvikle modulære løsninger | Definere et system og håndtere kompleksitet |
| At tænke abstrakt i datalogiske sammenhænge | |||
| Debugging |
Figur 3. Computationelle tankegangs praksisser. (Kilde 4, tabel 2)
Samspil mellem matematik, computationel tænkning og teknologiforståelse
Overblikket i figur 3 viser et relativt stort fællesskab med matematisk kompetence, og mange forhold peger på, at der er et vist fællesskab mellem computationel tankegang og matematisk kompetence. Nedenfor er en beskrivelse af sammenhængen og eksempler på de 4 praksisområder:
Datapraksisser
Datapraksisser vedrører elevers håndtering af data og omfatter indsamling, oprettelse, manipulation, analyse og visualisering af data. Disse praksisser trækker i høj grad på statistik og sandsynlighedsregning samt på hjælpemiddelkompetencen.
Eksempel:
- At organisere data i et lille computerspil som eleverne laver, så det er muligt at se, hvem der har scoret flest point i spillet i dag, i denne uge og i det hele taget.
Modellering og simuleringspraksisser
Modellering og simuleringspraksisser trækker på matematisk modelleringskompetence, men adskiller sig også herfra ved at fokusere på at implementere en model i et programmeringssprog frem for på at forstå bestemte matematiske sammenhænge.
Eksempel:
- At modellere en epidemi i et agentbaseret programmeringssprog (som fx NetLogo eller StarLogo), hvor de enkelte agenter programmeres til at blive smittet, hvis de møder en syg, og derefter først bliver syge og så raske igen med en vis sandsynlighed. En sådan simulation, vil kunne køres en række gange (måske med forskellige parameterværdier) og bruges som udgangspunkt for en diskussion af epidemier og samfundets respons herpå.
Problemløsningspraksisser
Problemløsningspraksisser er i fokus for både matematik og teknologiforståelse. Og der er nogle klare overlap imellem matematisk problembehandlingskompetence og den problemløsende del af datalogisk tænkning/computationel tænkning. Der er dog også nogle forskelle. Weintrop fokuserer blandt andet på debugging (at fejlsøge og rette sit program) og programmeringsaktiviteter, som ikke normalt ses som en del af matematikfagligheden. Disse problemløsningspraksisser er ofte præget af, at man skitserer en løsning og forsøger at udvikle de første skridt, hvorefter løsningen rettes til og udvikles videre. Snarere end at forsøge at løse problemet rigtigt første gang, arbejdes der altså med en bevidst iterativ tilgang til problemløsning. Denne tilgang er en fin mulighed for at arbejde med at lære af fejl og se fejl som en naturlig del af en matematisk proces.
Systemtænkningspraksisser
Systemtænkningspraksisser er nok den del af Weintrops model, der ligger længst væk for vores normale forståelse af matematisk kompetence, samtidigt har denne måde at tænke på meget at tilbyde matematikundervisningen. Systemtænkningspraksisser handler om at forstå et komplekst system og forholdet mellem dets dele. Dette minder på mange måder om modellering, men er mere kvalitativt og holistisk. Det vil sige, at fokus ikke udelukkende er på at beslutte, hvilke variable der indgår i modellen og hvordan (det falder under modellering og simuleringspraksisser), men at man samtidigt hermed holder øje med, hvilke andre dynamikker der influerer de forhold, der undersøges.
Eksempel:
- En model over sammenhængen mellem tilladt hastighed og antallet af ulykker på en motorvej vil være afhængig af forhold som trafikmængde og mulige alternative ruter. Systemtænkningspraksisser lægger op til, at man har opmærksomhed på disse sammenhænge, selv om de ikke direkte indgår i den model, man arbejder med.
TIL OVERVEJELSE I FAGTEAMET
- Har I erfaringer med at arbejde med teknologiforståelse i matematik? Hvilke muligheder og udfordringer ser I i samspillet?
- Hvilket ansvar og hvilke muligheder har matematikundervisningen for at bidrage til elevernes teknologiforståelse?
- Kan begrebet computationel tankegang bruges til at udvikle matematikundervisningen i en positiv retning? I givet fald hvordan?
til: GRUNDSKOLE
emne: TEKNOLOGIFORSTÅELSE
UDGIVET: 2021
Forfatter
Morten Misfeldt
Professor
Institut for Naturfagenes Didaktik, KU
Programmeringsværktøjer i matematikundervisningen
Der er en række ressourcer man kan opsøge for at komme i gang med at bruge et programmeringsværktøj i sin matematikundervisning. Gode steder at starte er:
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Fælles mål for forsøgsfaglighed i teknologiforståelse som fag og i matematik. emu.dk/grundskole/teknologiforstaaelse/faghaefte-faelles-maal-laeseplan-og-vejledning?b=t5-t34.
- Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books Forsøgslæseplanen til teknologiforståelse – både matematik og som fag
- Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33-35.
- Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127-147.
Anden litteratur om teknologiforståelse i matematikundervisningen
- Ejsing-Duun, S., & Misfeldt, M. (2016). Programmering af robotenheder i grundskolen. Tidsskriftet Læring og Medier (LOM), 8(14). https://doi.org/10.7146/lom.v8i14.21615
- Svenske moduler:
https://larportalen.skolverket.se/#/modul/0-digitalisering/Grundskola/428_matematikundervisningmeddigitalaverktygII_åk4-6
- Musaeus L. H, Hansen, J. Ø., Damsgaard-Madsen, M., & Nielsen K. (2020) Computational Thinking i gymnasiefag. En modelbaseret didaktik. (1. udg.) Aarhus Universitet. Lokaliseret 23. maj 2021 på https://cctd.au.dk/fileadmin/www.cct.au.dk/cctd.au.dk/PDFs/CT-didaktik2020.pdf - Et par relevante forløb fra fra tekforsøget
Indskolingen:
- https://xn--tekforsget-6cb.dk/wp-content/uploads/2020/08/Rumv%C3%A6sner-3.-kl-Matematik-12-08-20.pdf
- https://xn--tekforsget-6cb.dk/wp-content/uploads/2020/09/Polygoner-1.kl_.-matematik-15.09.20.pdf
Mellemtrinnet:
- https://xn--tekforsget-6cb.dk/wp-content/uploads/2020/06/Banestreger-4.-kl.-Matematik-26-06-2020.pdf
- https://xn--tekforsget-6cb.dk/wp-content/uploads/2020/06/Tryghed-i-n%C3%A6rmilj%C3%B8et-6.-kl-Mat.pdf
Udskolingen:
- https://xn--tekforsget-6cb.dk/wp-content/uploads/2020/06/Statistikker-med-bias-8.kl_.-matematik-26-06-20.pdf
- https://xn--tekforsget-6cb.dk/wp-content/uploads/2020/06/Hvordan-t%C3%A6nker-en-computer-9.-kl-Mat..pdf