Aktiviteter, der trækker på matematik og teknologiforståelse
Se en række undervisningsaktiviteter, der belyser samspillet mellem undervisning i teknologiforståelse og matematik ved at anvende teknologiforståelsesværktøjer og processer til at udvikle matematikundervisning.
Programmeringsværktøjer i matematikundervisningen
Der er en række ressourcer man kan opsøge for at komme i gang med at bruge et programmeringsværktøj i sin matematikundervisning. Gode steder at starte er:
Eksempler
Eksempler på leg med matematiske sammenhænge og begreber gennem programmering:
Matematiske begreber – indskoling/mellemtrin
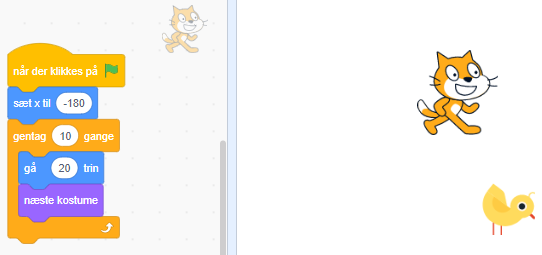
Eksemplet handler om, hvordan elever kan arbejde med matematiske begreber gennem programmering. Brug Scratch til at skabe erfaringer med fx multiplikation som gentagen addition ved at lade to figurer bevæge sig på den samme flade.
A
|
|
B
| 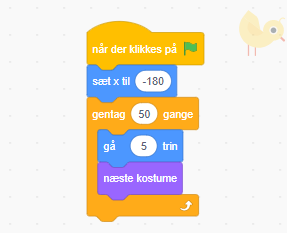 |
| Figur 1. Sammenligning af at gå 20 skridt 10 gange (A) og at gå 5 skridt 50 gange (B). Her i programmet Scratch, koden er forklaret i søjlen til venstre. | |
I dette eksempel er der paralleller til en idé af Ed Dubinsky, der sidst i 1980'erne og op i 90'erne arbejdede med at konkretisere matematiske begreber gennem brug af programmering. (Kilde 1 og 2)
Idéen var at bruge programmering til at skabe en konkret og procesorienteret indgang til abstrakt matematik. Fokus var på gymnasie- og universitetsundervisning, men idéen om at øge elevernes matematiske erfaringsmængde gennem programmering har stadig flere muligheder. Ved at eksperimentere med gentagen addition som i figur 1 kan eleverne få en bedre forståelse af multiplikation.
Statistisk simulering og arealberegning - indskoling/mellemtrin
Problematikken omkring at måle arealet af en figur (i det her tilfælde i NCUM's logo) kan angribes helt anderledes, end vi plejer i matematikundervisningen, med en smule kendskab til programmering og teknologiforståelse.
Ved at kaste 1000 tilfældige punkter ud over en billedfil og så se, om de rammer figuren eller ej, får vi et ret godt mål for, hvor stor en del af billedfeltet, der er dækket af farvet logo, og hvor stor en del, der er hvid baggrund. I nedenstående Scratch-program prøves der simpelthen 1000 gange, og resultatet bliver at omkring 9-10% af billedfeltets areal er dækket af farvet logo.
Programmet starter med at sætte variablen 'tæller' til 0, og gentager derefter 1000 gange proceduren, at:
- gå til en tilfældig billedpixel
- se hvilken farve denne pixel har
- hvis pixlen er grøn, så går tælleren en op, ellers bliver den stående.
Ved mere komplekse billeder (af grene, landkort osv.) er det en rigtig effektiv metode sammenlignet med klassisk opmåling. Programstumpen nedenfor styrer en figur, der er én pixel stor rundt på billedet (der er baggrund).
|
|
| Figur 2. Figurens areal måles gennem stokastisk modellering. Her i programmet Scratch, koden er forklaret i søjlen til venstre. | |
Eksemplet viser, at programmering tilbyder en ny måde at måle arealer på, men det viser også en tilgang til matematisk problemløsning, som aktivt anvender at bruge computerens beregningskraft til at 'prøve en masse gange' for at få svar på et spørgsmål.
Skjult matematik og digital myndiggørelse - udskoling
Skolens eget sociale medie
Eleverne inviteres ind i en designproces, hvor en fiktiv virksomhed, 'Webkompaniet', skal udvikle et socialt medie for skoleelever. Idéen er at lave en pendant til Facebook, Twitter og Instagram, men kun for skoleelever. Alle elever fra 4. klasse og op kan 'poste' beskeder, links og billeder.
Designet er som flere andre sociale medier bygget op om én lang række af indlæg fra andre skoleelever, fra skolens kontor og fra lærerne.

Figur 3. Et nyhedsfeed.
Konsulenten fra Webkompaniet har brug for hjælp til at finde ud af, i hvilken rækkefølge indlæggene skal komme frem for de enkelte elever. Hun forklarer, at der sagtens kan være forskellige rækkefølger for forskellige elever, men at det kan være en idé at starte med at lave et fælles feedet, før man forsøger at tilpasse feeded til den enkeltes præferencer.
Hun har taget information med om, hvordan Facebook løser denne problematik (se nedenfor), og hun har også taget en række eksempler på beskeder med. Eleverne arbejder derefter i grupper med:
- at beskrive, hvad de ønsker sig af feedet. Skal man høre fra sine venner først, kun fra sine venner eller også fra sin klasse og resten af skolen? Hvilken plads i feedet skal beskeder fra skolens kontor og lærere have? Eleverne diskuterer balancen mellem info fra skolen, at feede er interessant, og at mediet bidrager til den sociale sammenhængskraft på skolen.
- at se på de konkrete beskeder, hvordan kan de klassificeres i forhold til de ønsker eleverne har talt om under punkt 1? Hvordan kan beskederne grupperes på en relevant måde?
- at undersøge, hvordan gruppering og rækkefølge kan 'automatiseres'. Hvilke data om beskederne er til rådighed (fx afsender, længde, hvor mange der interagerer med beskeden, typen af ord, der bruges)? Kan disse data bidrage til at afgøre rækkefølgen af beskeder? Kan dette beskrives ved hjælp af en formel eller en algoritme?
- at udarbejde og samle et designforslag, som de fremlægger for Webkompaniet sammen med deres overvejelser i designprocessen. Hvad har de lagt vægt på? Hvad har de været i tvivl om?
Fra et matematisk perspektiv kan undervisningen lægge vægt på oversættelsen mellem konkrete beskeder, principper for rækkefølge, hvilke data der er til rådighed, og hvordan de kan samles i en model.
Elevernes produkter kunne være:
- overvejelser over principper for rækkefølge
- rækkefølgen på de konkrete beskeder
- bud på data om beskeder og regler for automatisk rækkefølge
- et designforslag.
Nedenfor er den beskrivelse af Facebooks algoritme for nyhedsfeed, som konsulenten havde med. (Kilde 3)
Hvordan fungerer Facebook-algoritmen?
- For det første tager Facebook hvert tilgængeligt indlæg i en brugers netværk og scorer disse indlæg i henhold til forudbestemte kategorier, som hvad det handler om, hvor nyt det er, osv.
- Dernæst kasserer algoritmen indlæg, som en bruger sandsynligvis ikke vil engagere sig i, baseret på brugerens tidligere adfærd. Algoritmen fjerner også indhold, som brugerne ikke ønsker at se (dvs. clickbait, misinformation eller indhold, som de har angivet, at de ikke kan lide).
- Derefter kører algoritmen et 'kraftfuldt neuralt netværk' over de relevante indlæg for at score dem på en personlig måde. (For eksempel: Mona er 20 % tilbøjelig til at se vejledningsvideoer fra sin skakgruppe, men vil med 95 % sikkerhed sende en hjertereaktion på et foto af sin søsters nye hvalp). På baggrund heraf arrangeres alle relevante indlæg i en rækkefølge.
- Og endelig udvælger algoritmen en god blanding af medietyper og kilder, så brugeren præsenteres for et interessant udvalg af indlæg.
Spildesign med et programmeringssprog - indskoling/mellemtrin
En aktivitet, der er meget oplagt og anvendt, er design af små computerspil med fx Scratch. Spil er en form for aktivitet, som eleverne kender, og der er mange værktøjer, der kan bruges til at lave spil (se fx figur 4 og 5 for konkrete bud på, hvordan man kan gå igang med at lave spil). Der er en lang række matematiske begreber og fænomener, der byder sig til, når man skal designe spil. Fx er koordinatsystemet meget brugbart, hvis man skal kontrollere figurer i et spil, og tilfældige tal er oftest brugbare, hvis man skal designe uforudsigelig adfærd.
Når man designer spil i Scratch, vil der være en række forskellige aspekter af matematik, der kan bringes i anvendelse. Man kan fx lade en figur bevæge sig enten i forhold til et fast koordinatsystem, i forhold til egen placering og retning (som i skildpadde-geometri) eller relativt til andre figurers placering. Disse muligheder kan give anledning til samtaler og refleksioner af geometrisk karakter.
Der er mange måder at komme i gang med at designe computerspil med sine elever:
- En indgang kan være at skabe en simpel historie, som man prøver at bearbejde til et spil.
- En anden kan være at efterabe nogle klassiske platform-spil (fx Space Invaders eller PacMan).
- En tredje mulighed er at give eleverne nogle spil, der allerede er lavet, som de så kan bygge videre på og forandre.
Kombination af fagligt fokus og kreativitet
Det er erfaringsmæssigt udfordrende at kombinere et fagligt fokus med elevernes kreativitet og idérigdom. Nedenstående spil er et lille eksempel på dette. I eksemplet skal hunden fange tacoen og tage en bid af den. Hunden styres med piletasterne, og den bider af tacoen ved, at man trykker på space. Hvis det lykkes hunden at tage en bid, kvitterer den med et bjæf. Tacoen bevæger sig rundt i rette linjer. Når den rammer kanten af billedet skifter den retning – helt tilfældigt.
Der er to figurer (sprites), der programmeres hver for sig: taco (figur 4) og hund (figur 5).
|
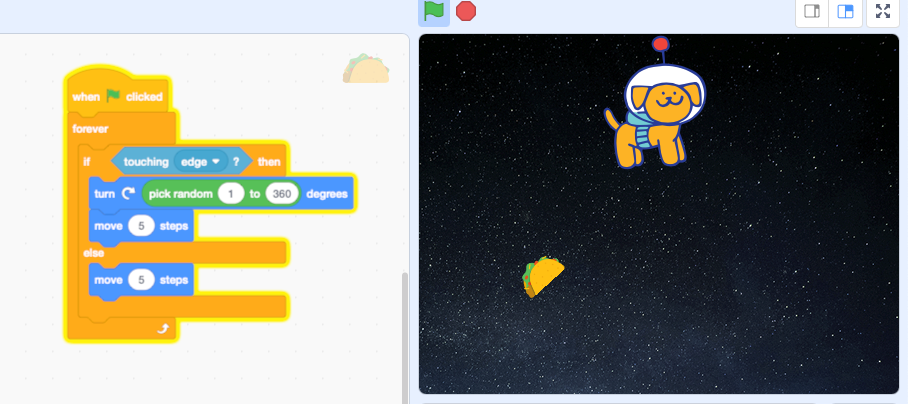
| Figur 4. Tacoens program. Programmet starter, når du klikker på flaget. Programmet kører i en evig løkke. Hvis tacoen rammer kanten, så drejer den til en tilfældig retning og prøver at bevæge sig fremad igen. Eksemplet er fra programmet Scratch. |
|
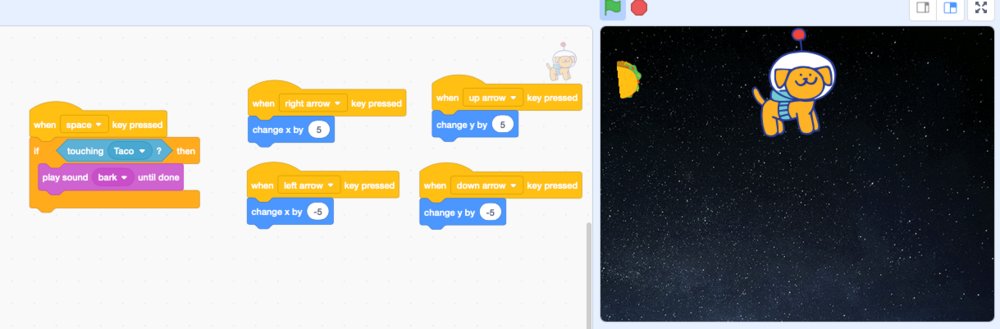
| Figur 5. Hundens program. Hunden styres gennem kendskab til koordinatsystemet (de fire programstumper til venstre), og den bjæffer, hvis man trykker mellemrum, imens den rører taco-spriten. Eksemplet er fra programmet Scratch. |
TIL OVERVEJELSE I FAGTEAMET
Diskutér ét af eksemplerne i teksten. Hvilke matematiske kompetencer, hvilke færdigheder og hvilken viden kan komme i spil?
- Tag udgangspunkt i aktiviteten om skolens sociale medie. Diskutér fænomenet 'skjult matematik'. Hvordan underviser man eleverne i at forholde sig til den matematik, der er skjult i deres digitale omverden?
- Tag udgangspunkt i aktiviteten om at designe små computerspil i Scratch. Overvej og diskutér i teamet hvilke forskellige samtaler man kan have med eleverne, der fokuserer på matematiske begreber eller kompetencer. Tænk gerne på, hvordan aktiviteten kan udvikles, så der kommer flere matematiske begreber i spil.
til: GRUNDSKOLE
emne: TEKNOLOGIFORSTÅELSE
UDGIVET: 2021
Forfatter
Morten Misfeldt
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
Breidenbach, D., Dubinsky, E., Hawks, J., & Nichols, D. (1992). Development of the process conception of function. Educational studies in mathematics, 23(3), 247-285.
- Misfeldt, M (2021). Mellem læringspotentiale og skuffelse – et bud på en it-didaktik for matematik. I Andersen, M. W. & og Weng, P. (Red) Håndbog om matematik i grundskolen, (2. udg) København: Dansk Psykologisk Forlag.
- Cooper, P. (2021, 1. marts).Understanding the Facebook agoriihm and how to make it work for you in 2021. Lokaliseret d. 30. september 2021 på: startupjunkie.org/blog/2021/3/1/understanding-the-facebook-algorithm-and-how-to-make-it-work-for-you-in-2021