Hvad er matematisk modellering og problembehandling?

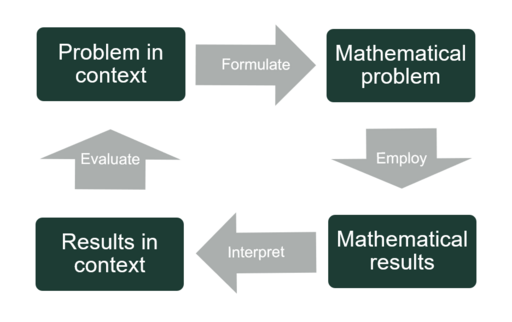
Denne model er meget overordnet og viser de grundlæggende relationer mellem den fysiske virkelighed (til venstre) og den matematiske verden (til højre) (se Figur 2). Den ligger til grund for PISA-undersøgelsen. Kilde 2

Modellen har sin styrke i, at den hurtigt giver et overblik over de overordnede processer i en matematiske modelleringsproces – altså en modelbygningsdel, hvor modellen anvendes til matematisk problemløsning. Pilene går kun i én retning, men til gengæld ser vi, at man kan ”stå på” ved alle hjørner. Starter man f.eks. ved et ”matematisk resultat”, altså et facit på en udregning, både en computerberegning eller håndregning, skal dette resultat fortolkes, og man skal vide, hvad resultatet betyder i den konkrete sammenhæng. Dernæst skal resultatet evalueres ift. denne konkrete sammenhæng. Det kan være enten en praktisk evaluering, hvor man afprøver om f.eks. et bestemt antal kg sand er tilstrækkelig til at lave en god nok cement til en given konstruktion, eller en teoretisk, hvor man konsulterer tabeller el.lign. for at undersøge facits rimelighed. Dette kan enten betyde endestationen til problemløsningen eller, at man er nødt til at formulere et nyt problem, som matematikken skal hjælpe med at løse, da det tidligere resultat ikke udgjorde en god løsning. Den nye matematiske problemstilling vil tage nye forhold i betragtning og dernæst lede til et nyt resultat. Og så er vi tilbage ved udgangspunktet – i dette tilfælde. Som sagt kan man begynde hvor som helst, men processen er modelbygning, så pilene går kun i én retning.

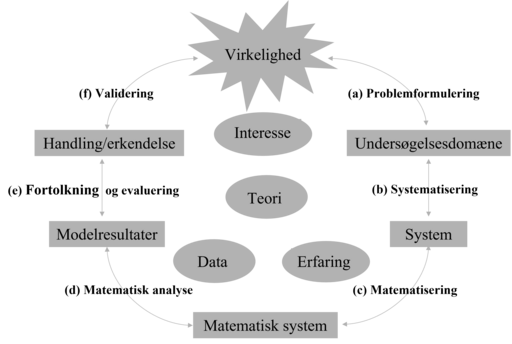
I denne model er der et fokus på, at matematisk modellering starter i en oplevet, kompleks og rodet virkelighed. Kilde 3

Figur 3 viser en modelleringscirkel med særskilte elementer, som er mere detaljerede, end vi så i Figur 2/Model 1. Det primære fokus er her på modelbygningsdelen set i, at bogstaverne (a)-(f) indikerer en retning, selv om pilene dog går i begge retninger mellem hvert deltrin. Det, at pilene peger begge veje, er for at sætte fokus på, at hver af disse trin ikke er en en-gang-for-alle overgang fra et trin i modelleringsprocessen til det næste, men at man naturligt kan gå frem og tilbage ved hvert trin.

Med motivering (a) forstås, at man ud fra den komplekse virkelighed udvælger et udsnit med særlig interesse. Systematisering (b) betyder, at man inden for dette udsnit udvælger særlige karakteristiske træk, som skal indgå i ens model. Matematisering (c) betyder, at disse informationer føres over i den matematiske verden og oversættes til matematisk sprog. I den matematiske analyse (d) anvendes matematisk teori og metoder til at besvare disse spørgsmål. Disse svar skal efterfølgende (e) fortolkes og oversættes tilbage til den virkelige verden. Med procesevaluering (f) menes der, at eftersom matematiske modeller ikke leverer korrekte løsninger, må disse afprøves/testes i den faktiske virkelighed. Dette vil ofte betyde, at dele af modelleringsprocessen gentages for at opnå en bedre model.

Det er vigtigt her at understrege, at modelleringsprocessen i praksis aldrig foregår som en lineær proces, hvor man først går til næste trin, når man er færdig med det første. I praksis går man frem og tilbage mellem trinnene, og processen (a)-(f) er en spiral, hvor man kan tage lige så mange omgange, som det er nødvendigt.

For både elever og undervisere kan modelleringscirklen anvendes som en form for checkliste til at se, om der er dele af processen, man har sprunget over, og her kan den mere detaljerede Model 2 være en større hjælp end Model 1.

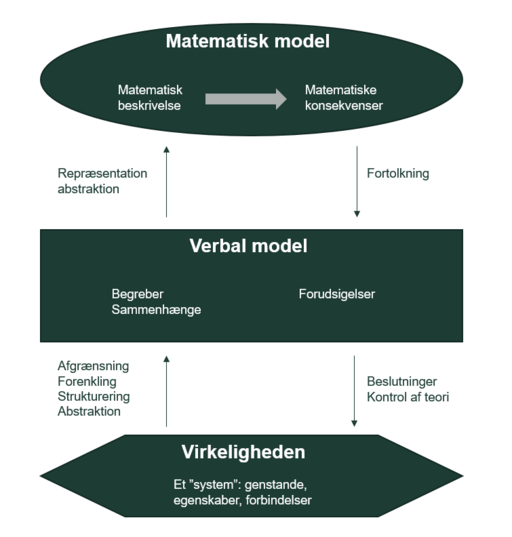
Denne model (Figur 4) for modelleringsprocessen er opstillet af den danske matematiker Ebbe Thue Poulsen. Kilde 4

Processen kan starte to steder. Når den, som i Model 2, starter for neden, er udgangspunktet en ”rodet virkelighed”, også her illustreret med en ikke-regulær figur. Processen er meget lig processen i Model 2, men her er angivet vigtigheden af en ”verbal model”. Den verbale model har visse ligheder med Motiveringsfasen i Model 2, men Model 3 trækker dette trin særligt frem. Den verbale model kan fortolkes til at være en form for problemformulering – hvad er det præcist, man vil modellere (ved pilene til venstre der peget op) – eller (ved pilene til højre, der peger ned) – en formulering af hvad det præcist er, man har fundet ud af sagt på ikke-matematisk sprog.

Poulsens model kan dog også anvendes til Modelanalyse, hvis man starter for oven med en matematisk model, der tolkes til en verbal model, dvs. oversættes til uformelt ikke-matematisk sprog. Dernæst kontrolleres eller afprøves modellen i virkeligheden.

Poulsens model benævner en række centrale faser i en modelleringsproces, som også er en konkret hjælp til den faktiske modelleringsproces, nemlig at overgangen fra virkeligheden til den verbale model indebærer afgrænsning, forenkling, strukturering og abstraktion. Derudfra kan den verbale model formuleres ved at anvende relevante begreber og tidligere etablerede sammenhænge. Ved overgangen til selve den matematiske model, sker der en yderligere abstraktion og repræsentation, og inden for selve den matematiske model sker der først en matematisk beskrivelse, som leder til et matematisk resultat (konsekvenser). Ligeledes med de andre pile.