Praksis – At finde sammenhænge mellem tal
De tidsmæssige rammer
Læringssporet strækker sig fra 2. klasse til 6. klasse. Som beskrevet i afsnittet ’Tilgang’ gentages sporet flere gange.
Et undervisningsforløb på 2-3 uger kan fx bestå af tre gennemløb. Og i perioden mellem 2. og 6. klasse kan et sådant undervisningsforløb fx afvikles en gang om året.
Det faglige udgangspunkt
Det er en forudsætning, at elevernene er i stand til at addere etcifrede og tocifrede tal, og at de er begyndt arbejdet med multiplikation. Især er det en fordel, hvis de kan forbinde multiplikation med gentagen addition.
Igennem læringssporet forudsættes det, at eleverne sideløbende arbejder med alle regningsarter inden for de naurlige tal.
Fase 1
En central del af fase 1 består i at engagere eleverne i en funktionssituation. Det er afgørende, at de kan leve sig ind i, hvad det er for en problemstilling, de skal undersøge, og hvad det præcis er for nogle talpar, de skal finde frem til.
En funktionssituation kan være kompleks, og man kan ikke forvente, at elever på de yngste klassetrin på egen hånd kan læse sig frem til, hvad der er på spil. De vil ofte have brug for at afklare betydninger af figurer eller andre ting, der indgår i situationen, eller afklare, hvilke forventninger der præcis er til dem. Derfor kan det være en god idé at iscenesætte en funktionssituation gennem en fælles samtale i klassen.
Den følgende episode er baseret på et forløb i en 2. klasse, hvor læreren iscenesætter aktiviteten med rektangler, der har en fast sidelængde på 4.
Fase 1
At finde talpar i funktionssituationer med lineære sammenhænge.
Iscenesættelse af rektangler med fast sidelængde
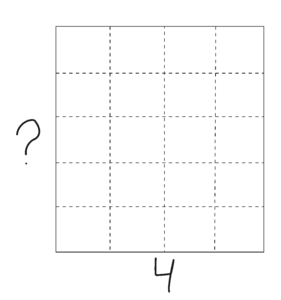
Lærer: I skal arbejde med en opgave, hvor I skal tegne en bestemt slags firkanter på ternet papir. De kan fx se sådan her ud (tegner på tavlen som figuren til højre). De firkanter, I skal tegne, skal – ligesom den her – have siderne lige lange to og to (peger). Og så skal de have hjørner, der ser sådan ud (peger). Er der nogen af jer, der kan få øje på den slags firkanter her inde i vores klasse?
Albert: Ja, døren (peger).
Beate: Også vinduerne (peger).
Cecilie: Og bordene…
Lærer: Enig. Er der nogen af jer, der ved, hvad den slags firkanter hedder?
Tavshed

Lærer: Nej? Man kalder dem for rektangler… Rektangler er de firkanter, der har fire af den slags hjørner.
Der er én ting mere, som skal gælde for de firkanter… eller rektangler, I skal tegne. To af siderne skal være lige præcis 4 lange (viser på tavlen). 1, 2, 3, 4 (skriver 4). Men I må selv bestemme, hvor lange de andre sider skal være (skriver '?').
Kan I se, hvor lange de andre sider er her?
Dicte: 5.
Lærer: Ja. I skal tegne mange rektangler, så måske tegner I nogle, der har en side på 4, og så en side på… 6? Eller måske 10? Eller 1? Eller…
Ella: 100!
Lærer: Ja, måske, hvis I kan få plads, for I skal tegne på sådan nogle papirer her (viser A4-sider med kvadratnet).
OG… Nu kommer noget vigtigt. Hver gang I har tegnet et rektangel, skal I finde ud af, hvor mange tern der er inde i rektanglet. Lad os lige se på det rektangel, jeg har tegnet på tavlen. Er der nogen, som vil hjælpe mig med at finde ud af, hvor mange af de her tern, der er inde i rektanglet? (Peger på et tern).
Frederikke: Må jeg komme op og tælle dem?
Lærer: Ja, men vent lidt. Jeg vil lige høre, om der er nogen, som har andre idéer end at tælle.
Beate: Der er 20.
Lærer: 20? Hvordan fandt du ud af det?
Beate: Altså, der er 5 og 5, det er 10. Så 5 mere, det er 15. Så 5 mere, det er 20.
Lærer: (Til Frederikke) Vil du nu prøve at tælle og se, om du er enig?
Senere forklarer læreren, at eleverne skal arbejde to sammen i 15 minutter med at tegne rektangler med en valgfri sidelængde og en sidelængde på 4. I hvert rektangel skal de finde det samlede antal tern. En elev spørger, om det er lige meget, hvilken ’vej’ de tegner rektanglerne: 'Må de 4 godt være ude i siden?'. Læreren bekræfter dette.
Mens eleverne arbejder, lægger læreren mærke til, hvordan de finder det samlede antal tern. De fleste tæller, men læreren opfordrer eleverne til at skyde ’genveje’. Nogle elever begynder at bruge gentagen addition eller udnytte gangetabeller, de kender. Nogle finder fx antallet af tern i et rektangel med den frie sidelængde 10 ved at regne 10 + 10 + 10 + 10. Andre tænker 4, 8, 12, 16, …, 40. Få siger, at de ganger, fx 4⋅10=40.
Iscenesættelser på senere klassetrin i læringssporet har de samme karakteristika som eksemplet. Læreren inddrager eleverne i funktionssituationen og problemstillingen gennem en fælles samtale. Undervejs afklares begreber og forventninger.
I funktionssituationer, der vedrører en omverdensituation, kan det være en idé at inddrage eleverne ved at knytte en fortælling til situation. Opgaven med borde og stole (se afsnittet Tilgang) kan fx iscenesættes med en fortælling om bordopstilling til en (have-)fest.
Fase 2 og 3
I fase 2 er det hensigten at tydeliggøre elevernes arbejde i fase 1 med to forskellige redskaber: Funktionstabeller og regneudtryk. I fase 3 er det hensigten, at eleverne opdager, begrunder og beskriver generelle lineære sammenhænge faktuelt og kontekstuelt. I praksis kan de to faser let komme til at flette sammen. Derfor beskrives de samlet i det følgende.
I første omgang kan funktionstabeller bruges fælles i klassen til at samle de talpar, eleverne har fundet frem til i fase 1. I aktiviteterne med rektanglerne og med borde og stole kan begyndelsen af tabellerne fx komme til at se sådan ud:

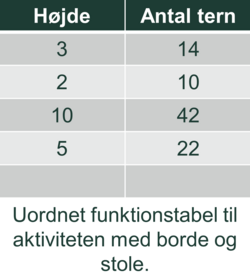
Arbejdet kan organiseres, så hvert makkerpar fortæller om et af deres talpar. Det hører med, at de forklarer, hvordan de har fundet antallet af tern. Deres forklaringer kan understøttes med tegninger på tavlen. Hvis makkerparret, der har fundet talparret 10 og 40 fortæller, at de er nået frem til 40 ved at bruge 4-tabellen, kan de (eller læreren) fx vise, hvordan 4-tabellen passer med tegningen. De øvrige elevers opgave er i denne forbindelse at vurdere, om de resultater, forskellige makkerpar har fundet, ser ud til at være rigtige.
Efterfølgende kan klassen, evt. i fællesskab, fremstille ordnede tabeller (lad de uordnede tabeller blive på en fælles tavle). Begyndelsen af de ordnede tabeller kan komme til at se sådan ud:
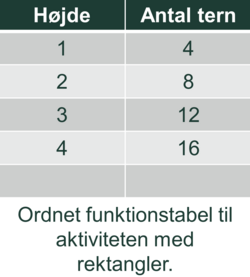

De ordnede tabeller giver eleverne mulighed for at opdage den rekursive sammenhæng og samvariationen mellem tallene (se Tilgang). I begge tabeller herover kan de fx opdage det mønster, at tallene i højre side vokser med 4 fra række til række – eller i et samvariationsperspektiv: Hver gang tallene i venstre side vokser med 1, vokser tallene i højre side med 4. Elever formulerer typisk sådan en opdagelse med vendinger som ’Den vokser med 4 hele tiden’, eller ’Det er 4-tabellen’ eller ’Det er tallene midt imellem tallene i 4-tabellen’. Med lærerens støtte kan de bruge deres erfaringer fra fase 1 til at argumentere for, at denne opdagelse gælder generelt, fx ’Det passer med, at hver gang man gør højden 1 større, så kommer der 4 tern mere’ eller ’Hver gang man sætter 1 bord mere på, så kan der være 4 stole mere’.
For at fokusere på korrespondancesammenhængen kan det være en idé at vende tilbage til den uordnede tabel og supplere med regneudtryk. Umiddelbart kan det være vanskeligt at se mønstre i denne tabel, men som beskrevet i det forrige kan eleverne beskrive, hvordan de fandt frem til deres talpar. Nogle af disse forklaringer kan læreren beskrive med regneudtryk.
Fase 2
At beskrive lineære sammenhænge med funktionstabeller og regneudtryk.
Fase 3
At opdage, begrunde og beskrive generelle lineære sammenhænge faktuelt og kontekstuelt.
Korrespondancesammenhæng i rektangler med fast sidelængde
Et makkerpar fortæller, at de har fundet talparret 5 og 20 ved at regne ’5 plus 5 plus 5 plus 5’. På den baggrund skriver læreren regneudtrykket '5 + 5 + 5 + 5' på tavlen, og klassen diskuterer, hvorfor man kan regne på denne måde. ’Det er fordi, der er 5 der og 5 der og 5 der og 5 der (peger på de lodrette kolonner i rektanglet)’. Andre elever siger, at man lige så godt kunne skrive 4 gange 5, for ’4 gange tager man 5’. Læreren skriver begge udtryk og spørger, om man kan tænke på samme måde, hvis sidelængden er 10. Efterhånden kommer der til at stå en række regneudtryk med ensartet struktur på tavlen:

På den måde får eleverne mulighed for at bruge mønstrene i regneudtrykkene til at opdage og beskrive den generelle korrespondancesammenhæng. Det kan meget vel være med faktuelle generaliseringer som ’Hvis højden var 50, ville det være 50 + 50 + 50 + 50 eller 4 $\cdot$ 50’. Begrundelser for denne generalisering kan de bygge på deres arbejde i fase 1, fx ’Der er altid 4 rækker med lige så mange tern, som højden er’.
Læreren kan støtte elever til at foretage kontekstuelle generaliseringer ved at bede dem forklare det for en udenforstående person: ’Hvordan vil I forklare jeres forældre, hvordan de altid kan finde antallet af tern i sådan et rektangel?’. Fra en elev i 3. klasse kan forklaringen lyde: ’Jeg vil sige, at de skal tælle, hvor høj den er. Det tal skal de plusse med sig selv fire gange’.
Arbejdet i fase 2 og 3 er helt parallelt i andre aktiviteter, men strukturen i regneudtrykkene bliver vanskeligere i lineære sammenhænge, der ikke er proportionale, og det er mere udfordrende at se mønstre i sådanne sammenhænge. Regneudtrykkene i aktiviteten med borde og stole kan fx komme til at se sådan ud:
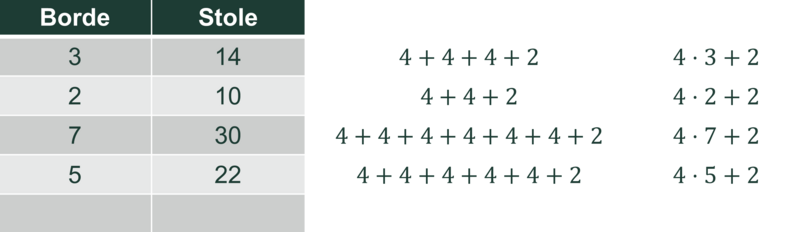
Fase 4
Denne fase handler om at udvide de måder, eleverne beskriver generelle lineære sammenhænge, så beskrivelserne kommer til at omfatte algebraisk notation. Eleverne kan være klar til en sådan udvidelse efter et par gennemløb, som har omfattet fase 1, 2 og 3 i læringssporet.
Brugen af bogstaver i matematik virker for mange elever som et brud med den betydning, de hidtil har lagt i dem. I 4. eller 5. klasse er de jo vant til at forbinde bogstaver med lyde, der kan sættes sammen til ord. At bogstaver også kan symbolisere varierende tal kan derfor forekomme dem unaturligt.
Læreren må eksplicit introducere brugen af bogstaver i matematik. Samtidig er det vigtigt, at eleverne får rige muligheder for med egne ræsonnementer at skabe (ny) mening i dem. Det følgende eksempel viser, hvordan den eksplicitte introduktion kan foregå i forbindelse med aktiviteten med rektangler. Det er en forudsætning, at eleverne i klassen kan formulere eller følge faktuelle og kontekstuelle generaliseringer af sammenhængen mellem den frie højde og antallet af tern i et rektangel.
Fase 4
At opdage, begrunde og beskrive generelle lineære sammenhænge på alsidige måder, bl.a. med bogstavudtryk.
Algebraisk notation i rektangler med fast sidelængde
Lærer: Nu har vi set, at hvis den frie side er 5, så kan man finde antal tern ved at regne $4 \cdot 5$ (skriver). Vi har også set, at hvis den frie side er 10, så kan vi regne $4 \cdot 10$ (skriver) for at finde antallet af tern. Hvis den er 100, kan vi regne $4 \cdot 100$ (skriver).
Jeg skal vise jer et udtryk, man kan bruge i matematik til at finde antallet af tern, når bare man ved, hvor lang den frie side er.
(Skriver: $4 \cdot h$)
Der står 4 gange h. Man kan faktisk også bruge bogstaver i matematik, men bogstaver betyder noget helt andet, end når I læser i dansk. Hvis jeg nu fortæller jer, at I kan brug $4 \cdot h$ til at finde andet af tern, kan I så sige mig, hvad det h må betyde?
Albert: Det må være højden af firkanten… h må betyde højde. Det begynder også med h.
Bente: 4 gange højde. Det giver altså ingen mening. Man kan ikke gange højde… man kan kun gange tal.
Lærer: Ja, det kan der være noget om. Hvad siger I andre?
Cecilie: Altså højden er jo også på en måde et tal… højden kan være 5 eller 10 eller…
Albert: Det er, hvor lang højden er… eller bare hvor lang den der side er.
Pointen i eksemplet er, at eleverne – ud fra den præmis at et bogstavudtryk i matematik kan bruges i beregninger – får mulighed for at skabe mening i betydningen af bogstavet, når de forbinder det med deres tidligere erfaringer fra funktionssituationen. Samtalen kan fx fortsætte med, at klassen reflekterer over, hvilke tal h kan ’være’. Det virker oplagt, at h kan være fx 1, 2, 3, … 10. Men kan det også være 0? Kan det være 1000? Uendelig stort? Kan det være $\frac{1}{2}$? Kan det være -1?
Det er også vigtigt, at eleverne får mulighed for at forbinde bogstavet med deres arbejde i de forrige faser. Hvor kan man 'se' h'et i regneudtrykkene? I tabellerne? På tegningerne af rektanglerne?
Når eleverne er begyndt er skabe mening i brugen af bogstaver som variable, kan de få til opgave selv at opstille bogstavudtryk i funktionssituationer. En opfølgning til opgaven med rektangler, der har en fastsidelængde på 4, kan være en helt parallel aktivitet, hvor den faste sidelængde bare er 3 eller 5. Skridtet til den nye aktivitet er så lille, at det er realistisk, at nogle elever på egen hånd kan opstille et bogstavudtryk, der beskriver den lineære sammenhæng mellem den frie sidelængde og arealet. Næste opgave kan evt. være sammenhængen mellem den frie sidelængde og rektanglets omkreds. Senere kan eleverne udfordres med at opstille bogstavudtryk i forbindelse med lineære sammenhænge, der ikke er ligefrem proportionale, fx som i aktiviteten med borde og stole.
Det vil næppe være alle eleverne, der på samme tid er klar til at opstille bogstavudtryk, som beskriver lineære sammenhænge. Bl.a. derfor er det vigtigt at holde fast i de faktuelle og kontekstuelle generaliseringer (fase 3). Når klassen på den måde har flere sprog til at udtrykke generelle sammenhænge, giver det desuden rige muligheder for at sammenligne de forskellige måder at udtrykke sig på og på den måde skabe mening i det nye – den algebraiske notation med bogstaver.