At finde sammenhænge mellem tal
Introduktion
Dette læringsspor retter sig mod elevers udvikling af algebraisk tænkning og er tænkt til 2.-6. klassetrin. Set i forhold til stofområdet ’tal og algebra’ i grundskolen vedrører det primært tidlig algebra (som vist på Figur 1 herunder).
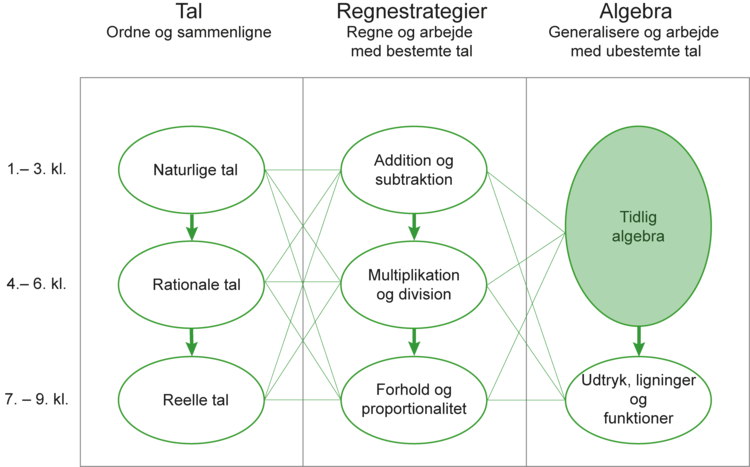
Læringsspor til grundskolen udviklet af NCUM under den fælles indsats for tal og algebra.
Udgivet 2025
Forfattere på læringsssporet er Thomas Kaas, Charlotte Krog Skott, Morten Blomhøj og Marit Hvalsøe Schou.
Mål
Læringssporet skal bidrage til, at eleverne bliver i stand til generalisere lineære sammenhænge. Det medfører, at eleverne kan opdage, begrunde og beskrive lineære sammenhænge på formen $f(n) = a \cdot n + b$, hvor både $a$, $n$ og $b$ er naturlige tal.
På slutningen af 2. klassetrin kan det fx dreje sig om at opdage, begrunde og beskrive den generelle sammenhæng mellem et antal elever og det antal fingre, de har tilsammen. Elever, der er kommet langt i forhold til målet, kan opdage, begrunde og beskrive en sådan sammenhæng mundtligt og i hverdagssprog, fx med udtryk som: ’Man kan se, hvor mange børn der er, så ved man, hvor mange gange man skal lægge 10 sammen’.
At generalisere betyder i denne forbindelse: at bevæge sig fra specifikke eksempler til at opdage, begrunde og beskrive sammenhænge, der holder på tværs af eksemplerne (Stephens et al., 2017).
På 6. klassetrin kan det fx dreje sig om at opdage, begrunde og beskrive den generelle sammenhæng mellem antallet af centicubes og overfladearealet i ’centicubestænger’ (se Figur 2). Elever, der er kommet langt i forhold til målet, kan opdage, begrunde og beskrive en sådan sammenhæng mundtligt, med tabeller, grafer og algebraisk notation, der dog ikke nødvendigvis har form som en funktionsforskrift. Formen kan fx være
$a = 4 \cdot c + 2$, hvor $a$ er overfladearealet, og $c$ er antal centicubes.
Det er ikke en del af målet, at eleverne lærer fagord som ’lineære sammenhænge’ og ’at generalisere’. På de yngste klassetrin kan ’lineære sammenhænge’ fx omtales som ’sammenhænge’. Klassen kan tale om generaliseringer som måder, beregninger eller ’opskrifter’, man kan bruge ’hver gang’.
