Eksempel: Definitioner og regneregler for vektorer
Hvor langt kan elever arbejde sig ind i et nyt fagligt emne med et godt problem og en rig kontekst? Det er et spørgsmål, som en gruppe HTX-lærere undersøgte på et efteruddannelseskursus om undersøgelsesbaseret matematikundervisning. Eleverne fik en introduktion til vektorregning og anvendte og udviklede flere regneregler.
På efteruddannelseskurset blev undersøgelsesbaseret matematikundervisning koblet til de nye læreplaner, der angav, at der skulle undervises tidligere i vektorer end hidtil. (Kilde 1)
Introduktionen til vektorregning kan have en tendens til at blive en liste af definitioner og regneregler, der skal præsenteres og trænes, inden man for alvor kommer i gang med emnet. Dette ville lærerne gerne undgå med nedenstående undervisningsdesign.
Undersøgelsesbaseret forløb om definitioner og regneregler for vektorer
I denne undervisning var alle hjælpemidler tilladt. Selve problemet, eleverne skulle arbejde med, var lagt ind i en GeoGebra-fil, der blev delt med eleverne. I filen havde lærerne lagt et ældre kort over det Caribiske Hav, markeret de fire relevante byer som punkter samt kreeret en ny funktion i GeoGebra, der hedder 'vektor fra begyndelsespunkt'. Denne skulle sikre, at eleverne ikke blev frustrerede eller forvirrede over, at programmet tegner vektorerne ud fra origo. Læreren forklarede eleverne, at funktionen var der, men krævede ikke, at eleverne brugte funktionen.
Det var et krav, at eleverne skulle bruge vektorbegrebet i deres besvarelser, selv om de ikke tidligere havde arbejdet med det. Alle elever fik desuden udleveret en kompasrose kopieret på et stykke papir, og de havde adgang til ca. 10-siders lærebogs-materiale om vektorer som pdf-fil samt en kort vejledning til vektorer i GeoGebra.
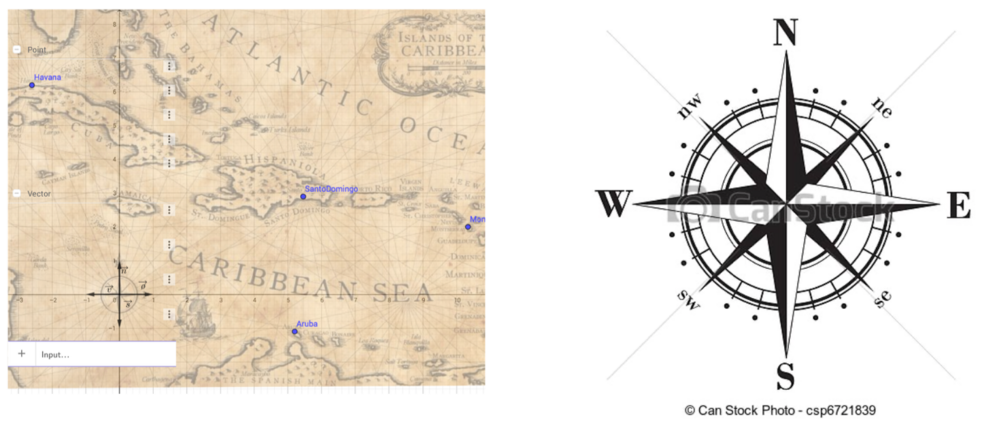
Figur 1: Figuren viser dels et billede af GeoGebrafilen med landkortet over det Caribiske Hav, med angivelse af de nævnte byer og til højre vises kompasrosen.
Problemet, som eleverne fik udleveret:
Du er kaptajn i sørøveriets velmagtsdage og skal føre dit skib fra Havana til Santo Domingo (se vedlagte kort). Din besætning består af et sammenrend af landkrabber, lykkeriddere og letmatroser, som lige akkurat formår at følge en udstukket kurs på formen:
- Sejl 20 sømil mod syd (S), derefter 30 sømil mod sydøst (SØ), derefter 100 sømil mod nordvest (NV), etc.
For noget tid siden sejlede du fra Aruba til Montserrat på 3 døgn, og du regner med at kunne holde samme gennemsnitsfart under denne tur.- Hvilke ordrer skal du give til din besætning for at komme frem, og hvor lang tid vil det cirka tage?
- I forventes at anvende vektorer i jeres besvarelse af spørgsmålene.
Eleverne arbejdede med problemet i 2 gange 60 min. i deres vanlige arbejdsgrupper. To gange undervejs præsenterede hver gruppe, hvor langt de var kommet. De fremlagde ved at koble deres computere til undervisningslokalets videokanon og vise deres arbejde i GeoGebra. Lærerne optog gruppernes fremlæggelser til efteruddannelseskurset, hvor de blev brugt til diskussion af læringsudbyttet: Hvilke elever lærte hvad fra denne undervisning?
Vi viser her, hvordan elevernes undersøgende arbejde har understøttet deres læring af sum af vektorer og længde heraf, som er basale og essentielle elementer i vektorregning.
Enkelte elever spurgte ind til, om de skulle sejle en bestemt vej rundt, og hvad lærerne forventede af dem i den åbne situation. Det er almindeligt, når man stiller åbne opgaver, at eleverne efterspørger en yderligere specificering af problemet, da de er vant til mere lukkede opgaver. Der er imidlertid læring vundet ved, at lade problemet stå åbent, når det er skabt til en passende og afgrænset kontekst som her. Og det er faktisk en kvalitet ved oplægget, at det giver anledning til spørgsmål fra eleverne. Eleverne får brug for at tale med hinanden om problemet, og det støtter, at de tager problemet til sig.
Hvad gjorde eleverne?
Eleverne startede med at få skabt den optimale rute. Det gjorde de ved at markere den med faste eller flytbare punkter, der blev forbundet med linjestykker i GeoGebra. For at sikre fleksibilitet valgte mange de flytbare punkter. Herefter forsøgte de at finde længden af alle linjestykkerne for at kunne afgøre afstanden og dermed tiden det ville tage at sejle fra Havanna til Santo Domingo, når de kendte den tid det tog at sejle fra Aruba til Montserrat.
Det gav imidlertid anledning til noget besvær, og eleverne var stadig ikke kommet tættere på, hvordan linjestykkerne kunne omsættes til en ordre til skibets besætning. Deres første tilgang til dette var at konstruere linjer parallelt med x- og y-akse, hvor der kunne måles vinkler i forhold til. Herefter blev de flytbare punkter trukket i således, at vinklerne kunne passe med retningsangivelsen i kompasrosen.
Disse manøvrer var dog så tunge, at eleverne blev nysgerrige på vektorbegrebet, nogle slog det op i lærebogen, men de fleste ’googlede’ efter definitioner og fandt relevante definitioner på både den algebraiske og den geometriske repræsentation. Herefter gik de tilbage og eksperimenterede med at lave vektorer i GeoGebra. Nogle elever fokuserede på at lave deres egne, hvor de satte vektorer til at have en given vinkel i forhold til den positive del af x-aksen. Andre undersøgte, hvordan lærerens ’vektor fra begyndelsespunkt’-funktion kunne bruges.
Én gruppe valgte at lave en kompasrose i GeoGebra som hjælp til at lave den korrekte ’længde og vinkel’-indtastning.
De definerede derfor deres vektorer som:
øst-vektoren var $\overrightarrow{v_{Ø}} = \left(\begin{array}{c}1 \\0 \\\end{array} \right)$,
øst-nord-øst-vektoren var, $\overrightarrow{v_{ØNØ}}=\left(\begin{array}{c}1 \\\frac{1}{2} \\\end{array} \right) $,
nord-øst-vektoren var $\overrightarrow{v_{NØ}}=\left(\begin{array}{c}1 \\1 \\\end{array} \right) $
og så fremdeles.
Dette gav anledning til figur 2:
Figur 2: Elevernes første bud på en kompasrose i koordinatsystemet
Når de havde defineret disse vektorer, kunne de blot lægge dem i forlængelse af hinanden, tælle antallet og dermed finde længden af ruten. De havde indset af deres retningsvektorer ikke var lige lange, hvorfor deres beskrivelse af ruten blev på formen: $c_1 \cdot \overrightarrow{v_1} + c_2 \cdot \overrightarrow{v_2} + \cdots + c_n \cdot \overrightarrow{v_n}$, hvor $\overrightarrow{v_i}$ er den $i$’te af de definerede vektorer og $c$i$∈$$\mathbb{N}$ er antallet af gange, den $i$’te vektor indgår i ruten. Elevernes beskrivelse var dog med tal og ikke så generisk som her.
Nogle elever var i deres undersøgende arbejde stødt på begrebet enhedsvektor, hvilket de dog ikke var dykket yderligere ned i. Under en gruppes fremlæggelse af ovenstående strategi spørger læreren, hvad man kan kalde deres vektorer. Eleverne gætter på, at han fisker efter enhedsvektorbegrebet, uden de dog kan forklare det. Læreren spørger ud i plenum, om der er andre, der har hæftet sig ved, hvad det dækker over. En elev fra en anden gruppe siger, at disse vektorer har længden 1, hvilket ikke er opfyldt her. Gruppen indser, at de er nødt til at justere, deres kompasrose i GeoGebra. De indser altså, at fx vektoren:
$\overrightarrow{v_{ØNØ}}=\left( \begin{array}{c}1 \\\frac{1}{2} \\\end{array} \right)$,
ikke har den rette vinkel, og de går derfor tilbage og søger mere information om vektorer i lærebogen og på nettet. Dette fører dem til at genbesøge enhedscirklen, definitionen af sinus og cosinus i retvinklede trekaner, hvilket de kobler til definitionen af en stedvektor på enhedscirklen:
$\overrightarrow{u}=\left( \begin{array}{c}\cos ( \varphi ) \\\sin ( \varphi ) \\\end{array} \right) $,
hvor $φ$ er vinklen mellem den positive del af x-aksen og vektoren. De indser, at de kan bruge dette til at bestemme enhedsvektorerne for de ønskede kompasretninger således, at de kan give de nødvendige ordrer til mandskabet på skibet. Ved anden fremlæggelse kan man desuden se, at de ligeledes indser, at det at addere en retnings- eller enhedsvektor flere gange svarer til at multiplicere med en skalar.
Det vil sige, at deres internetsøgning efter definitioner af vektorbegrebet ledte dem til at undersøge vektorer som objekt i deres it-værktøj, hvilket både inkluderede at forstå programmets syntaks, men også relationen mellem syntaks og den grafiske repræsentation, programmet viste. Det kan på en måde siges at være en unødig hindring sammenholdt med, hvis opgaven alene var lavet med papir og blyant. Omvendt kom udfordringerne med at få indtastet netop de vektorer, som eleverne ønskede til at understrege og tydeliggøre betydningen af definitionen af en vektor som en længde og en retning. Selv om eleverne efterhånden kunne bruge GeoGebra til at tegne vektorer på landkortet, der relaterede til forståelige navigationsordre for søfolk, var de stadig famlende over for længden af ruten.
Undervejs i det undersøgende arbejde finder eleverne programmets kommando for at beregne længden af en vektor, hvilket er intuitivt klart, når de er vandrette eller lodrette, men eleverne på dette A-niveauhold accepterer tilsyneladende også uden videre, at længden af de øvrige kan beregnes som hypotenusen i en retvinklet trekant.
En gruppe vælger at definere en vektor, der er summen af rutens vektorer for at finde den samlede længde af ruten: $ \overrightarrow {v_ {samlet }} = c_1 \cdot \overrightarrow{u_1} + c_2 \cdot \overrightarrow{u_2} + \cdots + c_n \cdot \overrightarrow{u}$. Programmet tegner vektoren, og de præsenterer, at GeoGebra viser, at summen af vektorerne er lig fugleflugtslinjen mellem de to byer. Det undrer de sig ikke over, før de beregner længden af ruten, hvor de først kommer til at konkludere, at den snørklede rute er lige så lang som fugleflugtslinjen. Eleverne begynder at mumle og indser at:
$ |\overrightarrow {v _ {samlet }}| ≠ c_1 \cdot |\overrightarrow{u_1}| + c_2 \cdot |\overrightarrow{u_2}| + \cdots + c_n \cdot |\overrightarrow{u}|$.
Lærerne samler op på, hvordan eleverne nu kan formulere forskellige definitioner for vektorer, hvordan man kan beregne længden, at man kan lægge vektorer sammen og trække dem fra hinanden samt finde længde, hvor de nu også ved, at længden af summen af givne vektorer ikke nødvendigvis er det samme som summen af længden af vektorerne. Efter timen, på vej ud ad døren, talte eleverne om, hvordan de havde udviklet nogle regneregler for det nye vektorbegreb. De følte at de kunne addere dem, men da addition med længderne havde overrasket dem, diskuterede de om der mon fandtes særlige regler for multiplikation med vektorer? På denne måde havde timen skabt et godt udgangspunkt for de efterfølgende lektioner, da eleverne allerede gerne ville vide mere.
LÆRINGSUDBYTTE
Da vi på efteruddannelseskurset evaluerede læringsudbyttet af denne undersøgelsesbaserede introduktion til vektorregning, var der bred enighed om, at eleverne var nået langt i deres arbejde med forskellige definitioner samt havde brugt eller udviklet flere regneregler, hvilket viste righoldigheden af problemet og den kontekst, eleverne fik lov at arbejde med den i.
Kan det løses uden computer?
Omvendt var der også en udbredt tvivl om, i hvilket omfang eleverne kunne lægge vektorer sammen, finde længder, indtegne vektorer i et koordinatsystem osv., hvis de alene havde papir og blyant til rådighed. Næppe alle elever ville klare dette problemfrit, men pointen her er, at computeren og den særlige fil blev en rig kontekst, hvor eleverne på kort tid kunne udvikle deres begrebsverden til at inkludere vektorer, regne med dem og indse pointer omkring deres længder. Eleverne havde altså udviklet et ejerskab til dette indhold og erfaringer, der kunne bygges videre på, når de skiftede til at arbejde med emnet på papir og med blyant.
Autonomi og ægte nysgerrighed
Hvad der yderligere er værd at bemærke ved elevfremlæggelserne er, at de i højere grad bliver samtaler om, hvad grupperne præsenterede. For de fleste grupper sagde alle medlemmer noget og var tydeligvis med på, hvad gruppen havde undret sig over og undersøgt ved at referere til gruppesamtalerne, materialer de havde fundet online, i lærebogen eller hvad de havde gjort i GeoGebra, og hvad programmet havde givet dem igen. Problemet og konteksten havde altså givet en autonomi og ægte nysgerrighed, der drev alle til aktiv deltagelse i det undersøgende arbejde.
Orkestrering af klassen
Læreren spillede en relativt tilbagetrukket rolle, der orkestrerede fremlæggelserne fra de mest basale først til de mere avancerede til sidst – selv om de på mange måder mindede om hinanden. Hvis ikke andre elever efterspurgte uddybninger eller stillede spørgsmål, så gjorde læreren det for at sikre sig, at gruppernes tanker stod tydeligt frem efter deres fremlæggelser. Ved anden fremlæggelse kunne man således se, at nogle grupper havde forkastet deres egne første strategier og skiftet til smartere måder som fx fra flytbare punkter og linjestykker til vektorer.
til: GYMNASIER - HTX
emne: UNDERSØGELSESBASERET MATEMATIKUNDERVISNING
UDGIVET: 2021
Forfattere
Britta Eyrich Jessen
Adjunkt
Institut for Naturfagenes Didaktik, KU
Jacob Borby
H.C. Ørsted Gymnasiet, Ballerup
Jonas Kromann
H.C. Ørsted Gymnasiet, Valby
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Jessen, B. E. (2018). Hvordan kan matematiklærere udvikle deres undervisningspraksis? LMFK-bladet, 2, s. 15-21.