Undervisning i multiplikation af etcifrede tal
Det er svært for mange elever at lære at multiplicere etcifrede tal, hvis undervisningen alene baserer sig på udenadslære. Men hvis undervisningen sigter på at kombinere simple multiplikationer med mønstergenkendelse og tænkestrategier, kan eleverne ud over at lære at multiplicere etcifrede tal også udvikle deres talforståelse og forståelse af regningsarternes egenskaber. Læs om, hvordan elever udvikler forståelse for multiplikation og multiplikativ tænkning, og se eksempler på undervisning i tænkestrategier med multiplikation.
Traditionelt har målet for undervisningen i etcifret multiplikation været, at eleverne skulle lære ’den lille tabel’ udenad ved hjælp af træning. (Kilde 3)
Det har imidlertid vist sig, at det er særdeles svært for en stor del af eleverne at lære at multiplicere etcifrede tal, hvis denne kunnen alene er baseret på udenadslære. (Kilde 2)
En række forskere foreslår, at undervisningen i stedet skal sigte på, at eleverne effektivt kan multiplicere etcifrede tal ved at kombinere resultatet af simple multiplikationer, de kan huske med mønstergenkendelse og tænkestrategier. Samtidig er det et mål, at eleverne - på samme måde som ved addition og subtraktion - udvikler deres talforståelse og forståelse af regningsarternes egenskaber.
Tællestrategier til multiplikation
Lige som addition og subtraktion bygger også multiplikation med etcifrede tal på tælling. Ved multiplikative situationer af typen ’lige store grupper’ skal det samlede antal elementer i et antal lige store grupper tælles. Udgangspunktet for undervisningen kan derfor være hverdagsproblemer, hvor eleverne skal tælle det samlede antal elementer i et antal lige store grupper:
I begyndelsen, hvor fokus er på forståelsen af multiplikation, kan eleverne fx arbejde med denne type situationer ved at bruge ’skip-tælling’ (fx 3, 6, 9, 12 etc.). (Kilde 2). Senere skal der arbejdes med tænkestrategier til multiplikation.
Forståelse af multiplikation
Udgangspunktet for at udvikle tænkestrategier til multiplikation er elevernes forståelse af multiplikation, herunder forståelse af:
- ’Enhed’
- Multiplikativ tænkning
- Forskellige repræsentationer
(Kilde 4)
1. Enhed
Når elever tæller det samlede antal i en mængde, der er opdelt i lige store grupper, er det vigtigt, at de er opmærksomme på størrelsen af de grupper, mængden er opdelt i – det vil sige enheden. Gruppen er blevet den nye enhed. Fx kan de række begge hænder op og enten tælle hænder (2) eller fingre (10): 2 gange enheden 5 er 10 . Tilsvarende når de har spillet vendespil og skal afgøre, hvem der har vundet, kan de enten tælle antal par eller antal kort, fx 7 stik gange enheden 2 er 14. Forståelse af den enhed man tæller, er vigtig for at forstå multiplikation. En del af forståelsen af enheden er, at eleverne skal lære at inddele i enheder, som så kan bruges til at tælle med, fx at se nedenstående som 4 grupper à 5 kvadrater. Der er 5, 10, 15, 20 kvadrater.

2. Multiplikativ tænkning
At tænke multiplikativt er at kunne håndtere tre elementer, der findes i enhver multiplikativ situation: En multiplikator, en multiplikand og et produkt.
- Multiplikatoren er det antal grupper, der skal tælles.
- Multiplikanden er det antal, der er i hver gruppe (eller den størrelse hver gruppe har).
- Produktet er det samlede antal.
På tegningen oven for er der $4$ grupper á $5$. Multiplikatoren er altså $4$, multiplikanden er $5$, og produktet er $20$. Normen er, at multiplikatoren skrives først, så det samlede antal kan repræsenteres med multiplikationen $4\cdot5=20$.
Når elever kan bruge disse tre elementer til at løse matematiske problemer, kan de tænke multiplikativt. I den konkrete situation oven for kan de fx tænke $4\cdot5$ som gentagen addition, dvs. $5+5+5+5$.
Eleverne kan fx arbejde med at udvikle multiplikativ tænkning gennem måling med forskellige enheder sådan, at der kommer fokus på enhed, antal enheder og antal i alt.
3. Forskellige repræsentationer
To repræsentationsformer er specielt vigtige, når eleverne skal tilegne sig effektive strategier til multiplikation, den dobbelte tallinje og rektangelmodellen. (Kilde 3)
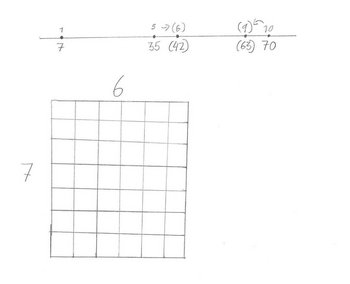
Den dobbelte tallinje er særligt velegnet til situationer, der kan beskrives med lige store grupper og multiplikative sammenligninger. På den dobbelte tallinje viser tallene over tallinjen antallet af enheder, og tallene under tallinjen viser det samlede antal. Arbejde med denne repræsentation er desuden meget velegnet til, at eleverne senere kan opnå forståelse af sammenhængen mellem multiplikation og division.
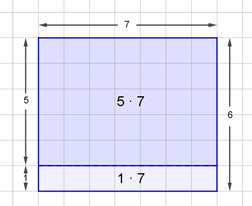
Rektangelmodellen er særligt velegnet til situationer, der kan beskrives med rektangulære mønstre. Både den kommutative lov, $a\cdot b=b\cdot a$, og den distributive lov, $a\cdot(b+c)=ab+ac$ kan illustreres med rektangelmodellen. I forhold til den distributive lov opdeles modellen i mindre dele, fx, kan $6\cdot7$ opdeles i $5\cdot7+1\cdot7$ (se figur herunder). Dette er en afgørende forståelse, når eleverne skal lære at multiplicere flercifrede tal.
Undervisning i tænkestrategier til multiplikation
Målet med undervisningen i etcifret multiplikation er, at eleverne bliver effektive ’regnere’, det vil sige at de kan huske en del resultater udenad, og at de kan bruge forskellige tænkestrategier fleksibelt til at regne hurtigt og sikkert. Der er i alt 100 multiplikationsstykker med to etcifrede tal, hvor den kommutative lov halverer antallet.
Eleverne kan udvikle tænkestrategier for multiplikation ud fra velkendte regler, systemer, mønstre og ræsonnementer:
- Regler for at multiplicere med 0 og 1 kan eleverne udlede af det indledende arbejde med multiplikation.
- At multiplicere med 2 svarer til at fordoble, som også er en væsentlig tænkestrategi ved addition.
- At multiplicere med 5 svarer til at gange med 10 og dele med 2, eller eleverne kan bruge mønsteret i tabellen.
- At multiplicere med 9 svarer til at gange med 10 og trække ’en gang’ (en enhed) fra, fx $9\cdot6$ giver $10\cdot6−1\cdot6=60−6=54$, eller eleverne kan bruge mønsteret i 9-tabellen.
…
(Kilde 1)
Tilbage er så 15 multiplikationsstykker, som eleverne skal lære at udføre med brug af andre tænkestrategier. Til dette er især skiptælling og den distributive lov nyttige. Herunder ses et eksempel på 7-tabellen, som oftest opleves som vanskelig for eleverne, blandt andet fordi den ikke har en tydelig sammenhæng med andre tabeller. 7-tabellen kan for eksempel undersøges ud fra en problemstilling om antal dage i et givet antal uger.
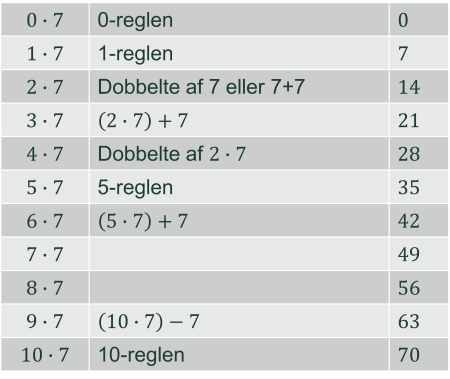
For at beregne $7\cdot7$ og $8\cdot7$ skal eleven bruge mere komplekse tænkestrategier:
Det kan fx være kendskab til kvadrattallene ($7\cdot7=49$ og dermed $8\cdot7=7\cdot7+7=49+7=56$)
Eller eleven kan bruge den distributive lov på mere avancerede måder, fx
$7\cdot7=5\cdot7+2\cdot7=35+14=49$
eller
$8\cdot7=10\cdot7−1\cdot7−1\cdot7=70−7−7=56$.
Ud over $8\cdot8$ kan de øvrige kombinationer i ’den lille tabel’ beregnes med de strategier, der er nævnt i tabellen.
Det er igen her værd at være opmærksom på, at tænkestrategier der udnytter generelle algebraiske regler er effektive til beregning samtidig med, at de styrker elevernes grundlag for senere udvikling af algebraisk tænkning.
TIL OVERVEJELSE I FAGTEAMET
- Hvilke problemstillinger oplever I, i arbejdet med multiplikation af etcifrede tal?
- Hvor stor en rolle spiller udenadslære, og hvor stor en rolle spiller udviklingen af tænkestrategier i jeres undervisning?
- Hvor ser I de største udfordringer i forhold til at eleverne skal lære etcifret multiplikation?
til: GRUNDSKOLE - Indskoling
emne: ALGEBRAUDGIVET: 2022
Forfatter
Kaj Østergaard
Lektor, ph.d.
VIA, Læreruddannelsen i Aarhus
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
- Kilpatrick, J., Swafford, J. & Findell, B. (Eds.) (2001). Adding it up. Helping children learning mathematics. National Research Council. Washington, DC: National Academy Press.
-
Fuson, K.C. (2003). Developing mathematical power in whole number operations. In J. Kilpatrick, W.G. Martin, & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 68–94). Reston, VA: National Council of Teachers of Mathematic
-
Treffers, A. (1991). Didactical background of a mathematics program for primary education. In: Streefland, L. (Ed.): Realistic Mathematics education in primary school: on the occasion of the opening of the Freudenthal Institute . Freudenthal Institute.
-
Lannin, J. (2013). Putting Essential Understanding of Multiplication and Division into Practice in Grades 3–5. Columbia, MI: National Council of Teachers of Mathematics.