Matematiske aktiviteter
Matematisk aktivitet består af tre trin: handling, formulering og validering. Læs beskrivelsen af de tre delaktiviteter, og se eksempler på, hvordan aktiviteten folder sig ud i typeopgaven, problemopgaven og projektopgaven.
Når man arbejder med en matematisk opgave – fx som elev i en undervisningssituation eller som forsker – kan man skelne mellem tre ret forskellige dele af den aktivitet, som løsningen kræver. (Kilde 1 og 2)
De tre dele af aktiviteten belyses i dette eksempel:
Eksempel: Hvor stort areal kan et rektangel have, når omkredsen skal være 5?
- Handling. Man bruger eller opsøger viden, som forekommer relevant for at løse opgaven, og prøver sig frem, fx med konkrete tal – man tegner, regner, bruger et digitalt værktøj, osv.
I eksemplet kan man prøve sig frem med forskellige sidelængder, sætte resultaterne op i en tabel, tegne de tilsvarende rektangler, osv.
- Formulering. Man formulerer så præcist som muligt en løsning af opgaven (evt. blot en hypotese) – løsningen kan være et tal, et argument, en model osv., afhængigt af hvad opgaven efterspørger.
I eksemplet kan man ud fra forudgående handling angive det største fundne areal (uden eksplicit overvejelse af alternative metoder, korrekthed osv.)
- Validering. Man efterprøver 'værdien' af en løsning, i matematik fx: korrekthed af resultat, om man har overset krav i opgaven, om andre løsninger eller argumenter er mere effektive, osv.
I eksemplet afvises den første hypotese som falsk, fordi afprøvning af andre sidelængder (yderligere handling) giver et større areal.
Løsningsarbejdet kan, som den korte beskrivelse ovenfor (og eksemplerne nedenfor) viser, veksle mellem de forskellige trin (herunder gentage dem flere gange). Det har konsekvenser for, hvad man kan lære af at løse opgaven – se de flg. eksempler.
Typeopgaver
Ved typeopgaver kan eleven straks anvende en kendt teknik (handling), som leder direkte til at formulere løsningen.
Eksempel: Find arealet af en cirkel med radius 5.
I eksemplet oversættes $r$ i den kendte arealformel til værdien 5, og denne værdi sættes ind: $A = π ⋅ 5^2 = 25π$, hvorefter man evt. udregner en tilnærmet værdi af det sidste tal på lommeregner. Der kræves i øvrigt også viden udover arealformlen: fx vide, at $x^2 = x ⋅x$ for et givet tal $x$. Formuleringen af resultatet følger mere eller mindre trivielt:
"Arealet er $25π$"
eller
"Arealet er ca. $78.5$".
Validering kan bestå i at 'kontrollere', at handlingen (den kendte teknik) blev udført rigtigt. Man kan også lave andre former for kontrol, i eksemplet fx en tegning på kvadreret papir, hvor optælling af kvadrater viser, at resultatet "ca. $78.5$" er rimeligt.
Men det er desværre almindeligt i undervisningssammenhæng (fra grundskole til universitet), at eleven ikke selv validerer egne løsninger, men overlader dette til læreren. At løse en typeopgave kan stadig give udbytte, især mere rutine i brug af en kendt teknik. Mange forskellige opgaver af samme type kan også give erfaring med teknikkens brug i forskellige mere eller mindre krævende tilfælde. Men hvis eleverne undlader validering (evt. også en klar formulering af resultatet), bliver udbyttet mindre, idet de ikke tilegner sig metoder til at kontrollere eget arbejde, så de fx opdager evt. fejl. Og så kan udbyttet af arbejdet med typeopgaver indskrænke sig til mekanisk at kunne udføre en teknik – uden indsigt i, hvad opgaven og dens resultat betyder, hvorfor teknikken er gyldig, og om der er regnet rigtigt. Da matematik på alle klassetrin omfatter mange forskellige teknikker, kan det også føre til, at eleven blander teknikker sammen, bruger en teknik, som egentlig ikke er relevant for opgaven, osv.
Alle matematiklærere oplever sådanne resultater af fejlslagent arbejde med typeopgaver, og den matematikdidaktiske litteratur er også righoldig på undersøgelser, der bekræfter, at mange elever udvikler en 'instrumentel' tilgang til matematikopgaver (se fx Kilde 3 og 4).
Problemopgaver
Når opgaven er en problemopgave, kan eleverne handle ved at bruge nogle af de teknikker, de kender.
Eksempel: Hvor stort areal kan et rektangel have, når omkredsen skal være 5?
I eksemplet kan man fx konstruere nogle rektangler med omkreds 5 og beregne deres areal, og man kan opstille sine beregninger i en tabel:
| Bredde | 2 | 1.5 | 1 | 0.5 | 0.25 |
|---|---|---|---|---|---|
| Højde | 0.5 | 1 | 1.5 | 2 | 2.25 |
| Areal | 1 | 1.5 | 1.5 | 1 | 0.5625 |
Ud fra den kendte teknik til at beregne omkreds af et rektangel, som to gange bredde plus to gange højde, indses det (fx ved at se på eksempler som i tabel 1), at når omkredsen skal være 5, må både bredde og højde være mindre end $2.5$. Desuden ses det, at når bredden er valgt, kan man finde højden som $2.5$ minus bredden. Arealet findes nu ved at gange bredde med højde. Så får man forskellige arealer som vist i tabel 1, hvor det største areal er $1.5$. Det kunne være en formulering af et svar:
"Det størst mulige areal er $1.5$."
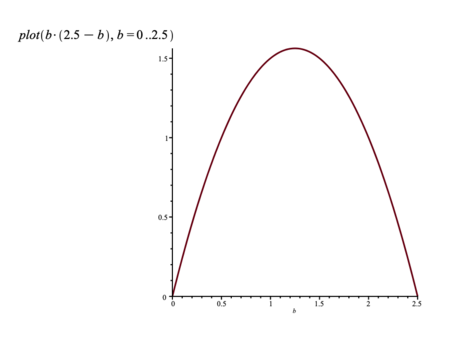
Men prøver man med andre værdier (mere handling), fx en bredde på $1.4$, får man højden $1.1$, og arealet bliver nu: $1.4⋅1.1 = 1.54$. Det første svar er dermed valideret negativt (det var forkert), idet $1.54$ faktisk er større end $1.5$. Samtidig indser man måske, at det ikke er nok at prøve sig frem. Man må finde en mere generel metode. At opgaven er en problemopgave, betyder, at eleven ikke kender en sådan metode, men alligevel har viden, som gør det muligt at finde en sådan. Det kunne i Danmark være tilfældet i grundskolens ældste klasser, eller i hvert fald i 1.g. For eksempel kunne eleven, afhængigt forudsætninger, opstille en algebraisk model for problemet ved at indføre en variabel $b$ som angiver rektanglets bredde. Nogle elever vil have behov for stilladsering. Den indsigt, at højden er $2.5$ minus bredden ($b$), kan nu udnyttes til at opskrive rektanglets areal som $b⋅2.5−b^2$. Dette variabeludtryk bestemmer en andengradsfunktion. Grafen kan hurtigt tegnes med et digitalt værktøj (se figur 1).
Grafen er en parabel. Den synes at være 'symmetrisk' omkring en lodret linje gennem det tal, som ligger midt mellem $0$ og $2.5$ – altså $b=1.25$. Her ses værdien af arealet at være størst (lidt større end $1.5$). Den præcise værdi af det størst mulige areal er derfor
$1.25 ⋅ 1.25 = 1.5625$
Vi ser også, at rektanglet med størst areal faktisk er et kvadrat. Det ville nogen elever måske have gættet på fra starten. Men valideringen af et sådant gæt ville stadig mangle.
Løsningen kan i øvrigt yderligere bekræftes ved at prøve med andre bredder, fx tæt på $1.25$, hvor arealet ganske rigtigt viser sig at være lidt mindre. I gymnasiet vil man også kunne præcisere valideringen på andre måder, fx ved at bruge toppunktsformlen for en parabel, CAS (hvis man har et matematikværktøj med optimeringsfunktion, evt. kombineret med regression på værdier som i tabel 1), differentialregning i en eller flere variable eller fuldstændiggørelse af kvadratet på det nævnte andengradspolynomium. Eleverne kunne måske endda generalisere metoderne til at bestemme det maksimale areal af et rektangel med en vilkårlig givet omkreds $C$, nemlig $C^2/16$. (Man erstatter $2.5$ med $C/2$ i udtrykket for parablen; andenkoordinaten for toppunktet bliver så $C^2/16$).
Om opgaven ligefrem er en 'typeopgave' afhænger så af, om eleverne har erfaring med at opstille algebraiske modeller og af deres algebraiske viden. En langt simplere løsning end de ovennævnte fås således, hvis man kender uligheden
$ab\leq\left(\frac{a+b}{2}\right)^2$
og så bruger den på højde $a$ og bredde $b$ af et vilkårligt rektangel. Så ser vi, at arealet er højst
$\left(\frac{a+b}{2}\right)^2$
og også at denne maksimale værdi faktisk realiseres for et kvadrat (med $a=b$ bliver uligheden ovenfor til en identitet, så arealet er med dette valg maksimalt). Hvis omkredsen er $C = 2(a+b)$, er det maksimale areal altså $C^2/16$ (Note 1)
Opgaven kan altså løses på mange forskellige måder, afhængigt af elevernes forudsætninger. I eksemplet vil eleverne næppe kunne bruge en standardteknik. Når de alligevel kan komme frem til løsninger, men bruger forskellige metoder, så opstår et naturligt behov hos eleverne for at sammenligne fremgangsmåder og resultater – og validere dem. Den matematiske aktivitet bliver mere righoldig – både i formulerings- og valideringssituationen.
Projektopgaver
Projektopgaver muliggør, ligesom problemopgaver gør det, righoldigt arbejde med alle dele af matematisk aktivitet.
Eksempel: Hvordan bestemmes arealet af en trekant ud fra sidelængderne?
Vi vil ikke gå i detaljer med eksemplet, men blot notere, at man også kan arbejde med denne opgave på både grundskole- og gymnasieniveau. (Kilde 5)
En særskilt udfordring består her i at opsøge og behandle information fra eksterne kilder, særligt formulering og validering af Herons formel. Men også handling og formulering, som fokuserer på specialtilfælde, hvor elevernes forudsætninger rækker – i eksemplet, fx retvinklede og ligesidede trekanter – kan være vigtige elementer i arbejdet med sådanne opgaver. Arbejdet med en projektopgave vil typisk strække sig over mere end én lektion og måske også omfatte en del hjemmearbejde for eleverne og tilhørende vejledning for læreren.
Validering er vigtigt og vanskeligt
Mens handling og formulering altid indgår i et eller andet omfang i elevernes matematiske aktivitet med en opgave, er validering både vanskeligt og vigtigt at engagere eleverne i. Validering er vanskeligt, fordi elevernes erfaring fra matematikundervisning generelt kan være, at "validering er lærerens ansvar." Oplevelsen af, at "læreren retter opgaverne" kan med tiden udvikle en bekvem og problematisk hjælpeløshed hos eleverne: De fralægger sig ethvert ansvar for at kontrollere gyldigheden af egne løsninger. (Kilde 4)
Validering er vigtigt, fordi svar, der alene er formuleret på basis af handling, mangler noget essentielt, nemlig overvejelse af værdien af svaret og metoden til at nå frem til det. I mange matematiske opgaver er løsninger enten korrekte eller ej; det er en fundamental erfaring, at man kan skaffe sig vished herom, og at en konklusion i mange tilfælde følger med logisk nødvendighed. I andre tilfælde – fx opgaver, der drejer sig om at opstille en model på basis af et datamateriale – er overvejelse af løsningens kvalitet, og argumenter herfor, en væsentlig del af opgaveløsningen, selv om man ikke kan tale om logisk nødvendighed af svaret. Og i alle typer af opgaver kan forskellige løsningsmetoder have forskellige kvaliteter, såsom klarhed og generalitet.
Uden validering er den matematiske aktivitet ikke komplet. I det første eksempel ovenfor med arealer af rektangler kan 'svaret' (et kvadrat) måske hurtigt opstå som et gæt eller en intuition, men selv da er validering en forudsætning for, at der udvikles matematisk viden (som aldrig bare er gætværk eller synspunkter).
til: GRUNDSKOLE, ERHVERVSSKOLE, GYMNASIE
emne: UNDERVISNINGSPLANLÆGNING
UDGIVET: 2022
Forfatter
Carl Winsløw
Professor
Institut for Naturfagenes Didaktik, KU
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder og noter
KILDER
- Brousseau, G. (1997). Didactical Situations in Mathematics. Dordrecht: Kluwer.
- Winsløw, C. (2006). Didaktiske Elementer: en introduktion til matematikkens og naturfagenes didaktik. Kap 7. København: Biofolia.
- Skemp, R. (1976). Relational Understanding and Instrumental Understanding, Mathematics Teaching, 77, 20-26.
- Sierpinska, A. (2007). I need the teacher to tell me if I am right or wrong. In Woo, J. H., Lew, H. C., Park, K. S. & Seo, D. Y. (Red.). Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, 1, 45-64. Seoul: PME.
- Rubin, J. (2013). Heron's Formula. Lokaliseret 01.11.21 på: https://www.juliantrubin.com/encyclopedia/mathematics/heron_formula.html
NOTER
1. Uligheden, som gælder for reelle tal $a$ og $b$, følger af at $(𝑎+𝑏)^2−(𝑎−𝑏)^2=4𝑎𝑏$. Se mere om denne og beslægtede uligheder på en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means