Matematiske ræsonnementer i indskolingen

I eksemplet skal eleverne argumentere for hypotesen 'Ulige + ulige = lige'. Aktiviteten er afprøvet i en 3.-klasse.

Aktiviteten illustrerer, hvordan elever arbejder i ræsonnementscyklussen (se figur 1), og hvordan elevers ræsonnementer hænger sammen med de fælles forståelser, der allerede er i klassen. (Kilde 1)

Ræsonnementerne er opbygget forskelligt, men fælles for dem er, at de:

bygger på et fundament, fx et empirisk eller et mere autoritativt fundament
anvender en bestemt måde at overbevise på, fx laver modbeviser eller systematiske opskrivninger
er udtrykt via en repræsentation, fx mundtlige eller mere symbolske repræsentationer.

Læs om ræsonnementscyklussen og om opbygningen af ræsonnementer

Aktivitet med hypotesen: 'Ulige + ulige = lige'

I aktiviteten skal eleverne undersøge, opstille og argumentere for hypotesen om, at man får et lige eller et ulige tal, når man lægger to ulige tal sammen.

De afprøver forskellige eksempler, $3 + 5$, $5 + 7$ og $7 + 9$, og i samarbejde med deres lærer formulerer de følgende hypotese, som læreren skriver på tavlen:

'Ulige + ulige = lige'

Læreren udfordrer derefter eleverne til at argumentere for denne hypotese.

Eleverne arbejder i grupper med dette, og de kommer med flere forskellige argumenter.

En elev giver udtryk for, at det er umuligt at redegøre for summen af alle par af ulige tal, fordi rækken af de ulige tal vil forsætte for evigt:

"Vi kan ikke bevise, at det virker for alle tal."

En anden elev er ikke enig. Hun mener, at når hun har vist det for 18 forskellige par af ulige tal, så må deres hypotese gælde altid.

Elevens argument er funderet på empiriske undersøgelser, og læreren vil nu gerne udfordre elevernes forestillinger om dels, at man ikke kan bevise hypotesen for ALLE ulige tal, og dels, at det ikke er nok at vise, at hypotesen gælder for enkelte ulige tal. Læreren minder derfor eleverne om, hvordan de i en tidligere lektion har defineret ulige og lige tal.

Læreren skriver følgende på tavlen:

- Ulige tal: Hvis du deler ulige tal med 2, så vil der altid være én i overskud.
- Lige tal: Hvis du deler lige tal med 2, vil der ikke være noget i overskud.

Eleverne bliver nu opfordret til at bruge disse definitioner i deres argumentation.

Ved opsamlingen giver en elev ved navn Betsy udtryk for, at hun har et bevis for påstanden.

I hendes argumentation bliver den visuelle repræsentation afgørende for forståelsen:

Betsy:

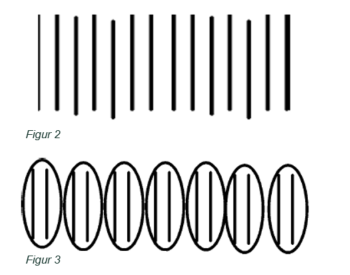
"… hvis vi har 7 linjer plus 7 linjer [hun tegner 14 linjer på tavlen] (se figur 2), og hvis vi skal fordele dem i cirkler med to [hun tegner cirkler omkring linjerne i par og vender sig om mod klassen] (se figur 3)… hvis du tilføjer et ulige tal til et andet ulige tal, så vil det svare til et lige antal, fordi at alle ulige tal, det er de tal, som hvis du tegner cirkler om dem to og to, er der 1 tilbage, så hvis du... plusser 1, uhm, eller hvis du plusser et andet ulige tal, så de 2, der er tilbage, grupperer sig sammen, og det bliver et nyt lige tal…"

Efterfølgende diskuterer eleverne, om Betsys argument holder.

En elev er uenig med Betsy, fordi man ikke kan være sikker på, at det gælder for alle tal, fx store ukendte tal.
En anden elev mener, at argumentet holder:

"… hun sagde ikke, at det skulle være to bestemte tal, det kan være alle mulige ulige tal, fordi alle ulige tal har 1 i overskud". (Kilde 1)

Betsys argument

I modsætning til de argumenter, eleverne tidligere har bidraget med, har Betsys argument et fundament, der tager udgangspunkt i klassens fælles accepterede definitioner af ulige og lige tal.

Disse definitioner var grundlaget for hendes kæde af argumenter, der blev bundet sammen med ord som 'hvis… så', 'fordi' og afsluttet med en formulering af sætningen 'ulige+ulige=lige'. Argumentationen bliver sammenhængende, fordi hvert led i kæden hænger logisk sammen. Man kan se denne sammenhæng i sproget: Hvis definitionerne for ulige og lige tal er sande, så må det gælde at…

Opbygningen af Betsys argument var således en logisk deduktion fra de tidligere definitioner, og det involverede en analyse af det, der følger af definitionen af lige og ulige tal. Betsys argument var en mundtlig repræsentation suppleret med en visualisering, hvor hun brugte sit hverdagssprog til at udtrykke sin argumentation. Hun visualiserer naturlige tal med et antal streger, som hun grupperer i 2 for at illustrere et lige tal (ingen overskydende streger) og et ulige tal (1 overskydende streg).

Betsys argument er ikke et eksempel på et formelt matematisk bevis, som matematikere ville give til udsagnet 'ulige + ulige = lige'; men Betsys argument er i overensstemmelse med klassens fundament, argumentationsmåder og repræsentationsformer, og hendes ræsonnement kan derfor ses som et skridt i retning mod det formelle og som et udtryk for en passende balance mellem de matematiske kompetencer, elever typisk har i tredje klasse, og matematikfaget som disciplin.

Selv om Betsys ræsonnement ikke kan anses som et formelt set korrekt deduktivt bevis, vil det godt kunne anses som 'et slags bevis' i indskolingen.

Det er rimeligt at antage, at elever, der ligesom Betsy arbejder med denne type af ræsonnementer allerede i tredje klasse, er godt forberedt på at følge og selv udvikle matematiske beviser senere i skoleforløbet og på ungdomsuddannelserne.