Hvordan undgås negative black box-effekter?

Digitale matematikværktøjers tilstedeværelse i klasserummet kan adresseres eksplicit i forberedelsen af undervisningen med afdækning af potentialerne for elevernes læring. Her tages der eksplicit stilling til, hvilke elementer af aktiviteterne der kan understøtte elevernes læring. I forskningen har man ladet sig inspirere af terminologien fra forretningsverdenen om in- og outsourcing. Se eksempler på aktiviteter, hvor black box-effekten undgås.

In- og outsourcing

For at give et mere nuanceret billede af, hvornår og til hvad det er relevant at trække på digitale matematikværktøjer herunder CAS-redskaber, har Bang, Grønbæk og Larsen ladet sig inspirere af terminologien fra forretningsverdenen vedrørende in- og outsourcing med reference til optimering af virksomhedens produktivitet. (Kilde 1)

I matematikundervisningen er matematiklæring produktet, og læreren, der skal orkestrere de ressourcer, eleverne skal bruge for at producere matematiklæring, er lederen af produktionen. Og elevernes eksisterende viden, færdigheder og kompetencer (matematiske og computerrelaterede) er ressourcerne. Det omfatter elevernes anvendelse af dynamiske repræsentationer, CAS-redskaber og i det hele taget brug af resultater, de kan genere med deres digitale matematikværktøjer.

Som lærer planlægger og udvikler man undervisningsaktiviteter på grundlag af matematisk og matematikdidaktisk viden om det faglige indhold, erfaringer med matematikundervisning generelt og eventuelle erfaringer fra undervisning i det aktuelle indhold samt erfaringer med den konkrete klasse. Herudfra danner man sig forventninger om, hvilke typiske misforståelser ved tidligere begreber der kan fremkaldes og volde eleverne vanskeligheder i det pågældende emne, samt om hvilke principielle udfordringer eleverne skal overvinde ved læring af de centrale begreber i emnet. Sammen med viden om, hvordan emnet rammesættes i læreplanen, lærebøger og indgår i eksamensopgaver, danner sådanne forventninger grundlaget for tilrettelæggelse af undervisningsaktiviteter og – forløb.

Hvis undervisningen skal understøtte elevernes udvikling af stærke schemes, må den planlægges, så der kan tages højde for og reageres på elevernes demonstration af såvel løsningsorienteret (pragmatisk) som erkendelsesorienteret (epistemologisk) tilgang til brugen af et matematikværktøj. Både den løsningsorienterede og erkendelsesorienterede tilgang kan være relevant og ønskværdig. Det er læringsmålet for den nye aktivitet og dennes rammesætning, der afgør relevansen. Indhøstes læringsmålet ikke i tilstrækkelig grad, må aktivitet eller rammer justeres, herunder brugen af digitale matematikværktøjer.

Læs mere om skema og schemes i
Fra værktøj til personligt instrument og CAS, begrebsdannelse og negativ black box-effekt.

For at skabe dette rette læringspotentiale skal det afgøres, hvilke elementer i aktiviteterne der skal insources, og hvilke der med fordel kan outsources til et matematikprogram.
Bang, Grønbæk og Larsen definerer out-sourcing i matematikundervisningen som:

"Out-sourcing af en matematisk aktivitet betyder at allokere den til en ressource til gengæld for at afgive kontrol over processen." (Kilde 1)

Center for Computerbaseret Matematikundervisning (CMU) har erfaringer med at vejlede lærere i brugen af computere i matematikundervisningen. På baggrund af lærernes egne analyser af deres klasser og undervisningsaktiviteter, formulerer de en undervisningsproblematik som de vil adressere.

I CMU-projekterne har argumenterne for outsourcing og anvendelse af digitale matematikværktøjer ofte en pragmatisk værdi, selv om de også skal understøtte epistemiske læringsmål.

Læs også om Løsnings- og erkendelsesorienteret brug af CAS.

Skyderfælden – en uheldig black box

Bang, Grønbæk og Larsen har set på brugen af computeren ved introduktionen af differentialregning og tretrinsreglen, hvor målet er at forstå tangenthældning og grænseværdibegrebet. Inspireret af lærebogsmaterialet outsources grænseovergangen for differenskvotient til differentialkvotient i denne sammenhæng til et matematikværktøj gennem brug af skydere. Det viser sig at være problematisk på flere måder. (Kilde 1)

Brugen af skydere kan i sig selv repræsentere en uheldig black box, hvilket hos Bang, Grønbæk og Larsen kaldes 'skyderfælden'. (Kilde 2)

Skyderfælden er et eksempel på black boxing, der illustrerer kernen i de udfordringer, identificeret i efteruddannelsestilbuddet om computerbaseret matematikundervisning hos CMU. Sammenfattende udpeges de tre største udfordringer ved computerbaseret matematikundervisning til at være:

et design-dilemma mellem forestillede læringsstrategier og elevernes faktiske aktiviteter;
vigtigheden af lærernes strategiske valg angående 'out-sourcing' af opgaver til matematikprogrammer
betydningen af 'instrumentel genese'. (Kilde 2)

De to sidste vedrører særligt lærerens bevidsthed omkring valg og fravalg, når undervisningen tilrettelæggelse. Begrebet instrumentel genese og at aktiviteten giver eleverne mulighed for at udvikle dette, bør være centralt i tilrettelæggelsen af aktiviteter med matematikværktøjer.

'Skyderfælden' er et eksempel på design-dilemmaet, der kan opstå i situationen, hvor den velmenende lærer har lavet et dokument i et matematikværktøj, der fx skal understøtte elevernes undersøgelse af koefficienternes og konstantens betydning for andengradspolynomiets graf. Tanken er at eleverne ved at trække i skyderne, måske en ad gangen, ændrer på grafens udseende og dermed indser betydningen af de to koefficienter og konstanten.

Problemet er bare, at ikke alle elever kobler deres ændring af talværdierne på skyderen med noget, der ændrer funktionsforskriften og dermed grafen. Denne form for aktivitet forudsætter en form for instrumentering. Undersøgelsen er ikke rigtigt undersøgende og mangler en mulighed for, at eleverne kan vurdere konsekvenserne af deres handlinger, så det bliver klart, hvilken betydning deres brug af skyderen – og dermed valg af talværdi – mere præcist har for grafens form og placering.

Aktiviteter, hvor black box-effekt kan undgås

Skal eleverne erhverve sig viden om fx koefficienter og konstants betydning for udseendet af parablen med et matematikværktøj, kræver det en anden epistemisk tilgang. Fx aktiviteter, hvor eleverne ved hjælp af et matematikværktøj skal finde eller justere forskrifter, så parablerne opfylder forskellige kriterier.

Eksempler

1.

Et eksempel er at genskabe McDonald’s logo så præcist som muligt.

Illustration af genskabt McDonalds-logo i Geogebra

Figuren viser logoet for McDonald’s – det gule M. Figuren er fremstillet i GeoGebra.

Udfordringen til eleverne er at bestemme forskrifter for to parabler, der bedst muligt – efter elevernes egen vurdering – gengiver logoet. De to røde parabler viser en løsning, der kan forbedres.

2.

Lav et arbejdsark med en sinuskurve, der illuderer bølger i havet, og bed eleverne indtegne 4 små både i form af parabler på bølgerne, hvor en skal ligge i en bølgetop, en i en dal, en imellem top og dal samt én, der tydeligvis er kæntret (som vender på hovedet).

Illustration af opgaven i Geogebra

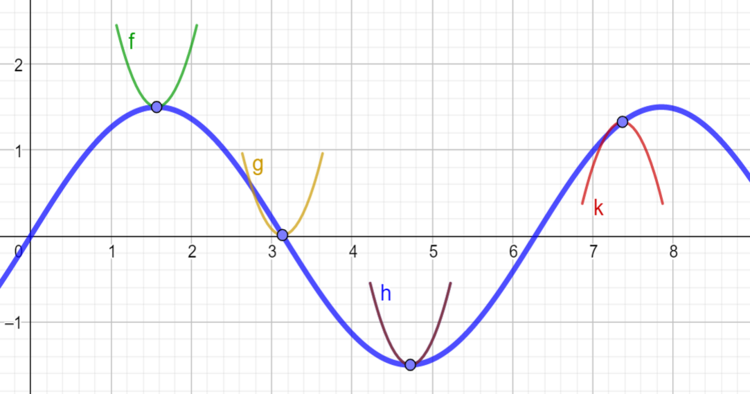
Figuren viser grafen for en funktion med forskriften $f(x) = A sin(x)$ som en model for bølger i havet. Figuren er fremstillet i GeoGebra.

Udfordringen til eleverne er at bestemme forskrifter for parablerne ud fra den blå graf og en sproglig beskrivelse af, hvor bådene skal placeres.

3.

Eleverne kan arbejde med at fremstille og opløse andengradspolynomier som en sum af en konstant funktion, $c$, en ligefrem proportionalitet, $bx$, og en 'grundparabel' med toppunkt i $(0,0)$, $ax^2$. Eleverne kan så udfordres til at udføre sammenlægningen af disse funktioner i såvel en numerisk (tabelmæssig), algebraisk som en grafisk repræsentation, og til at sammenfatte det hele i et digitalt matematikværktøj.

Illustration af fremstilling og opløsningen af andengradspolynomium i Geogebra

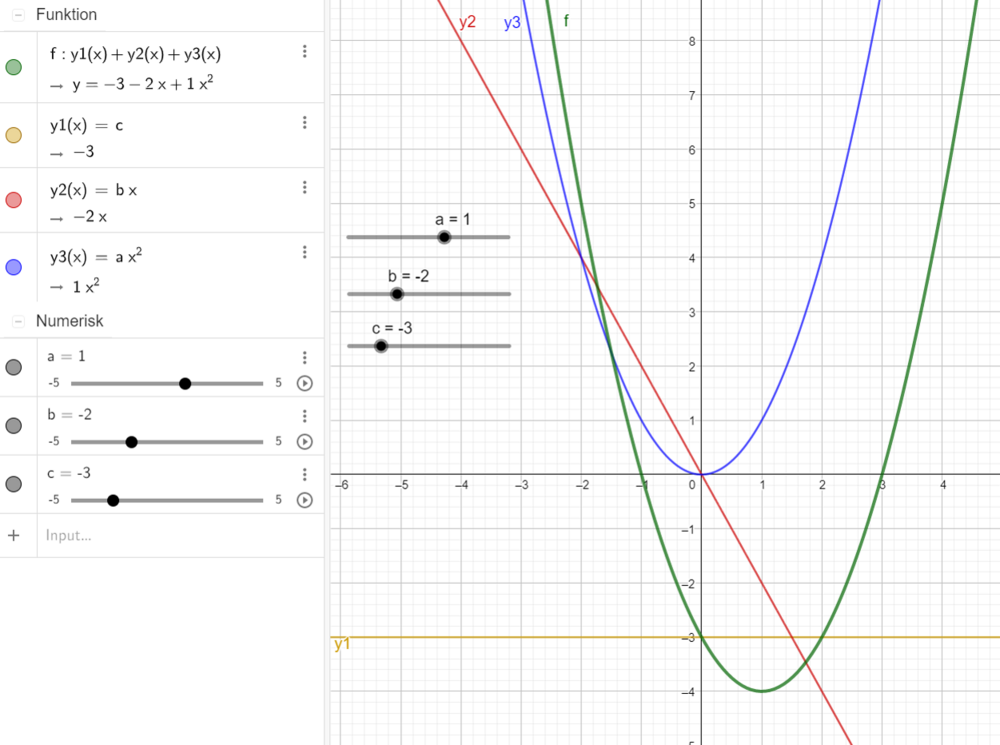
Figuren viser grafen for et andengradspolynomium (den grønne parabel) som summen af tre funktioner. Figuren er fremstillet i GeoGebra.

Den kan fremstilles som summen af en konstant funktion, $y = c$, en ligefrem proportionalitet, $y = bx$, og en parabel med ligningen $y = a x^2$. Figuren er fremstillet i GeoGebra således, at parametrene $a$, $b$ og $c$ kan ændres med skydere.

De tre aktiviteter bidrager på forskellig måde til elevernes forståelse af betydningen af parametrene i et anden-grads-polynomium. De to første aktiviteter kræver, at eleverne forholder sig til definitionsmængden for hver parabel samt justerer parablernes placering i grafvinduet ved at justere parametrene. Den tredje aktivitet bidrager til at skabe sammenhæng til elevernes forståelse af lineære funktioner og til at styrke deres forståelse af en funktion som et matematisk objekt, der kan indgå i andre processer, her i en sum af funktioner i dets forskellige repræsentationsformer. Et dynamisk geometri program som GeoGebra er en ressource ved udvikling af undersøgende aktiviteter og et kraftfuldt værktøj for eleverne ved arbejde med sådanne aktiviteter. GeoGebra.com giver adgang til programmet, der er frit tilgængeligt og indeholder mange eksempler, der kan tjene som resurse ved udvikling af undersøgende aktiviteter.

Udfordringerne i relation til brug af matematikværktøjernes apps, der inkluderer skydere, knapper, måleværktøjer m.m. kan opsummeres således:

Appsene afspejler matematik, der primært er baseret på ikke-digitale forståelser og standarder.
De anvendte instrumentaliserede teknikker har en lav epistemisk værdi. Den instrumentelle genese kræver begrænset viden og metoder, hvilket giver anledning til overfladelæring. De konceptuelle elementer af de instrumenterede handleskemaer er utilstrækkelige med hensyn til intenderet kognition.
Matematisk [stofdidaktisk] analyse (om nogen) bag appsene er lavet uafhængigt af de anvendte teknikker.
Der mangler strategisk planlægning af outsourcing til CAS.
Undersøgelseselementerne er ikke ægte undersøgende. Resultaterne af tilladte manipulationer er prædefinerede. (Kilde 2)

Læs uddybende om Instrumentel genese og om Løsnings- og erkendelsesorienteret brug af CAS.

Udfordringer kan ses som designprincipper

Vender man udfordringerne om, kan de ses som designprincipper, hvor man eksplicit undersøger:

hvilken undervisningsmæssig udfordring man vil overkomme?
hvilken matematik indgår, hvad består den af, hvilke begreber og metoder indgår?
hvilke muligheder tilbyder matematikværktøjet? Er der centrale begreber eller processer, der omformes eller forsvinder i værktøjet, hvis vanlige aktiviteter outsources? Hvilke er centrale at beholde som 'papir og blyants'-aktiviteter?

Læs på CMU's hjemmeside en bredere analyse i en dansk kontekst om, hvordan ovenstående spørgsmål kan adresseres med eksempler på projekter gennemført ved danske gymnasier under supervision fra CMU.

Hovedpointen er, at de digitale matematikværktøjers tilstedeværelse i klasserummet skal adresseres eksplicit i forberedelsen af undervisningen med afdækning af potentialerne for elevernes læring. Der skal eksplicit tages stilling til, hvilke elementer af aktiviteterne der kan outsources, og hvilke der bør insources for på hver sin vis at understøtte elevernes læring.