Hvad siger forskningen?
Tekstens to første dele beskriver noget af det, vi ved fra forskning om
- relationen mellem elevers forståelse af de regnestrategier, de lærer, og elevernes færdigheder i beregninger. Hvordan hænger forståelse og færdigheder sammen i forbindelse med flercifrede beregninger?
- undervisning i regnestrategier. Hvilke tilgange ser ud til at kunne bidrage til, at eleverne lærer at regne med flercifrede tal på en hensigtsmæssig måde?
Den tredje del af teksten diskuterer, hvilken betydning den forskningsbaserede viden bør have for praksis i grundskolen.
Omdrejningspunktet i hele teksten er flercifrede beregninger med papir og blyant. Sådanne beregninger er tæt forbundet med især hovedregning og overslagsregning, men disse sider af sagen er ikke omtalt specifikt i teksten. Beregninger med regnetekniske hjælpemidler er en anden central del af grundskolens matematikundervisning, der heller ikke bliver omtalt her.
En regnestrategi er den måde, man håndterer de tal, der indgår i en beregning, med henblik på at finde frem til et resultat (kilde 1).
En algoritme til en beregning består af faste trin-for-trin-handlinger, der viser, hvordan man kan håndtere de tal, der indgår, for at finde frem til et resultat (kilde 3).
Relationen mellem forståelse og færdigheder
Traditionelt er elever i mange lande, herunder Danmark, blevet undervist i at følge en bestemt algoritme til beregninger med flercifrede tal. Forældrene til de nuværende elever i grundskolen har typisk fået vist trinnene i en algoritme, og derefter har de øvet sig på dem, så de blev i stand til at foretage korrekte beregninger (kilde 2). Elever, der har modtaget den form for undervisning, har imidlertid sjældent forstået, hvorfor algoritmen kan føre til disse korrekte beregninger. Det generelle billede er således, at vægten har været lagt på de færdighedsmæssige aspekter frem for de forståelsesmæssige aspekter. Det skyldes bl.a., at man længe har troet, at forståelse kom mere eller mindre automatisk gennem træning. Nogle lærere har dog undervist i de mere forståelsesmæssige sider af algoritmerne efter, at eleverne har lært algoritmen. Hos disse lærere har forståelse på den måde også spillet en rolle i undervisningen, men på en måde så færdigheder og forståelse har været adskilt.
Forskning har imidlertid dokumenteret, at der er en tæt sammenhæng mellem elevers forståelser af flercifrede beregninger og deres færdigheder i beregninger. Mere præcist er der forskningsmæssigt belæg for følgende to pointer:
- Elever, der er blevet undervist på den traditionelle måde, har vanskeligt ved at udvikle både forståelse for flercifrede tal og færdigheder i beregninger med disse tal (kilde 3).
De forståelsesmæssige problemer, der her omtales, kan fx handle om elever, der ikke kan udpege 1´ere, 10´ere og 100´ere i trecifrede tal eller om elever, der ikke kan demonstrere eller forklare ’tierveksling’ med konkrete materialer. De færdighedsmæssige problemer kan fx vedrøre elever, der glemmer et trin i algoritmen, eller bytter om på rækkefølgen af to trin.
- Elever, der har god forståelse for flercifrede tal, har typisk også gode færdigheder i beregninger med disse tal (kilde 3 og 4).
Der findes adskillige studier, der underbygger denne pointe (kilde 5). Blandt disse studier er et eksperiment, hvor forskere har fulgt en stor gruppe elever fra 1. klasse til 4. klasse (kilde 6). Undervejs blev både elevernes forståelse for flercifrede tal og deres færdigheder i flercifrede beregninger evalueret. Med henblik på at evaluere forståelse blev eleverne fx spurgt, om de kunne identificere antallet af 10´ere i et flercifret tal, repræsentere værdien af hvert ciffer med konkrete materialer og lave forskellige konkrete repræsentationer af flercifrede tal. Elevernes færdigheder blev evalueret gennem deres løsning af opgaver, som involverede addition og subtraktion med større og større tal op igennem klassetrinnene.
Studiet viste, at de elever, der demonstrerede den største forståelse for flercifrede tal, også opnåede de højeste scores i den færdighedsmæssige del af evalueringen. I tillæg viste studiet, at graden af den forståelse, elever udviser for flercifrede tal, kan bruges til at forudsige ikke alene deres nuværende færdigheder i beregninger med sådanne tal, men også deres fremtidige færdigheder. Nogle forskere har, på baggrund af flere studier, konkluderet, at der i et vist omfang er evidens for, at forståelse er grundlaget for at udvikle færdigheder, og at det ikke er hensigtsmæssigt at opøve færdigheder uafhængigt af forståelse (kilde 4).
Om undervisning i regnestrategier
De problemer, der er forbundet med den traditionelle algoritmeundervisning, har ført til udforskning af alternative tilgange til undervisning i flercifrede beregninger. De alternative tilgange har det tilfælles, at de i højere grad end den traditionelle tilgang søger at skabe sammenhæng mellem elevers forståelser af flercifrede tal og deres færdigheder i beregninger. De følgende tre pointer stammer fra studier om forskellige alternative tilgange til undervisning i flercifrede beregninger.
- Der findes flere forskellige undervisningsmæssige tilgange, som kan støtte elever til både at udvikle forståelse for og færdigheder i flercifrede beregninger (kilde 4).
Forskning har altså ikke udpeget en enkelt undervisningsmæssig tilgang til at være bedst, når målet er, at elever både skal udvikle forståelse og færdigheder knyttet til flercifrede beregninger - der er flere tilgange, som fungerer. De succesfulde tilgange har dog det tilfælles, at
- de lægger op til, at eleverne bruger strategier, de forstår.
- eleverne støttes til at fokusere på titalssystemets struktur og på, hvordan denne struktur kan bruges i beregninger.
- undervisningen foregår i en progression, der skal gøre de strategier, eleverne bruger, stadig mere effektive, men på en sådan måde, at de hele tiden er forståelige for eleverne.
- undervisningen foregår i en klasserumskultur, der lægger vægt på faglige dialoger og værdsætter forståelse, og hvor fejl bliver betragtet som en naturlig del af en læreproces.
- Hvis elever får mulighed for det og støtte til det, kan og vil de udtænke deres egne strategier til flercifrede beregninger (kilde 4).
Eksemplerne herunder viser to elevers strategier til hhv. addition og subtraktion (fra kilde 7, s. 20 og 22). Noterne i eksemplerne er typiske for elever, der udvikler deres egne strategier: De viser elevernes tænkning. Denne tænkning ser ud til at være forbundet med forståelse af bl.a. titalssystemets struktur (jf. punkt 1).
De fleste elever har brug for hjælp til at udtænke eller udvikle regnestrategier. Det gælder især i forbindelse med multiplikation og division. Forskning tyder på, at eleverne kan få en sådan hjælp ved at lytte til og skabe mening i andre elevers og lærerens forslag til fremgangsmåder. Især, hvis forklaringerne er understøttet af tegninger eller konkrete materialer.
- Konkrete materialer kan støtte en hensigtsmæssig faglig udvikling, men gør det kun under visse betingelser (kilde 4).
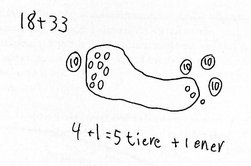

For mange elever kan det være en hjælp at bruge konkrete materialer som støtte til at udvikle eller forstå regnestrategier. Et sådant materiale kan fx bestå af klodser, der repræsenterer 1´ere, 10 ´ere, 100´ere osv. Det er imidlertid vigtigt, at eleverne får gode muligheder for at forbinde materialerne med de talstørrelser, de repræsenterer og de fremgangsmåder, der illustreres gennem brugen af dem. I modsat fald kan det være, at eleverne slet ikke ser sammenhængen mellem de handlinger, de foretager med materialerne, og det materialerne skal illustrere.
Hvilke konsekvenser skal den forskningsbaserede viden have?
På baggrund af de omtalte forskningsresultater er det naturligt, at læseplaner tager afstand fra den traditionelle opøvelse af algoritmer og i stedet lægger vægt på, at eleverne skal udvikle forståelse for de strategier, de bruger. Det skyldes ikke, at det nu (nødvendigvis) er mindre vigtigt, at eleverne også opnår færdigheder i beregninger. Det skyldes snarere, at udvikling af færdigheder hænger sammen med udvikling af forståelse.
Et mere åbent spørgsmål er, hvordan undervisningen i flercifrede beregninger kan se ud, når den i højere grad end tidligere skal fokusere på forståelse. En gruppe af forskere og undervisere har argumenteret for, at undervisningen bør tage udgangspunkt i elevernes egne faglige ideer og bør være rettet mod, at de udvikler regnestrategier, som de kan bruge fleksibelt (fx kilde 8).
At en person kan bruge regnestrategier fleksibelt vil sige, at personen råder over forskellige mulige strategier til beregninger og kan vælge en strategi, der er hensigtsmæssig for hende/ham i en bestemt beregning (kilde 1).
En metode til at regne med flercifrede tal opfattes i denne sammenhæng som en på forhånd fastlagt strategi og skrivemåde, der kan bruges generelt i forbindelse med en regningsart.
I talbaserede metoder håndterer man tallene i overensstemmelse med den værdi, de repræsenterer (tallet 75 kan fx opdeles i 70 og 5). Sådanne metoder står i modsætning til cifferbaserede metoder, hvor man håndterer cifrene i tallene uden at tænke på den værdi, de repræsenterer (tallet 75 kan fx opdeles i cifrene 7 og 5).
Ifølge disse forskere sikrer en sådan tilgang til undervisningen for det første, at talbehandlingen er direkte forbundet med den forståelse, eleverne har, og for det andet at undervisningen giver gode muligheder for, at eleverne kan udvikle kompetencer som problemløsning og ræsonnement, hvilket dybest set er formålet (se også Hvad er formålet?). Fortalerne for et øget fokus på bruge regnestrategier fleksibelt fremhæver desuden, at når først elever har lært en bestemt algoritme, så vil de være tilbøjelige til at bruge denne. Der opstår på den måde en risiko for, at eleverne mister blik for, at andre strategier end algoritmen kan være smarte at bruge i en given beregning. Fx kan det i forbindelse med beregningen af $987-888$ være mere hensigtsmæssigt at tænke, at ’afstanden fra 888 til 987 er 100 minus 1’, fremfor at bruge en algoritme (kilde 3).
En anden gruppe forskere er enige i, at undervisningen bør udgangspunkt i elevernes egne faglige ideer til beregninger, men disse ideer bør støttes sådan, at eleverne kommer til at kunne bruge en såkaldt talbaseret metode til hver regningsart (fx kilde 9). En ofte brugt metafor for denne undervisningsstrategi er, at eleverne skal deltage i udviklingen af beregningsmetoder (Se også Addition og subtraktion og Mulitplikation og division). Eleverne får på den måde gode muligheder for at udvikle metoder, som på den ene side er rimelig effektive, og på den anden side er forståelige for dem. Ifølge disse forskere vil en sådan undervisning kunne bidrage til et dobbelt formål: at eleverne får redskaber, de kan bruge i hverdagen, og at de udvikler alsidige kompetencer (se også Hvad er formålet?).
En tredje gruppe forskere argumenterer for, at metoder til beregninger og fleksibelt brug af regnestrategier ikke nødvendigvis er modsætninger. De foreslår, at undervisningen primært sigter på, at eleverne bliver i stand til at regne fleksibelt, men at der i det repertoire af strategier, som eleverne komme til at råde over, også kan indgå en metode til hver regningsart. Undervisningen skal med andre ord både støtte elevernes udvikling af forskellige regnestrategier og af en metode, som de kan gribe til, hvis de i en bestemt beregning ikke kan komme på en smartere strategi.
TIL OVERVEJELSE I FAGTEAMET
- Hvor placerer I jer i diskussionen om algoritmer, regnestrategier og elevers deltagelse i udvikling af metoder til flercifrede beregninger? I jeres diskussion kan I evt. inddrage de fire opgaver herunder. Hvad kan være gået galt for de elever, der har skrevet de mest typiske fejlsvar? Opgaverne er fra folkeskolens prøve uden hjælpemidler, maj 2019.
| Opgaver | Procentdel korrekte svar | Mest typiske fejlsvar |
|---|---|---|
5.1 1072 + 4038 5.2 701 - 149 5.3 350 · 9 5.4 7021: 7 | 93,6 % af eleverne 71,3 % af eleverne 83,4 % af eleverne 66,6 % af eleverne | 5100 (34,6 % af de forkerte svar) 462 (14,4 % af de forkerte svar) 3050 (6,7 % af de forkerte svar) 103 (51,3 % af de forkerte svar) |
til: GRUNDSKOLE - Indskoling og mellemtrin
emne: ALGEBRAUDGIVET: 2022
Forfatter
Thomas Kaas
Lektor, ph.d.
Professionshøjskolen Absalon
Udgiver
Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer
Kilder
-
Hickendorff, M., Torbeyns J. & Verschaffel L. (2019), Multi-digit Addition, Subtraction, Multiplication, and Division Strategies. I Fritz A., Haase V.G., Räsänen P. (Red.), International Handbook of Mathematical Learning Difficulties, s. 543-560. Switzerland: Springer. Doi: 10.1007/978-3-319-97148-3_32
-
Jørgensen, Anna (2000). Børnenes egne algoritmer. Hvorfor? Hvordan? I M. Jansen & H. N. Jensen (red.), Undervisning i matematik (s. 61-100). Vejle: Kroghs Forlag
-
Verschaffel, L., Greer, B. & DeCorte, E. (2007). Whole Number Concepts and Operations. I F. Lester (red.), Second handbook of research on mathematics teaching and learning (s. 557-628). Charlotte, NC: Information Age Publishing.
-
Kilpatrick, J., Swafford, J. & Findell, B. (red.) (2001). Adding it up. Helping children learning mathematics. National Research Council. Washington, DC: National Academy Press.
-
Rittle-Johnson, B. & Siegler, R. S. (1998). The relation between conceptual and procedural knowledge in learning mathematics: A review. I C. Donlan (red.), The development of mathematical skills (s. 75–110). East Sussex, UK: Psychology Press.
-
Hiebert, J. & Wearne, D. (1996). Instruction, understanding, and skill in multidigitaddition and subtraction. Cognition and Instruction, 14, 251–283.
-
Beck, H. J., Jørgensen, A., Kaas, T. & Petersen, L. Ø. (2009). Matematik for lærere. Arbejdskort 1A. Undersøge, konstruere og argumentere. København: Gyldendal.
-
Grove, M. (2023). Sæt fokus på regnestrategier, og lær eleverne at tænke fleksibelt. EMU. Danmarks læringsportal. Hentet fra (Sæt fokus på regnestrategier, og lær eleverne at tænke fleksibelt | emu danmarks læringsportal.
-
van Galen, F. H. J., & Gravemeijer, K. P. E. (2003). Facts and algorithms as products of students' own mathematical activity. A research companion to principles and standards for school mathematics, 114-122.