Du er her: Forside Tema At regne med etcifrede tal Undervisning i addition og subtraktion af etcifrede tal

Undervisning i addition og subtraktion af etcifrede tal

Elever udvikler ofte strategier til regning med etcifrede tal i en bestemt rækkefølge eller progression. Progressionen består af tre typer af strategier både, når det drejer sig om addition og subtraktion. Læs om de tre strategier og se, hvordan læreren kan støtte elevernes udvikling af disse strategier og støtte dem i at gå fra konkret til abstrakt tænkning i arbejdet med addition og subtraktion af etcifrede tal.

Strategier for addition

Forskning peger på, at elever generelt udvikler strategier til addition og subtraktion af etcifrede tal i en bestemt progression. For begge regningsarter består progressionen af tre typer af strategier.

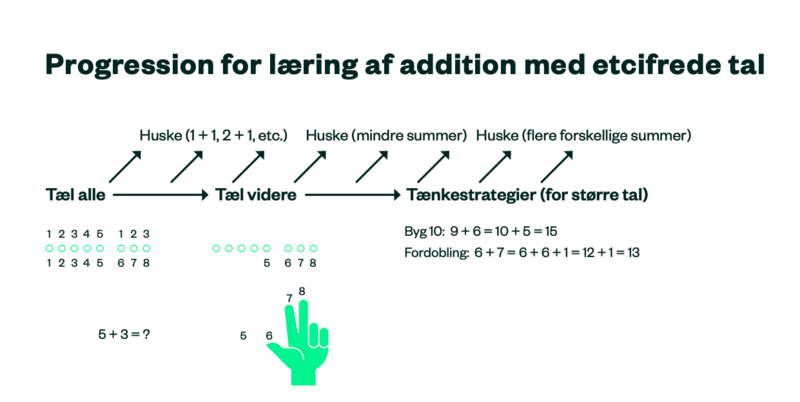
For addition er de tre strategier:

  1. Tæl-alle-strategi
  2. Tæl-videre-strategi
  3. Tænkestrategier
    (    Kilde 1 og 2)

Forskning tyder på, at det er muligt for næsten alle elever at komme til at udvikle tænkestrategier. For nogle elever kan det føles som om, at de gennemgår udviklingen næsten på egen hånd, når de bruger tal i forskellige sammenhænge. For andre elever - de fleste - foregår udviklingen ikke af sig selv, de er afhængige af lærerens støtte.

De fleste elever vil gennemgå udviklingen hurtigere, hvis de bliver undervist direkte i strategierne. Det er imidlertid helt afgørende, at undervisningen bygger på forståelse af strategierne og ikke alene på imitation og repetition af regler. (Kilde 1). Samtidig er det særdeles vigtigt, at læreren har en særlig opmærksomhed på elever, der i løbet af første klasse ikke begynder at bruge tænkestrategier, da der er en risiko for, at de ender i matematikvanskeligheder.

Forskning viser, at elever i høj grad bygger de efterfølgende strategier til regning med flercifrede tal på de strategier, de bruger til etcifrede tal, og at fokus på progression gennem de tre faser i de første skoleår er særdeles befordrende for, at eleverne kan udvikle fleksible strategier til beregninger med flercifrede tal (Kilde 2) og til algebraisk tænkning (Kilde 3).

Sideløbende med udviklingen af strategier er der en bevægelse fra, at eleverne arbejder med hverdagsproblemer til, at de regner abstrakt i deres hoved evt. med brug af notater. Det vil sige, at de går fra at bruge fingrene, centicubes eller andre konkrete hjælpemidler til at modellere problemerne til, at de efterhånden kan ’tænke i og med’ tal og regneudtryk og dermed regne ved at støtte sig til tal og regneudtryk og evt. noter og tegnede skitser.

Tællestrategier for addition

De fleste elever kender allerede ved skolestart resultatet af enkelte additionsstykker som fx $1+1$ og $1+24$, så her vil de oftest ikke foretage en beregning, men blot sige resultatet. Addition af større etcifrede tal udfører eleverne ved beregning, som i starten bygger på elevernes færdigheder i at tælle.

De fleste elever vil veksle mellem forskellige strategier og konkrete eller abstrakte metoder, afhængigt af konteksten og regnestykkets sværhedsgrad. Oftest vil elever ’gå et skridt tilbage’ og bruge en mere simpel metode eller strategi, når sværhedsgraden øges.

Tæl-alle-strategi

I starten adderer eleverne typisk $5+3$ ved først at finde og tælle $5$ klodser, så $3$ klodser og til sidst at tælle alle klodserne forfra (se figur 1).

Illustration: Progression for læring af addition med étcifrede tal
Figur 1: Progression for læring af addition med étcifrede tal - Bearbejdet efter Kilde 3 (s. 187)

Fra tæl-alle-strategi til tæl-videre-strategi

Ved en tæl-videre-strategi vælger eleven den ene addend (ideelt set den største) og tæller videre med den anden addend.

De to strategier og overgangen fra det konkrete til det abstrakte er beskrevet i nedenstående tabel ud fra følgende eksempel:

EKSEMPEL: Oliver har 5 guldfisk. Han får 3 nye guldfisk. Hvor mange guldfisk har Oliver nu?

(Bearbejdet efter Kilde 4)

Undervisningseksempler til tæl-videre strategi

I det følgende præsenteres fem aktiviteter, som kan støtte eleverne til at udvikle tæl-videre-strategi ud fra tæl-alle-strategi. (Eksemplerne er taget fra Kilde 4 og 5). Aktiviteterne er velegnede til elever, der bruger tæl-alle-strategi, typisk elever i 0. klasse og eventuelt i starten af 1. klasse.

Partner-tælleleg

Eleverne er sammen i par. Den ene starter med at tælle fra et og stopper ved et tilfældigt tal. Herefter tæller makkeren videre til et nyt, tilfældigt tal. Eleverne skiftes til at tælle videre, indtil de når fx 100.

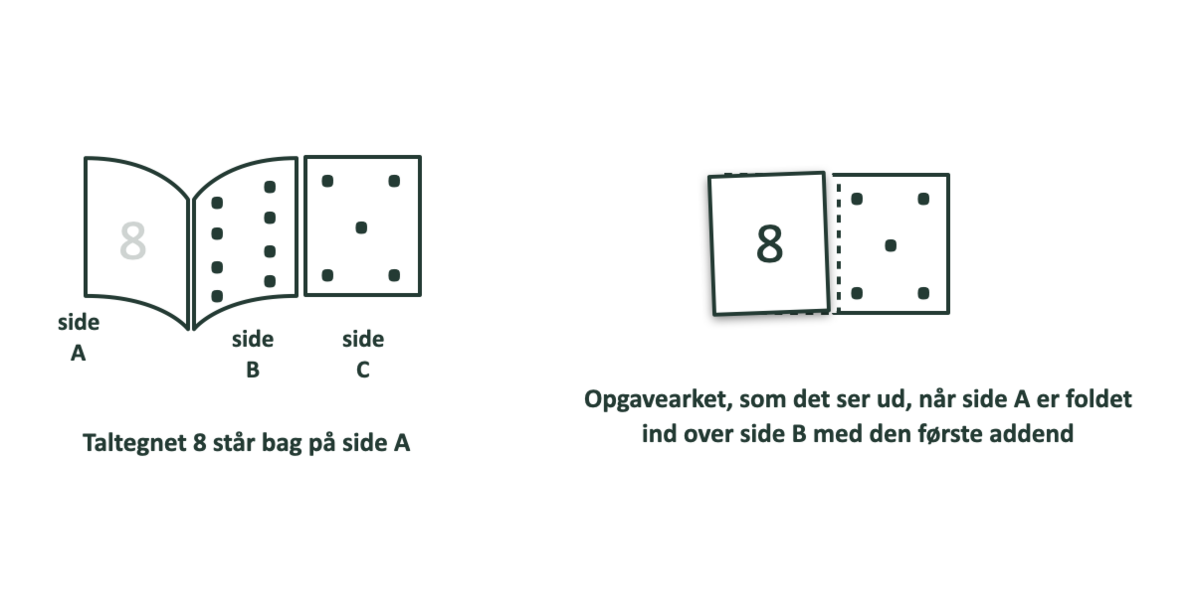
Skjulte prikker

Eleverne arbejder i par med additionsopgaver, hvor de to addender er repræsenteret med prikker. Papiret med opgaverne kan foldes i tre dele, så de prikker, der repræsenterer den ene addend, dækkes (se figur 2).

Illustration af foldeark beskrevet i eksemplet
Figur 2: Foldeark til addition - Bearbejdet fra kilde 5

Læreren demonstrerer for eleverne, at de skal folde papiret, så (fx) ottetallet dækker de otte prikker og derefter tælle videre på prikkerne til højre: ’Ni, ti, elleve, tolv, tretten’. På den måde finder de ud af, hvor mange prikker der er i alt.

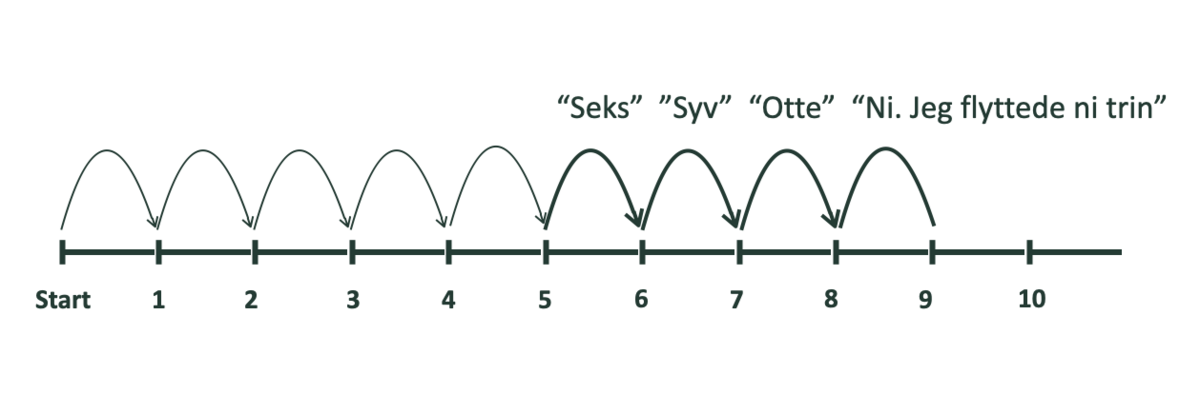
Tallinjen

En elev kaster en terning og hopper det antal, terningen viser (fx 5) på en tallinje på gulvet: ’En, to, tre, fire, fem’. Herefter slår eleven igen med terningen (fx 4) og hopper frem på tallinjen samtidig med, at han/hun tæller højt videre fra det første tal: ’Seks, syv, otte, ni’ (se figur 3) og viser en finger for hvert tal, han/hun tæller (4 i alt).

Illustration af tallinje beskrevet i eksemplet
Figur 3: Addition på tallinje. Bearbejdet fra kilde 5.

To terninger

Illustration: Terninger

Eleven slår med to terninger. På den ene terning er tallene fra 0 til 5 (eller fra 4 til 9), og på den anden er der fra 0 til 5 prikker (eller fra 4 til 9 prikker).  Eleven skal lægge tallet på den ene terning sammen med antallet af prikker på den anden terning (fx 5 og fire prikker) ved at tælle videre fra terningen med tallet 5: ‘Fem’. ’Seks, syv, otte, ni’.

Hvor mange er 3 flere end 6?

Eleverne skal svare på spørgsmål, som er formuleret på formen: ’Hvor mange er 3 flere end 6?’. Først skal de svare ved (konkret) at tælle videre: ’Seks. Syv (viser en finger), otte (viser to fingre), ni (viser tre fingre) - 9’, og bagefter (abstrakt) ved at ’tælle tælletallene’: ’Seks. Syv er én mere, otte er to mere, ni er tre mere - 9’.

Fra tællestrategier til tænkestrategier

En tænkestrategi er en ’smart’ metode, eleven bruger til at beregne fx en sum. Tænkestrategier kan bygge på kendte resultater, regler i forhold til opdagelser af sammenhænge, som eleverne har været med til at udvikle samt elevernes ræsonnementer og argumentation.

Fx kan en elev regne $7+5$ ved at opdele $5$ i $3+2$, fordi eleven kender tier-vennerne $7$ og $3$, og derfor ved, at $7+3=10$:

$7+5=7+(3+2)=(7+3)+2=10+2=12$

Når eleverne arbejder med hverdagsproblemer, der er knyttet til addition og subtraktion af etcifrede tal, vil de gøre forskellige ’opdagelser’, som er forbundet med centrale egenskaber ved tallene og regningsarterne. Læreren kan ’bringe opdagelserne frem i klassen’, og klassen kan i fællesskab formulere opdagelserne. Det kan fx være den kommutative lov (fx $4+3=3+4$), ’læg-0-til’ (giver tallet selv) og ’læg-1-til’ (giver næste tal i talrækken). (Kilde 4 og 2)

Opdagelserne er udgangspunktet for udvikling af tænkestrategier. Nogle opdagelser er særligt vigtige i den sammenhæng. To sådanne opdagelser er fremhævet i forskningen. Den ene er, at tallene (ofte med fordel) kan opdeles i forbindelse med beregninger – især hvis opdelingerne gør, at $10$ bliver en ’mellemstation’ i beregningerne. Den kan kaldes byg-10-strategien. Den anden er, at man i nogle beregninger med fordel kan bruge fordoblinger. Den kan kaldes brug fordobling strategien.

Tænkestrategier for addition

Byg-10-strategi

Udvikling af byg-10-strategi bygger på, at eleverne lærer summerne på $10$ de såkaldte tier-venner: $1+9$, $2+8$ osv., udenad.

Byg-10-strategi forudsætter tre ting:

  1. At eleven kan huske tier-vennerne udenad.
  2. At eleven er fortrolig med at opdele ethvert tal mindre end $10$ i alle de mulige summer, fx $7$ i $1+6$, $2+5$ og $3+4$.
  3. At eleven har kendskab til reglen for $10+n$, fx $10+4=14$.
    (Kilde 2)

Det er vigtigt, at disse tre forudsætninger behandles indgående. Specielt punkt 3 er vanskeligere for danske elever end for elever i nogle andre lande, fordi de danske talord for tallene fra $11$ til $19$ ikke hjælper eleverne, som de gør på andre sprog. Mange danske elever tænker $15$ som en-fem i stedet for som ti-fem.

Eleverne kan anvende tier-venner i byg-10-strategi, hvor den ene addend opsplittes i to dele, så man opnår et par af tier-venner: Fx $8+5=8+(2+3)=(8+2)+3=10+3=13$.

Brug fordobling strategien

Brug fordobling strategi bygger på at kunne huske ‘fordoblingstal’, $2+2=4$, $3+3=6$ osv.

Ud fra fordoblingstallene kan eleverne udlede ’nær-fordobling’, fx $6+7$, hvor $7$ kan opdeles i $6+1$, hvorefter fordobling og læg-1-til giver $(6+6)+1=12+1=13$.

Strategien er særlig anvendelig ved de sværeste additionsstykker med de højeste tal, når addenderne er næsten lige store, fx. $9+8$, $8+7$ og $7+6$. Til gengæld kræver nogle stykker andre strategier mere avancerede 'kompenseringer' i forhold til brug-fordoblinger, fx $8+5=7+6=12+1$ eller $8+4=6+6=12$. Enkelte stykker, fx $9+4$, er ikke hensigtsmæssige at løse med brug-fordoblinger- strategien.

Valg af strategi

Mange danske lærebøger har fokus på tier-venner og byg-10-strategien. En af fordelene er, at byg-10-strategien kan bruges til alle additionsstykker, hvor summen er større end $10$. Strategien er desuden en vigtig forudsætning, når eleverne skal udvikle nye strategier for beregninger med flercifrede tal. Forskning i klasser, hvor der bruges meget tid på brug-fordoblinger- strategi tyder imidlertid på, at den i mange tilfælde er mere effektiv end byg-10-strategi. (Kilde 6)

For at kunne regne flydende, er det vigtigt, at eleverne råder over flere forskellige tænkestrategier, som de kan bruge fleksibelt, det vil sige, at de kan vælge en hensigtsmæssig strategi i en given situation. Det forudsætter, at de stifter bekendtskab med flere, forskelligartede strategier og regler, herunder både byg-10 og brug-fordoblinger. I enkelte tilfælde, fx når den ene addend er 1, 2 eller 3, eller ved subtraktion af to tal, hvor forskellen er 1, 2 eller 3, kan det være hensigtsmæssigt at bruge tællestrategier. Undervisningen skal således lede hen imod, at eleverne i stigende grad - men ikke altid - bruger tænkestrategier.  

Strategier for subtraktion

Udviklingen af effektive strategier til subtraktion ligner på mange måder den for addition. Også her er udgangspunktet tællestrategier.
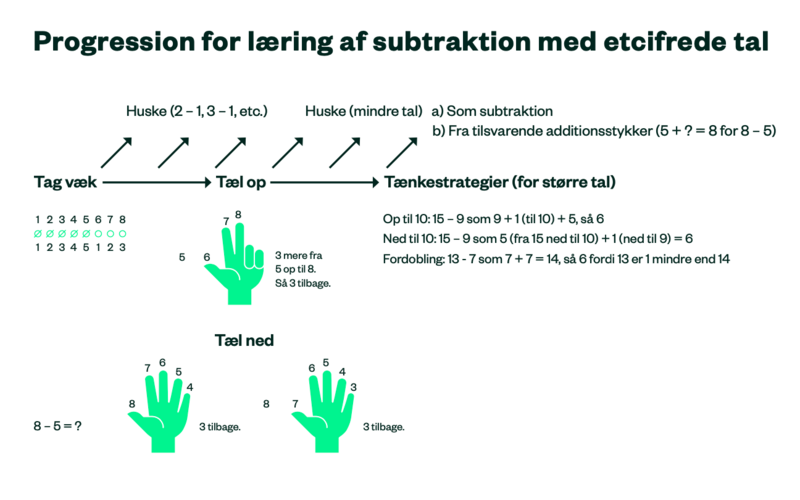
 For subtraktion er de tre strategier:

  1. Tag-væk-strategi
  2. Tæl-op-strategi
  3. Tænkestrategier
    (    Kilde 1 og 2)
Illustration: Progression for læring af subtraktion med étcifrede tal
Figur 4: Progression for læring af subtraktion med étcifrede tal - Bearbejdet efter Kilde 3 (s. 190)

Tællestrategier for subtraktion

Nogle elever anvender tæl-ned-strategi, men den har vist sig ofte at være svær og give anledning til hyppige fejl, især fordi eleverne kombinerer de to metoder, der er beskrevet under tæl-ned-strategi i figuren herover og får enten én for meget eller én for lidt. Det er desuden vanskeligt for mange elever at tælle baglæns. (Kilde 2)

Tæl-op-til strategi har til gengæld vist sig at være særdeles effektiv og endda lettere at lære for eleverne end tæl-videre strategien for addition. (Kilde  2)

Det er imidlertid afgørende, at eleverne introduceres for denne strategi tidligt, da de først sent eller måske slet ikke vil udvikle den af sig selv. I et amerikansk studie viste det sig, at alle elever, som havde arbejdet med tag-væk-strategien – også elever i matematikvanskeligheder – allerede i første klasse kunne lære at bruge tæl-op-til strategien ved subtraktion. (Kilde 2 )

Tænkestrategier til subtraktion

Lige som ved addition er de centrale tænkestrategier byg-10 og brug-fordobling (se figur 4). Herudover er sammenhængen mellem addition og subtraktion helt central, når eleverne skal udvikle strategier til subtraktion. De kan blandt andet opnå indsigt i denne sammenhæng ved, at der i undervisningen fokuseres på, hvilke situationer der kan løses med addition, og hvilke der kan løses med subtraktion. (Kilde 1)

’Subtraktion-som-addition-strategi’

Subtraktion-som-addition-strategi bygger på elevers forståelse af at beregne $9−4$ svarer til at finde ud af, hvilket tal man skal lægge til $4$, for at få $9$, altså $4+\_ =9$. Det stiller imidlertid krav om en fokuseret, meningsfuldt designet undervisning, for at give eleverne mulighed for at lære denne strategi. (Kilde 4)

Strategien forudsætter, at eleven har en grundlæggende forståelse af følgende fire sammenhænge:

  1. Addition og subtraktion ændrer størrelsen af en ’startværdi’, således at størrelsen bliver større ved addition og mindre ved subtraktion.
  2. Når man adderer en værdi og subtraherer den samme værdi, får man startværdien.
    Fx $7+4=11$ og $11−4=7$ ($7$ er startværdien).
  3. Addition og subtraktion er modsatte regningsarter. Hvis $a+b=c$, så er $c−b=a$ (og omvendt).
  4. Additions- og subtraktionsstykker deler de samme tre tal. Fx $7+4=11$, $11–7=4$ og $11–4=7$.

De fire sammenhænge kan også tænkes i en del + del = helhed kontekst. (Kilde 4)

Læs også: Regning med encifrede tal: Færdigheder og forståelse

Undervisningseksempler til tænkestrategier til addition og subtraktion

I det følgende præsenteres tre aktiviteter til tænkestrategier til beregninger med etcifrede tal (eksemplerne er taget fra kilde 7). Aktiviteterne er velegnede til 1. og 2. klassetrin.

Summer af 10

Eleverne er sammen to og to. Hvert par får 10 brikker (fx lavet af karton), hvor de to sider har hver sin farve, fx sort og hvid.

  1. Begge elever skal gætte, hvor mange brikker, der lander med den sorte side opad.
  2. Brikkerne kastes op i luften, så de lander på bordet.
  3. Eleverne tæller efter, om deres gæt var rigtige.
  4. Eleverne skal gætte, hvor mange brikker der landede med den hvide side opad.
  5. Eleverne tæller efter, om deres gæt var rigtige.

Prøv flere gange for at undersøge, hvilke summer der er.

Udfordring: Hvor mange forskellige muligheder er der? Hvordan kan I være sikre på, at I har fundet alle sammen.

Aktiviteten kan også udføres med 20 brikker.

Dobbelt-bingo

Hver elev får et blankt bingokort med 3 x 3 felter og et antal brikker til at dække felterne.

Hver elev skal skrive et lige tal mellem 2 og 20 i hvert felt. De må gerne skrive samme tal flere gange.

  1. Tag en spinner med tal fra 1 til 10 (eller en 10-sidet terning). Spin og sig tallet.
  2. Hvis eleven har det tal, der er det dobbelte af det tal, spinneren viser, placerer eleven en brik over tallet.
    Læreren kan ind imellem bede en elev om at argumentere for, at elevens tal er det dobbelte af det tal, spinneren viser eller spørge, hvordan eleven fandt ud af det.
  3.  Den elev, der først har markeret alle tal på pladen, har vundet.

Variationer

Halveringsbingo. Eleverne skriver tal mellem 1 og 10 på pladen. Læreren bruger en spinner med lige tal fra 2 til 20. Eleverne må placere en brik, hvis deres tal er det halve af tallet på spinneren.

Nær-dobbelt-bingo. Eleverne skriver ulige tal mellem 1 og 19 på pladen. Læreren bruger en spinner med tal fra 1 til 10. Eleverne må placere en brik, hvis deres tal er nær-dobbelt til tallet på spinneren. Hvis spinneren fx viser 6, kan eleverne både dække 13 og 11.  

To-mindre-bingo. Eleverne skriver tal mellem 5 og 20 på pladen. Læreren bruger en spinner med tal fra 7 til 22. Eleverne må placere en brik, hvis deres tal er to mindre end tallet på spinneren.

Summen er...

Læreren vælger et tal mellem 10 og 20, fx 13.

Eleverne skal finde to tal med summen 13.

Hvor mange forskellige summer, kan I finde?

Udfordring: Kan I finde 3 tal, med summen 13? 4 tal? …?

TIL OVERVEJELSE I FAGTEAMET

  • I hvor høj grad støtter jeres lærebogssystem elevernes udvikling af fleksibel brug af tænkestrategier i forhold til addition og subtraktion?
  • Hvor ser I de største udfordringer i forhold til, at eleverne udvikler en fleksibel brug af tænkestrategier til addition og subtraktion af etcifrede tal?
  • Giver denne tekst anledning til nogle overvejelser og eventuelle ændringer i den måde, I vil undervise i addition og subtraktion af etcifrede tal i fremtiden?
til: GRUNDSKOLE - Indskoling
emne: ALGEBRA
UDGIVET: 2022

Forfatter

Kaj Østergaard 

Lektor, ph.d.
VIA, Læreruddannelsen i Aarhus

Mere om temaet

Udgiver

Temaer på matematikdidaktik.dk udvikles i tæt samarbejde mellem forskere og praktikere og udgives af NCUM.
Se redaktionen og vores redaktionelle retningslinjer

Kilder

  1. Kilpatrick, J., Swafford, J. & Findell, B. (Eds.) (2001). Adding it up. Helping children learning mathematics. National Research Council. Washington, DC: National Academy Press.

  2. Fuson, K.C. (2003). Developing mathematical power in whole number operations. In J. Kilpatrick, W.G. Martin, & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 68–94). Reston, VA: National Council of Teachers of Mathematic

  3. Kaas, T. (2022). Tidlig algebra i grundskolens matematikundervisning.
  4. Baroody, A. J., & Purpura, D. J. (2017). Early number and operations: Whole numbers. In: J. Cai (Ed.), Compendium for Research in Mathematics Education, (pp. 308-354). Reston, VA: National Council of Teachers of Mathematics.
  5. Tzur, R., & Lambert, M. A. (2011). Intermediate participatory stages as zone of proximal development correlate in constructing counting-on: A Plausible Conceptual Source for Children's Transitory “Regress” to Counting-All. Journal for Research in Mathematics Education, 42(5), 418-450.
  6. Verschaffel, L., Greer, B. & De Corte, E. (2007). Whole number concepts and operations. I F. Lester (Ed.), Second handbook of research on mathematics teaching and learning, (pp. 555-628). Charlotte, NC: Information Age Publishing.
  7. Gervasoni, A. (2015). Extending Mathematical Understanding: Intervention. Ballarat Heritage Services Publishing

Mere om temaet

Del tema Print
Revideret 01.03.2024
-
Julie Fromholt-Iversen